Презентация на тему: Объёмы пространственных фигур

Объемы пространственных фигур 900igr.net

Вычисление объемов геометрических тел с помощью определенного интеграла.

1. Понятие объема 2. Объем прямой призмы 3. Объем цилиндра 4. Вычисление объемов тел с помощью определенного интеграла 5. Объем наклонной призмы 6. Объем пирамиды 7.Объем конуса 8. Объем шара 9. Объем шарового сегмента, шарового слоя, шарового сектора Содержание урока :

ОБЪЁМ. ЦЕЛИ УРОКА: Усвоить понятие объёма пространственной фигуры; Запомнить основные свойства объёма; Узнать формулы объёмов пространственных фигур. Раскрытие связи между двумя науками: алгеброй и геометрией. Вывод основной формулы для нахождения объёмов геометрических тел.

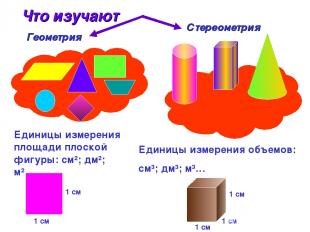
Геометрия Стереометрия Единицы измерения площади плоской фигуры: см²; дм²; м²… 1 см 1 см Единицы измерения объемов: см³; дм³; м³… 1 см 1 см 1 см Что изучают

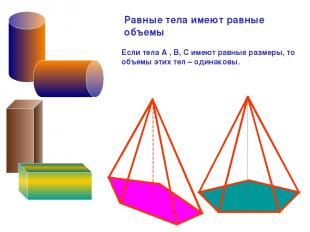
Равные тела имеют равные объемы Если тела А , В, С имеют равные размеры, то объемы этих тел – одинаковы.

Понятие объема в пространстве вводится аналогично понятию площади для фигур на плоскости. Определение 1.  Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами: равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется; если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей; за единицу объема принят объем куба, ребро которого равно единице длины; Определение 2.  Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V1 содержится внутри тела с объемом V2, то V1 

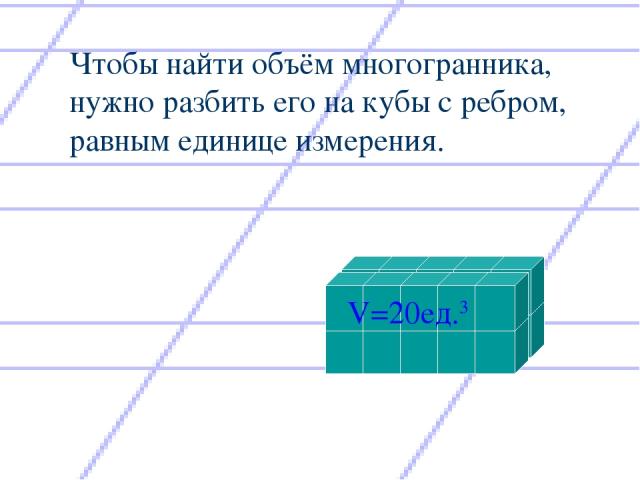
Чтобы найти объём многогранника, нужно разбить его на кубы с ребром, равным единице измерения. V=20ед.3

Если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей. V V=V1+V2 V1 V2 V

с а b V=abc Напомним формулу объёма прямоугольного параллелепипеда.

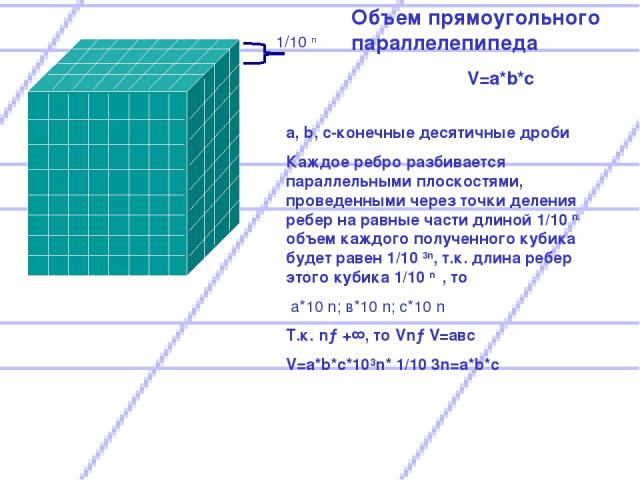
1/10 n Объем прямоугольного параллелепипеда V=a*b*c a, b, c-конечные десятичные дроби Каждое ребро разбивается параллельными плоскостями, проведенными через точки деления ребер на равные части длиной 1/10 n. объем каждого полученного кубика будет равен 1/10 3n, т.к. длина ребер этого кубика 1/10 n , то а*10 n; в*10 n; с*10 n Т.к. n→+∞, то Vn→V=авс V=a*b*c*10³n* 1/10 3n=a*b*c

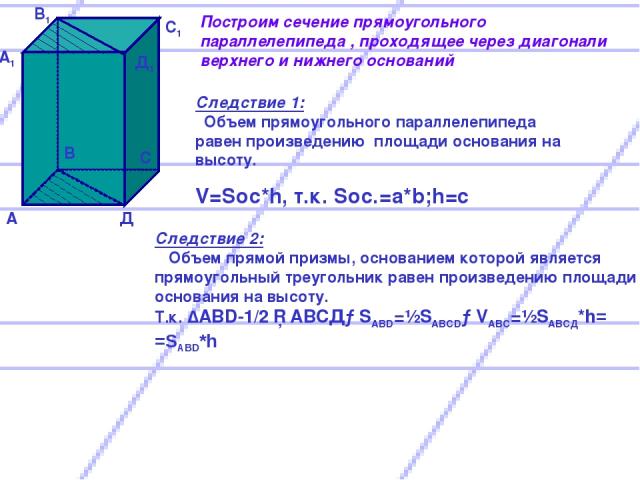
А А1 В В1 С С1 Д Д1 Следствие 1: Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. V=Soc*h, т.к. Sос.=a*b;h=c Следствие 2: Объем прямой призмы, основанием которой является прямоугольный треугольник равен произведению площади основания на высоту. Т.к. ∆ABD-1/2 □АВСД→SABD=½SABCD→VABC=½SABCД*h= =SABD*h Построим сечение прямоугольного параллелепипеда , проходящее через диагонали верхнего и нижнего оснований

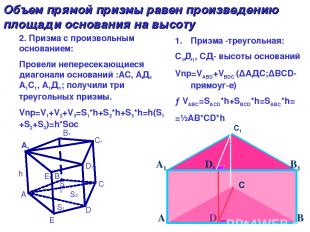
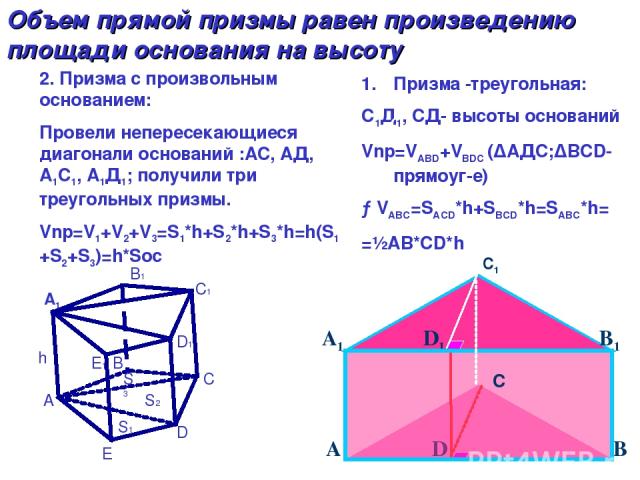
С1 Объем прямой призмы равен произведению площади основания на высоту Призма -треугольная: С1Д1, СД- высоты оснований Vnp=VABD+VBDC (∆AДC;∆BCD- прямоуг-е) →VABC=SAСD*h+SBCD*h=SABC*h= =½AВ*СD*h A E D C B h B1 C1 D1 E1 S1 S2 S3 2. Призма с произвольным основанием: Провели непересекающиеся диагонали оснований :АС, АД, А1С1, А1Д1; получили три треугольных призмы. Vnp=V1+V2+V3=S1*h+S2*h+S3*h=h(S1+S2+S3)=h*Soc А1 A D B A1 D1 B1 C1 С

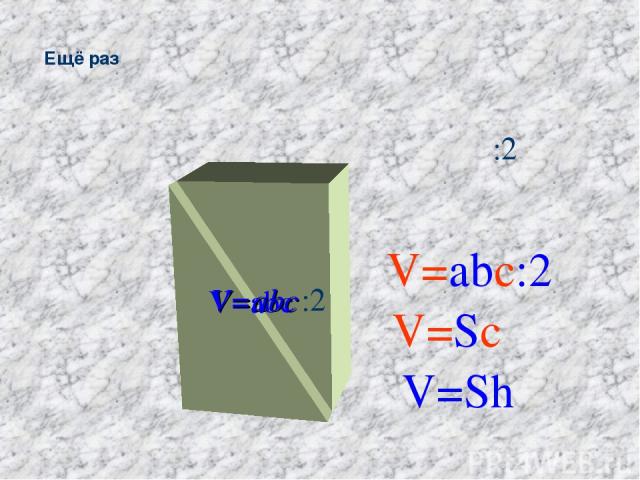
Ещё раз V=abc V=abc :2 :2 V=abc:2 V=Sc V=Sh

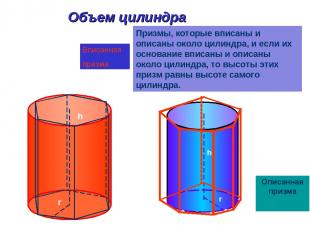
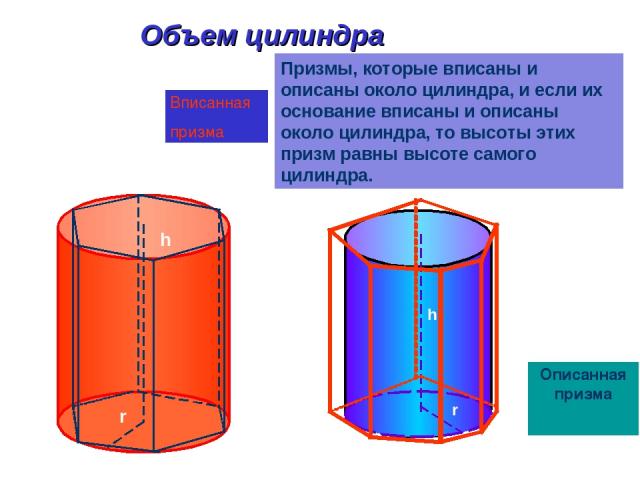
Объем цилиндра Призмы, которые вписаны и описаны около цилиндра, и если их основание вписаны и описаны около цилиндра, то высоты этих призм равны высоте самого цилиндра. h r h r Вписанная призма Описанная призма

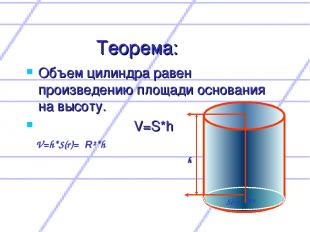
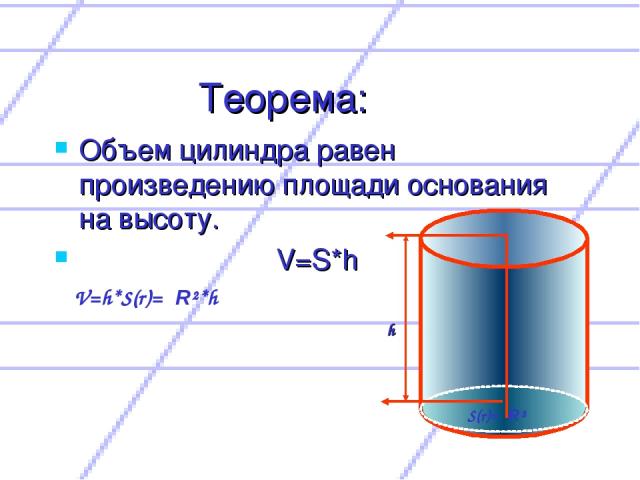
Теорема: Объем цилиндра равен произведению площади основания на высоту. V=S*h V=h*S(r)=πR²*h S(r)=πR² h

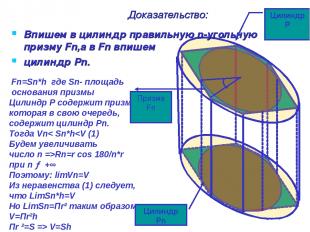
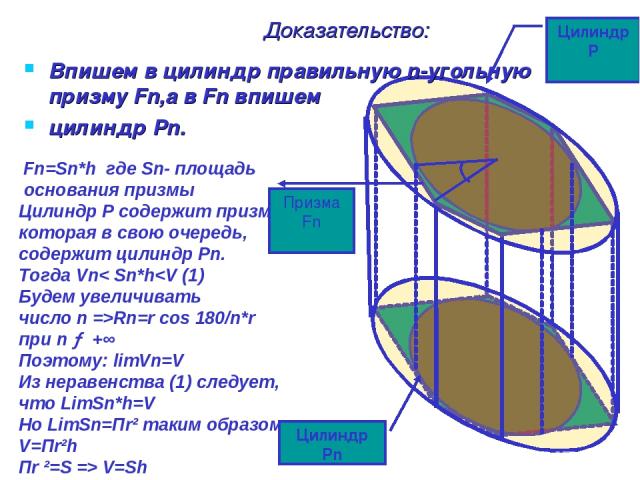
Доказательство: Впишем в цилиндр правильную n-угольную призму Fn,а в Fn впишем цилиндр Pn. Fn=Sn*h где Sn- площадь основания призмы Цилиндр Р содержит призму Fn, которая в свою очередь, содержит цилиндр Pn. Тогда Vn< Sn*hRn=r cos 180/n*r при n → +∞ Поэтому: limVn=V Из неравенства (1) следует, что LimSn*h=V Но LimSn=Пr² таким образом V=Пr²h Пr ²=S => V=Sh Цилиндр P Цилиндр Pn Призма Fn

Цели : Научиться применять интегрирование функций в качестве одного из способов решения задач на нахождение объёмов геометрических тел. Развитие логического мышления, пространственного воображения, умений действовать по алгоритму, составлять алгоритмы действий. Воспитание познавательной активности, самостоятельности.

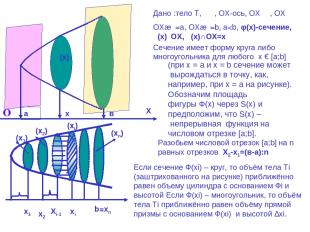
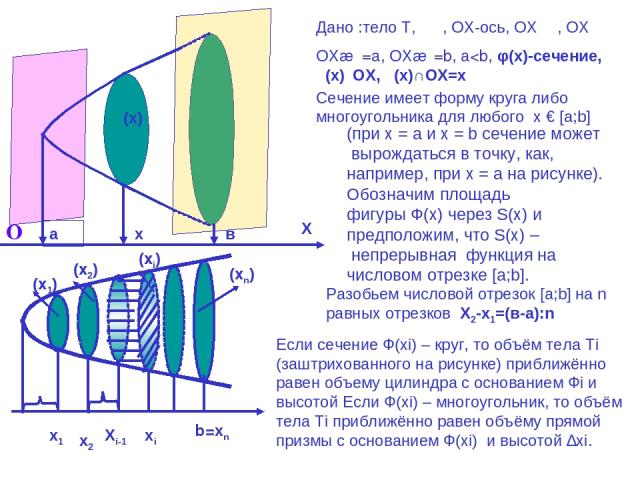
Дано :тело Т,αⅡβ, ОХ-ось, ОХ┴α, ОХ┴β ОХ∩α=a, ОХ∩β=b, а

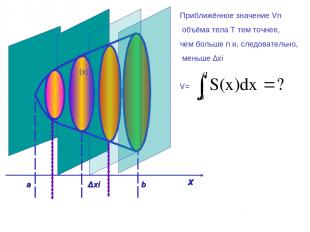
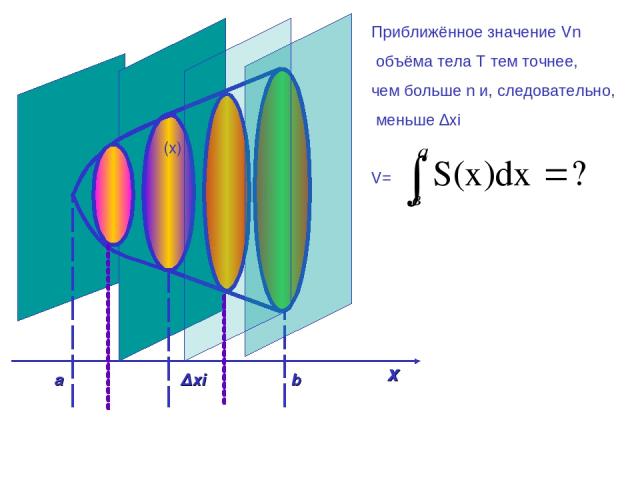
a ∆хі b х α β φ(x) Приближённое значение Vn объёма тела Т тем точнее, чем больше n и, следовательно, меньше ∆xi V=

A A1 A2 B B1 B2 C C1 C2 O X h X Объем наклонной призмы Объем наклонной призмы равен произведению площади основания на высоту Треугольная призма Т.п. имеет S основания и высоту h. O=OX∩(АВС); OXᅩ(АВС); (АВС)||(А1В1С1) ; (А1В1С1)-плоскость сечения: (А1В1С1) ᅩOX S(x)-площадь сечения; S=S(x), т.к. (АВС)||(А1В1С1) и ∆ABC=∆A1B1C1(АА1С1С-параллелограмм→АС=А1С1,ВС=В1С1, АВ=А1В1)

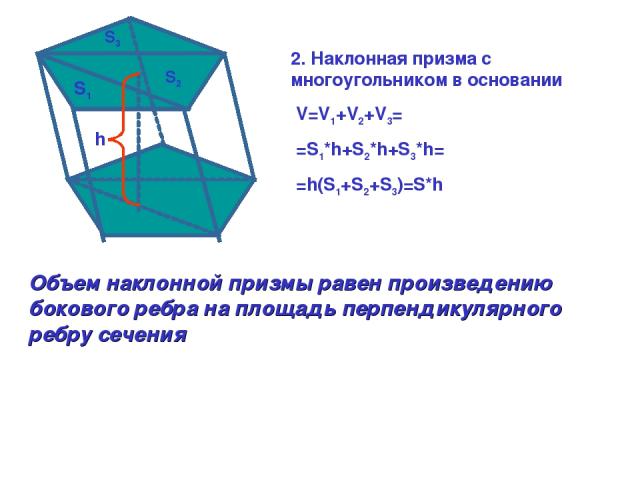
V=V1+V2+V3= =S1*h+S2*h+S3*h= =h(S1+S2+S3)=S*h S1 S2 S3 h Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ребру сечения 2. Наклонная призма с многоугольником в основании

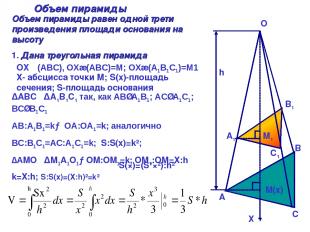
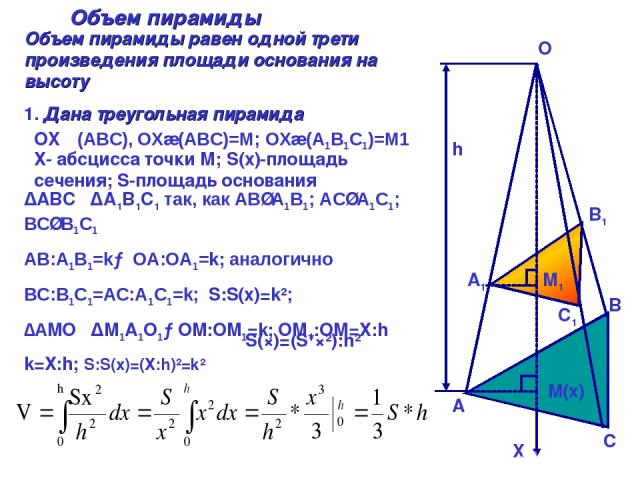
h A A1 B B1 C C1 M(х) M1 Объем пирамиды Объем пирамиды равен одной трети произведения площади основания на высоту 1. Дана треугольная пирамида O X OXᅩ(АВС), OX∩(АВС)=М; OX∩(A1B1C1)=М1 Х- абсцисса точки М; S(x)-площадь сечения; S-площадь основания ∆ABC∾∆A1B1C1 так, как АВ∥А1В1; АС∥А1С1; ВС∥В1С1 АВ:А1В1=k→ ОА:ОА1=k; аналогично ВС:В1С1=АС:А1С1=k; S:S(x)=k²; ∆AMO∾∆M1A1O1→OM:OM1=k; ОМ1:ОМ=Х:h k=Х:h; S:S(x)=(Х:h)²=k² S(×)=(S*ײ):h²

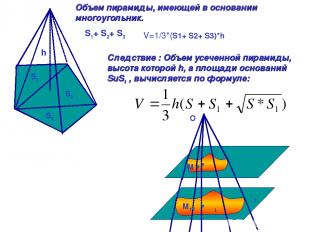
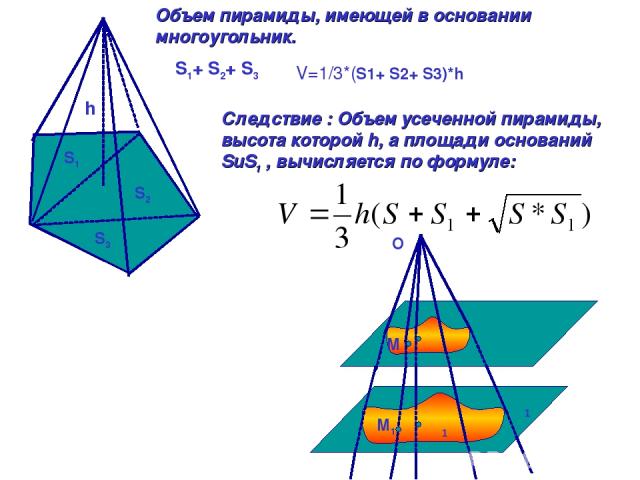
S1+ S2+ S3 S1 S2 S3 h V=1/3*(S1+ S2+ S3)*h Объем пирамиды, имеющей в основании многоугольник. Следствие : Объем усеченной пирамиды, высота которой h, а площади оснований SuS1 , вычисляется по формуле: α α1 φ φ1 М М1 O

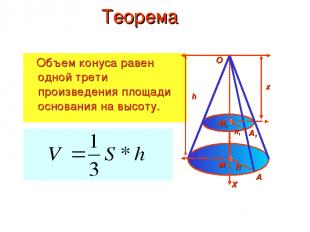
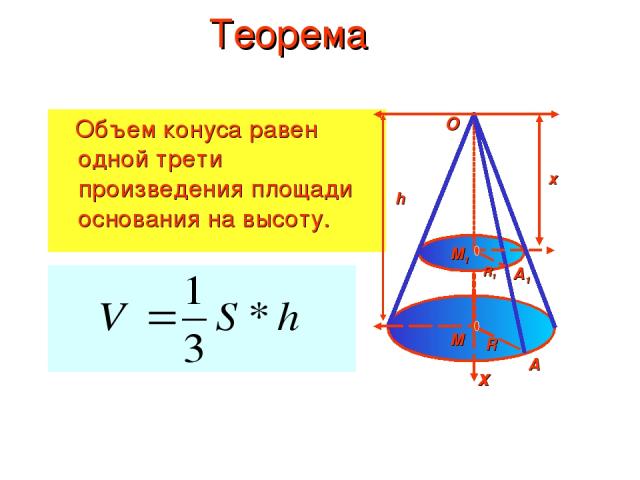
Теорема Объем конуса равен одной трети произведения площади основания на высоту. h х х O A A1 М М1 R R1

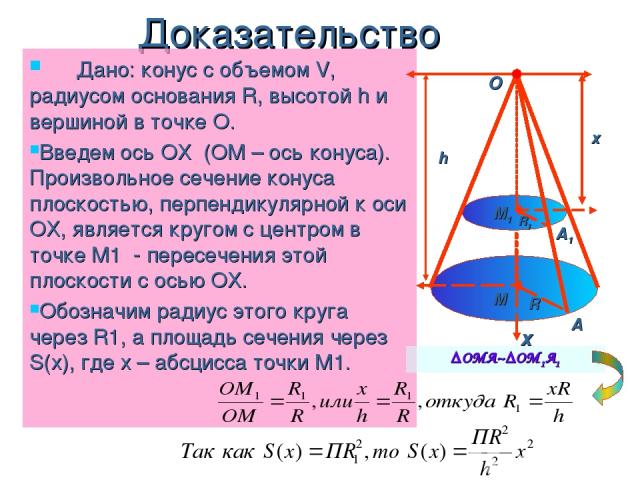
Доказательство Дано: конус с объемом V, радиусом основания R, высотой h и вершиной в точке О. Введем ось ОХ (ОМ – ось конуса). Произвольное сечение конуса плоскостью, перпендикулярной к оси ОХ, является кругом с центром в точке М1 - пересечения этой плоскости с осью ОХ. Обозначим радиус этого круга через R1, а площадь сечения через S(х), где х – абсцисса точки М1. h х х A A1 М М1 R R1 O ΔОМА~ΔОМ1А1

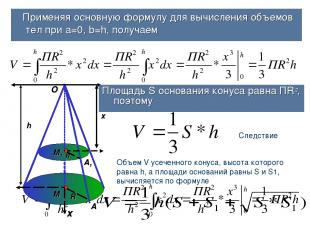
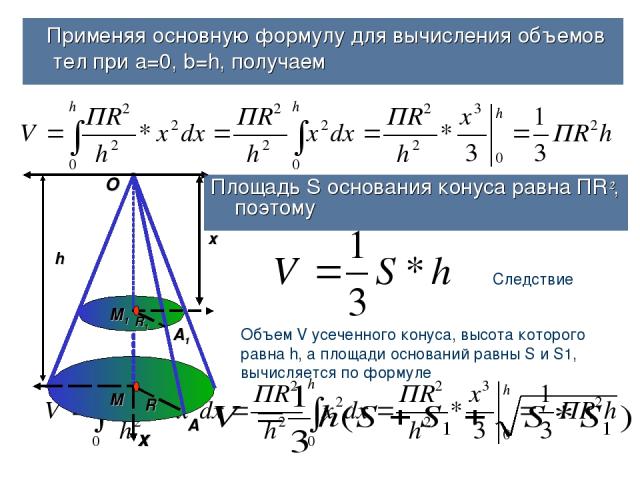
Применяя основную формулу для вычисления объемов тел при а=0, b=h, получаем h х х A A1 М М1 R R1 O Площадь S основания конуса равна ПR², поэтому Следствие Объем V усеченного конуса, высота которого равна h, а площади оснований равны S и S1, вычисляется по формуле

A М O C ⍶ х х Объем шара Теорема :Объем шара радиуса R равен 4/3πR³ Дано: шар, Rш ; О- центр шара; ОХ – ось шара; αᅩOX ;М- центр круга сечения; ОС=r; Sсеч. = S (x); х- абсцисса М Найти : V S (x)=πr² S (x)=π(R²-x²) -R≤ x ≤R Применяя основную формулу для вычисления объемов имеем :а =-R; b=R r R

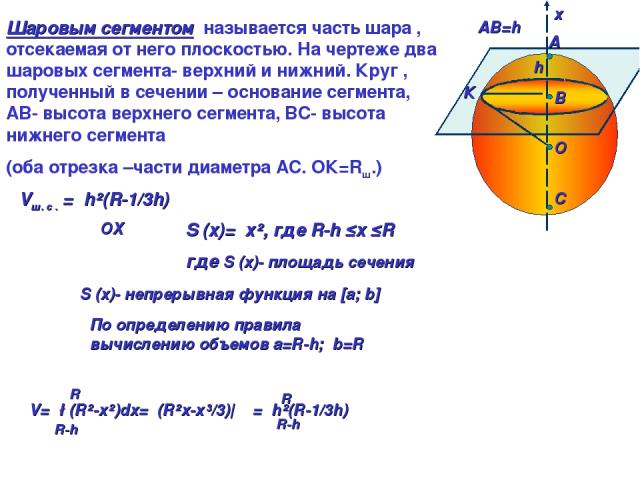
A B O C ⍶ АВ=h х Шаровым сегментом называется часть шара , отсекаемая от него плоскостью. На чертеже два шаровых сегмента- верхний и нижний. Круг , полученный в сечении – основание сегмента, АВ- высота верхнего сегмента, ВС- высота нижнего сегмента (оба отрезка –части диаметра АС. ОК=Rш.) К Vш. с . =πh²(R-1/3h) OX ￌ ⍶ S (x)=πх², где R-h ≤x ≤R где S (x)- площадь сечения V=π∫(R²-x²)dx=π(R²x-x³/3)| =πh²(R-1/3h) R R-h R-h R По определению правила вычислению объемов a=R-h; b=R S (x)- непрерывная функция на [a; b] h

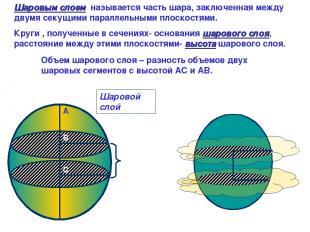
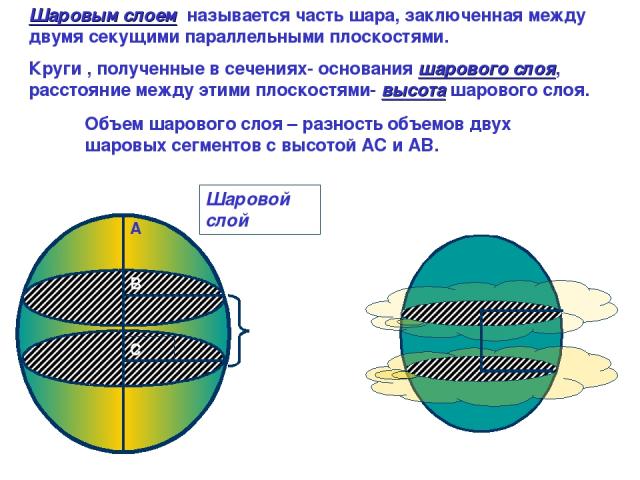
Шаровой слой A B C Шаровым слоем называется часть шара, заключенная между двумя секущими параллельными плоскостями. Круги , полученные в сечениях- основания шарового слоя, расстояние между этими плоскостями- высота шарового слоя. Объем шарового слоя – разность объемов двух шаровых сегментов с высотой АС и АВ.

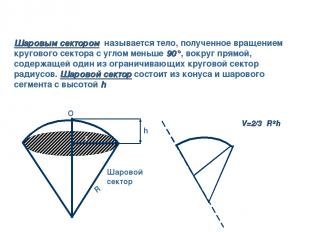
h R r O Шаровой сектор V=2/3πR²h Шаровым сектором называется тело, полученное вращением кругового сектора с углом меньше 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. Шаровой сектор состоит из конуса и шарового сегмента с высотой h