Презентация на тему: Объём тела вращения

Задачи по теме «Объемы тел вращения» Работу выполнил ученик 11 класса Кайгородцев Александр 900igr.net

Цель работы: Исследовать тела, полученные при вращении плоских фигур вокруг заданной оси. Задачи: Построение тел вращения, полученных при вращении различных фигур вокруг оси; Нахождение объема, полученного тела вращения в каждом случае.

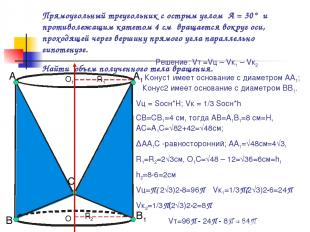
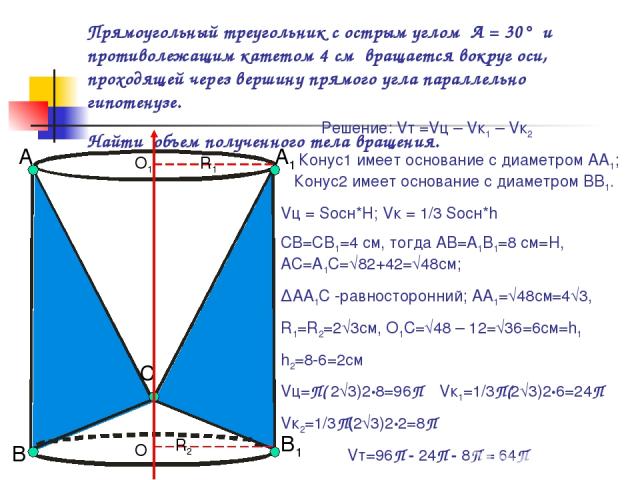
Прямоугольный треугольник с острым углом А = 30° и противолежащим катетом 4 см вращается вокруг оси, проходящей через вершину прямого угла параллельно гипотенузе. Найти объем полученного тела вращения. А В Решение: Vт =Vц – Vк1 – Vк2 Конус1 имеет основание с диаметром АА1; Конус2 имеет основание с диаметром ВВ1. Vц = Sосн*H; Vк = 1/3 Sосн*h СВ=СВ1=4 см, тогда АВ=А1В1=8 см=H, АС=А1С=√82+42=√48см; ∆АА1С -равносторонний; АА1=√48см=4√3, R1=R2=2√3см, О1С=√48 – 12=√36=6см=h1 h2=8-6=2см Vц=П( 2√3)2•8=96П Vк1=1/3П(2√3)2•6=24П Vк2=1/3П(2√3)2•2=8П Vт=96П - 24П - 8П = 64П Ответ: 64Псм3 А1 В1 С О О1 R1 R2

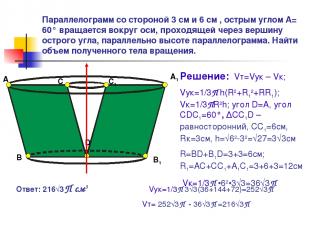
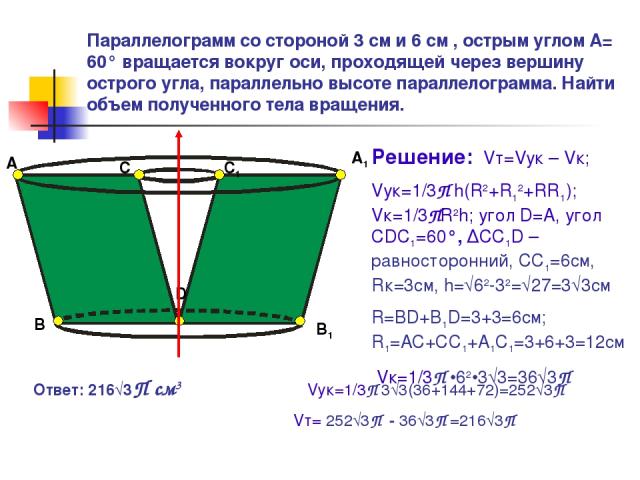
Параллелограмм со стороной 3 см и 6 см , острым углом А= 60° вращается вокруг оси, проходящей через вершину острого угла, параллельно высоте параллелограмма. Найти объем полученного тела вращения. А B C D С1 В1 А1 Решение: Vт=Vук – Vк; Vук=1/3П h(R2+R12+RR1); Vк=1/3ПR2h; угол D=A, угол СDC1=60°, ∆CC1D – равносторонний, СС1=6см, Rк=3см, h=√62-32=√27=3√3см R=BD+B1D=3+3=6cм; R1=AC+CC1+A1C1=3+6+3=12см Vк=1/3П •62•3√3=36√3П Ответ: 216√3П см3 Vук=1/3П 3√3(36+144+72)=252√3П Vт= 252√3П - 36√3П =216√3П

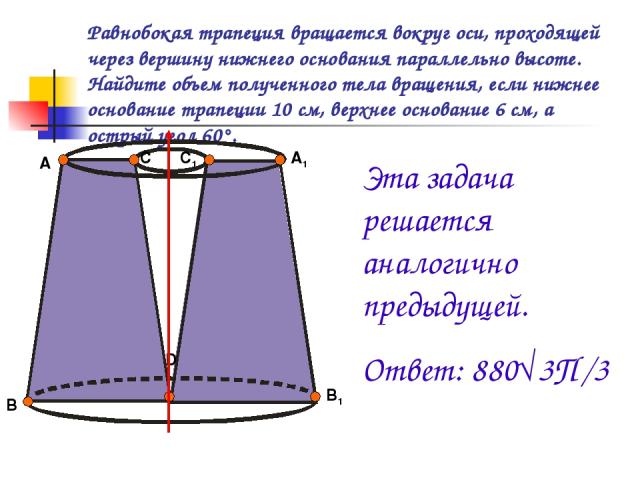
Равнобокая трапеция вращается вокруг оси, проходящей через вершину нижнего основания параллельно высоте. Найдите объем полученного тела вращения, если нижнее основание трапеции 10 см, верхнее основание 6 см, а острый угол 60°. А В С С1 А1 В1 D Эта задача решается аналогично предыдущей. Ответ: 880√3П /3

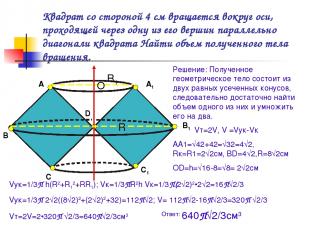
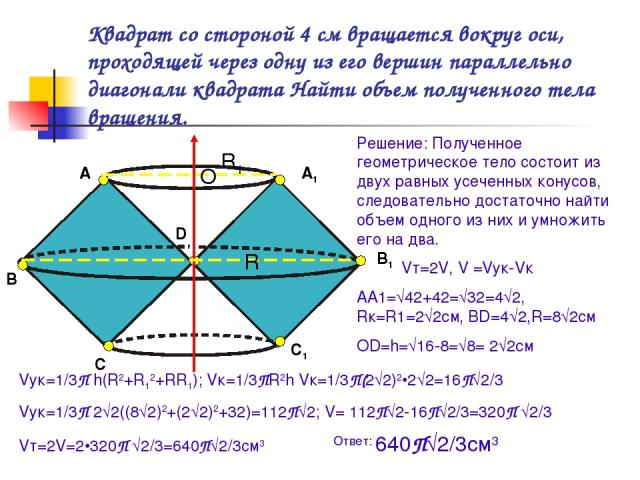
Квадрат со стороной 4 см вращается вокруг оси, проходящей через одну из его вершин параллельно диагонали квадрата Найти объем полученного тела вращения. А В С D А1 В1 С1 Решение: Полученное геометрическое тело состоит из двух равных усеченных конусов, следовательно достаточно найти объем одного из них и умножить его на два. Vт=2V, V =Vук-Vк AA1=√42+42=√32=4√2, Rк=R1=2√2cм, BD=4√2,R=8√2см OD=h=√16-8=√8= 2√2cм R1 R O Vук=1/3П h(R2+R12+RR1); Vк=1/3ПR2h Vк=1/3П(2√2)2•2√2=16П√2/3 Vук=1/3П 2√2((8√2)2+(2√2)2+32)=112П√2; V= 112П√2-16П√2/3=320П √2/3 Vт=2V=2•320П √2/3=640П√2/3см3 Ответ: 640П√2/3см3

Выводы: Вращаясь, плоские фигуры, вокруг заданной оси образуют известные тела вращения: цилиндр, усеченный конус, или комбинацию этих тел; Объемы полученных тел находятся вычислением объемов составляющих их тел и действий с ними.

Литература: Зив Б.Г. Дидактические материалы по геометрии для 11 класса. Москва, Просвещение, 2003 год; Цыпкин А.Г. Справочник по математике для средней школы. Москва, Просвещение 2000 год.