Презентация на тему: Неравенство треугольника

Неравенство треугольника Автор: Малышев Виктор Евгеньевич , Муниципальное образовательное учреждение средняя общеобразовательная школа № 21, 7 «В» кл. Научный руководитель: Синцова Татьяна Витальевна, учитель математики МОУ СОШ № 21 Российская Федерация, Костромская область, городской округ город Шарья Школьный конкурс «Шаг в будущее» Г. Шарья, 2009 год 900igr.net

Цели: углубить и расширить знания по теме неравенство треугольников. Задачи: разработать алгоритм решения задач; обучаться оформлению задач с использованием теоремы о неравенстве треугольников; научится решать задачи повышенной сложности.
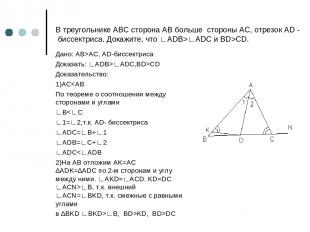
В треугольнике АВС сторона АВ больше стороны АС, отрезок AD - биссектриса. Докажите, что ∟ADB>∟ADC и BD>СD. Дано: AB>AC, AD-биссектриса Доказать: ∟ADB>∟ADC,BD>CD Доказательство: 1)ACKD, BD>DC
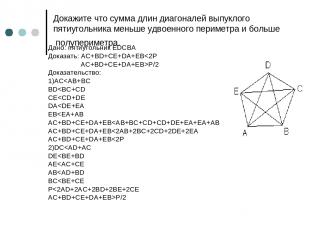
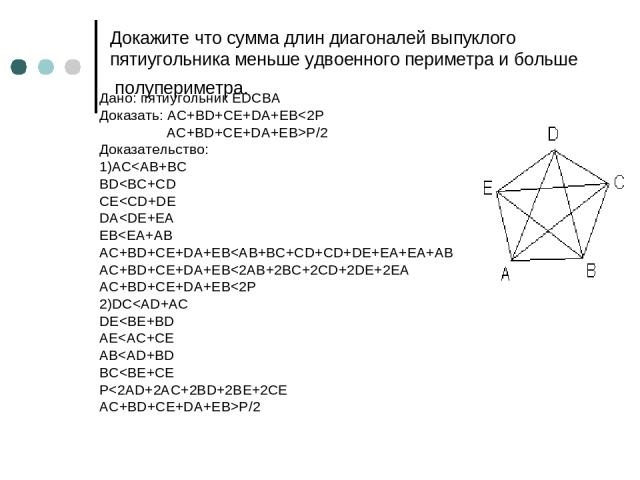
Докажите что сумма длин диагоналей выпуклого пятиугольника меньше удвоенного периметра и больше полупериметра. Дано: пятиугольник EDCBA Доказать: AC+BD+CE+DA+EBP/2 Доказательство: 1)AC

В целочисленном треугольнике (длины сторон которого являются целыми числами) длина одной из сторон равна 3, а периметр-18. Найдите длины двух других сторон треугольника. Дано: произвольный треугольник, P=18 Решение: 1) а +в>3 a + в=15 в=15-a 2) a+ в>3 a+3> в в+3>a 3) a+15-a>3 a+3>15-a 15-a+3>a 4)15>3 2a>12, a>6 -2a>-18, a6 a

Вывод: В ходе создания проекта я расширил свои знания по теме неравенство треугольников, отработал навыки оформления задач и повысил технику решения задач повышенной сложности на неравенство треугольников.