Презентация на тему: Задачи на неравенство треугольника

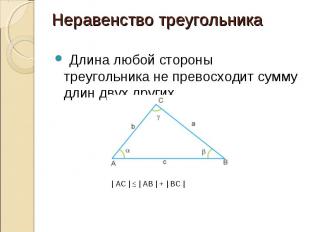
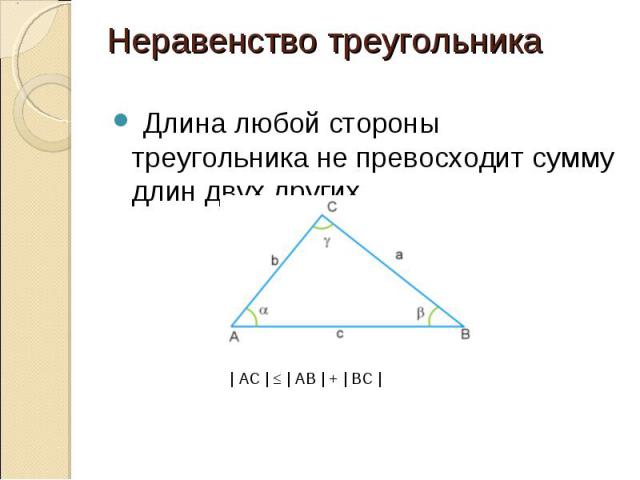
Длина любой стороны треугольника не превосходит сумму длин двух других Длина любой стороны треугольника не превосходит сумму длин двух других

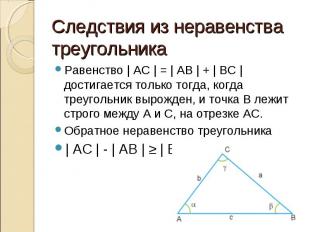
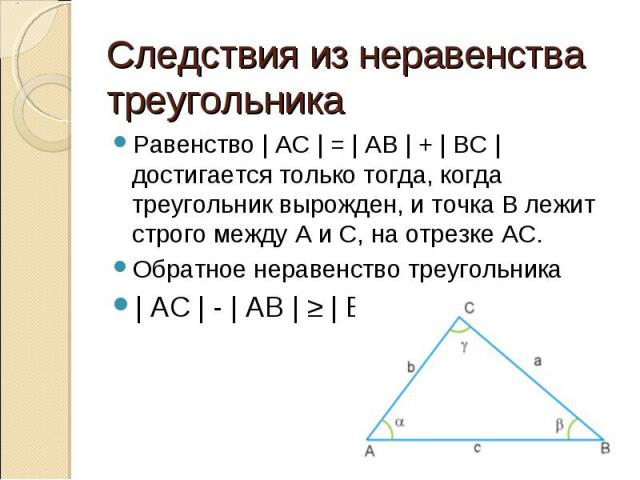
Равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C, на отрезке АС. Равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C, на отрезке АС. Обратное неравенство треугольника | AC | - | AB | ≥ | BC |

a, b, c – стороны треугольника, c – целое число. Найти c. a, b, c – стороны треугольника, c – целое число. Найти c. 1) а=8, b=6, с>12 2) a = 3,17, b = 0,75

РЕШЕНИЕ РЕШЕНИЕ 1) Из неравенства треугольника c < a+b, с< 8+6, с<14, по условию с>12. Т.к. с - целое число, оно равно 13. 2) Из неравенства треугольника c < a+b, с<3,17+0,75, с< 3,92; но из обратного неравенства треугольника c>a-b, т.е. с> 3,17-0,75, c>2,42. Т.к. с - целое число, оно равно 3.

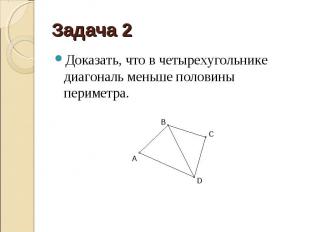
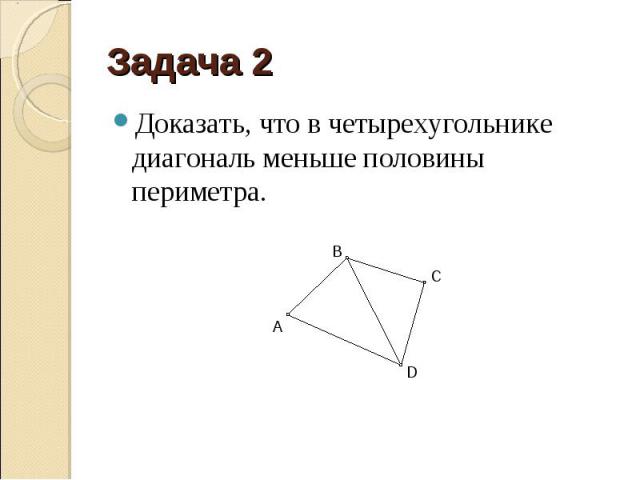
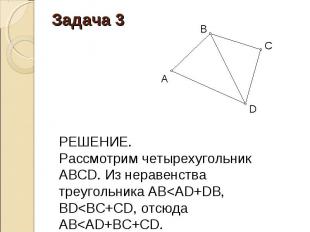
Доказать, что в четырехугольнике диагональ меньше половины периметра. Доказать, что в четырехугольнике диагональ меньше половины периметра.

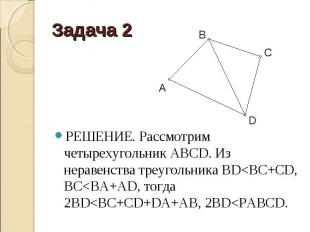
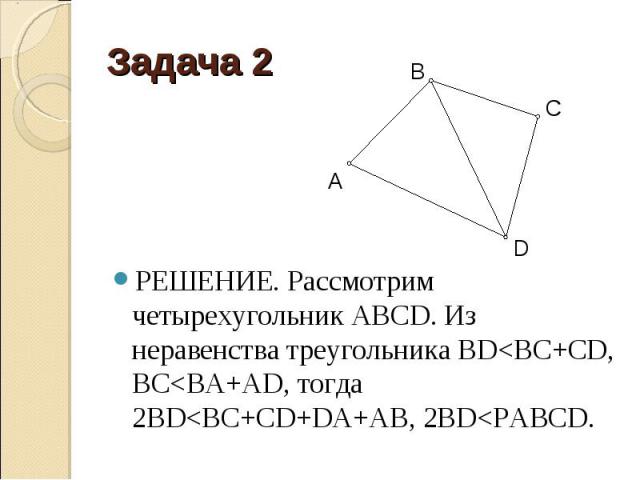
РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Из неравенства треугольника BD<BC+CD, BC<BA+AD, тогда 2BD<BC+CD+DA+AB, 2BD<PABCD.

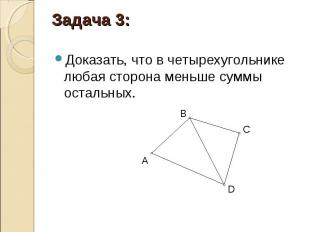
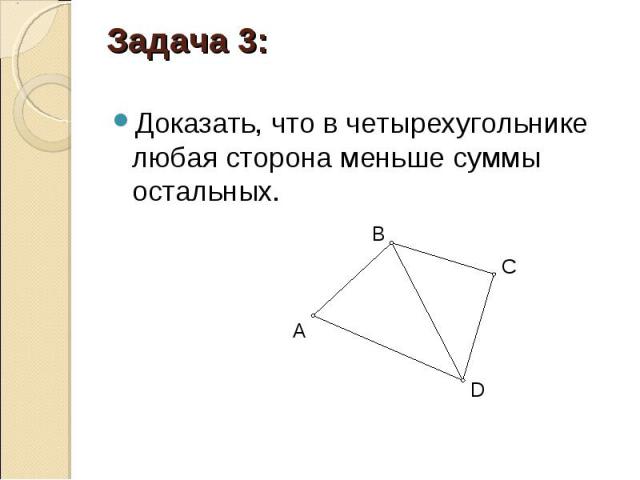
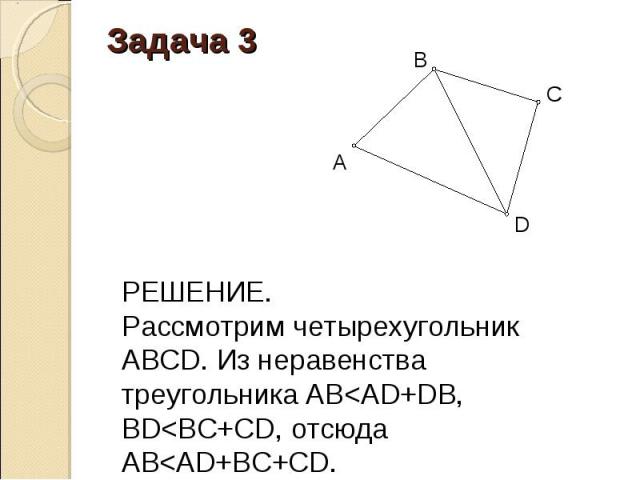
Доказать, что в четырехугольнике любая сторона меньше суммы остальных. Доказать, что в четырехугольнике любая сторона меньше суммы остальных.

М и Р – точки внутри четырехугольника. Доказать, что расстояние между ними меньше половины периметра четырехугольника. М и Р – точки внутри четырехугольника. Доказать, что расстояние между ними меньше половины периметра четырехугольника.

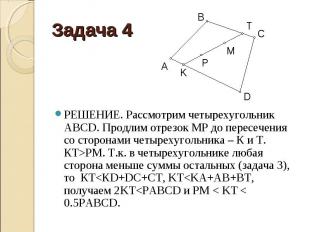
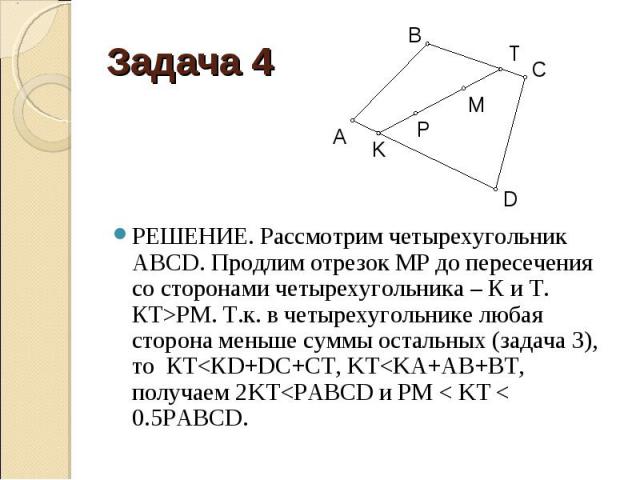
РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Продлим отрезок МР до пересечения со сторонами четырехугольника – К и Т. КТ>РМ. Т.к. в четырехугольнике любая сторона меньше суммы остальных (задача 3), то КТ<КD+DC+CT, KT<KA+AB+BT, получаем 2KT<PABCD и РМ < KT < 0.5PABCD. РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Продлим отрезок МР до пересечения со сторонами четырехугольника – К и Т. КТ>РМ. Т.к. в четырехугольнике любая сторона меньше суммы остальных (задача 3), то КТ<КD+DC+CT, KT<KA+AB+BT, получаем 2KT<PABCD и РМ < KT < 0.5PABCD.

Есть 7 прутьев длиннее 9 см, но короче 1 м. Доказать, что из трех из них можно составить треугольник. Есть 7 прутьев длиннее 9 см, но короче 1 м. Доказать, что из трех из них можно составить треугольник.

РЕШЕНИЕ. Предположим, что треугольник составить нельзя. Берем 2 самых коротких, их длина больше 9 см. Следующим должен быть больше 9 + 9 = 18 см, иначе можно составить треугольник. Четвертый больше 18 + 9 = 27, пятый больше 27 + 18 = 45, шестой больше 45 + 27 = 72, и последний будет больше 72 + 45 = 112, что больше метра. Получили противоречие. РЕШЕНИЕ. Предположим, что треугольник составить нельзя. Берем 2 самых коротких, их длина больше 9 см. Следующим должен быть больше 9 + 9 = 18 см, иначе можно составить треугольник. Четвертый больше 18 + 9 = 27, пятый больше 27 + 18 = 45, шестой больше 45 + 27 = 72, и последний будет больше 72 + 45 = 112, что больше метра. Получили противоречие.