Презентация на тему: Задачи 11 класс

Тема “Разные задачи на многогранники, цилиндр, конус и шар” является одной из самых сложных в курсе геометрии 11 класса. Тема “Разные задачи на многогранники, цилиндр, конус и шар” является одной из самых сложных в курсе геометрии 11 класса. В учебнике С.Атанасяна и др. по данной теме (стр. 138) можно найти только определения многогранника, описанного около сферы, многогранника, вписанного в сферу, сферы, вписанной в многогранник, и сферы, описанной около многогранника. В методических рекомендациях к этому учебнику (см. книгу “Изучение геометрии в 10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159) сказано, какие комбинации тел рассматриваются при решении задач № 629–646, и обращается внимание на то, что “при решении той или иной задачи прежде всего нужно добиться того, чтобы учащиеся хорошо представляли взаимное расположение указанных в условии тел”. Далее приводится решение задач №638(а) и №640. Учитывая все выше сказанное, и то, что наиболее трудными для учащихся являются задачи на комбинацию шара (сферы) с другими телами, необходимо систематизировать соответствующие теоретические положения и сообщить их учащимся.

Целью своего проекта ставлю: формирование устойчивого интереса к предмету геометрия, повышения качества знаний учащихся. Целью своего проекта ставлю: формирование устойчивого интереса к предмету геометрия, повышения качества знаний учащихся. Достижение обозначенной цели предполагает решение мной следующих задач: углубить знания по изучаемой теме; способствовать развитию познавательного интереса к предмету; расширить возможность визуализации учебного материала; развивать интеллектуальные способности учащихся.

Если школа не идет в ногу с жизнью, то учащиеся «перестают ее уважать, перестают ей верить. Когда учащиеся теряют доверие и уважение к школе, то учитель утрачивает авторитет и школа погрязает в проблемах плохой дисциплины и успеваемости». Если школа не идет в ногу с жизнью, то учащиеся «перестают ее уважать, перестают ей верить. Когда учащиеся теряют доверие и уважение к школе, то учитель утрачивает авторитет и школа погрязает в проблемах плохой дисциплины и успеваемости». Симур Паперт

Применение презентаций обеспечивает Применение презентаций обеспечивает получение большего объема информации за короткий период, всегда можно вернуться к предыдущему слайду ( обычная школьная доска не может вместить тот объем, который может вместить слайд); повышение плотности урока; привлечение и удержание внимания учащихся. Работа с презентациями заставляет учителя конкретизировать объемный материал, формулировать свои мысли предельно кратко и лаконично, систематизировать полученную информацию, представляя её в виде краткого конспекта.

Предисловие Предисловие Многогранники, вписанные в шар Основные определения и теоремы Вопросы Примеры решения задач Многогранники, описанные около шара Основные определения и теоремы Вопросы Примеры решения задач Комбинация шара с круглыми телами Вариант самостоятельной работы Заключение

Материал представлен по следующему плану: Материал представлен по следующему плану: основные теоретические сведения (могут быть предложены учащимся для записи, т. к. школьные учебники не содержат этих сведений); вопросы (используя их, учитель может провести опрос учащихся в устной форме); примеры решения задач (для организации классной и домашней работы учащихся). Как итог, приводится примерный текст самостоятельной работы, которую учитель может провести по окончании изучения данной темы. Тема "Комбинации тел" рассматривается как завершающая после изучения свойств многогранников и тел вращения, перед изучением формул объёмов.

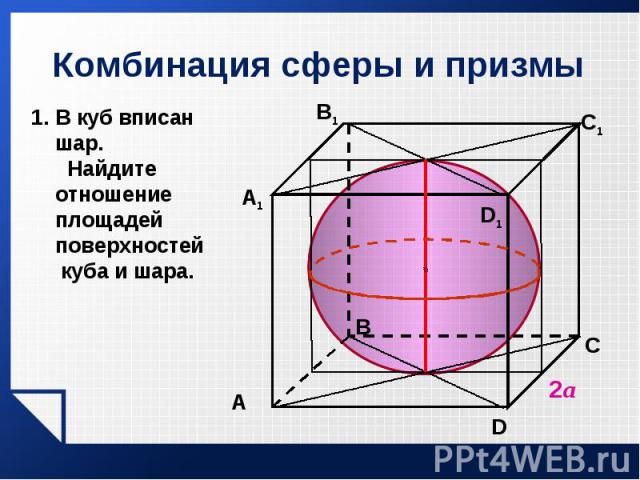
Можно ли описать сферу (шар) около: Можно ли описать сферу (шар) около: а) куба; б) прямоугольного параллелепипеда; в) наклонного параллелепипеда, в основании которого лежит прямоугольник; г) прямого параллелепипеда; д) наклонного параллелепипеда? При каких условиях можно описать сферу около призмы, в основании которой – трапеция? Каким условиям должна удовлетворять призма, чтобы около нее можно было описать сферу?

Около треугольной призмы описана сфера, центр которой лежит вне призмы. Какой треугольник является основанием призмы? Около треугольной призмы описана сфера, центр которой лежит вне призмы. Какой треугольник является основанием призмы? Можно ли описать сферу около наклонной призмы? При каком условии центр сферы, описанной около прямой треугольной призмы, будет находится на одной из боковых граней призмы? Около прямоугольного параллелепипеда, ребра которого равны 1 дм, 2 дм и 2 дм, описана сфера. Вычислите радиус сферы

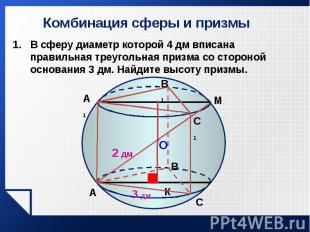
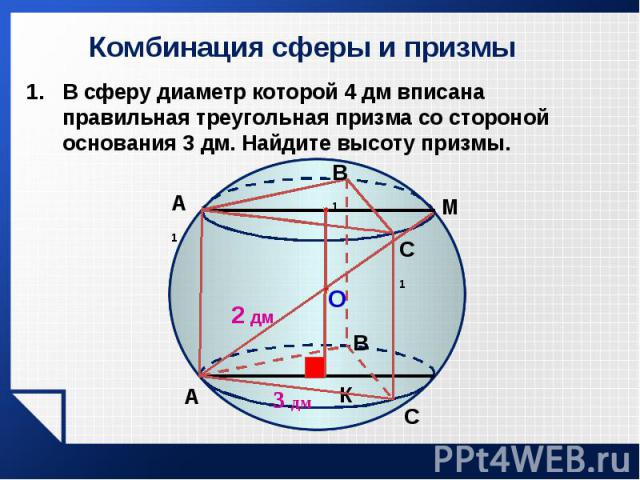
В сферу диаметр которой 4 дм вписана правильная треугольная призма со стороной основания 3 дм. Найдите высоту призмы. В сферу диаметр которой 4 дм вписана правильная треугольная призма со стороной основания 3 дм. Найдите высоту призмы.

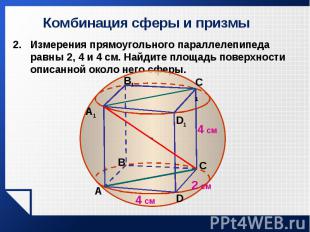
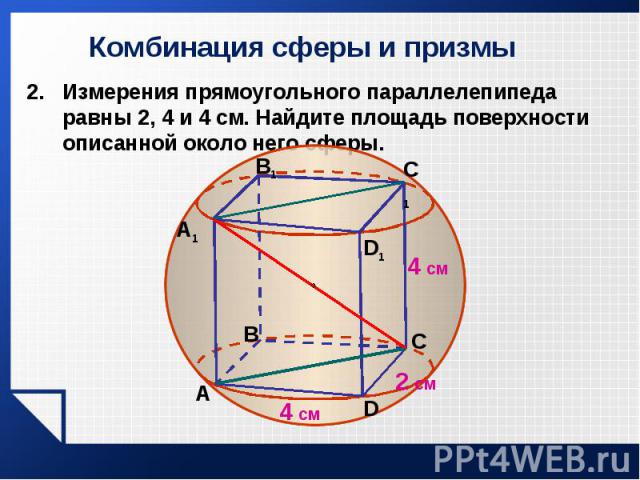
Измерения прямоугольного параллелепипеда равны 2, 4 и 4 см. Найдите площадь поверхности описанной около него сферы. Измерения прямоугольного параллелепипеда равны 2, 4 и 4 см. Найдите площадь поверхности описанной около него сферы.

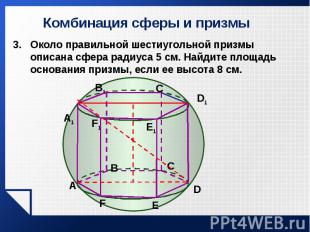
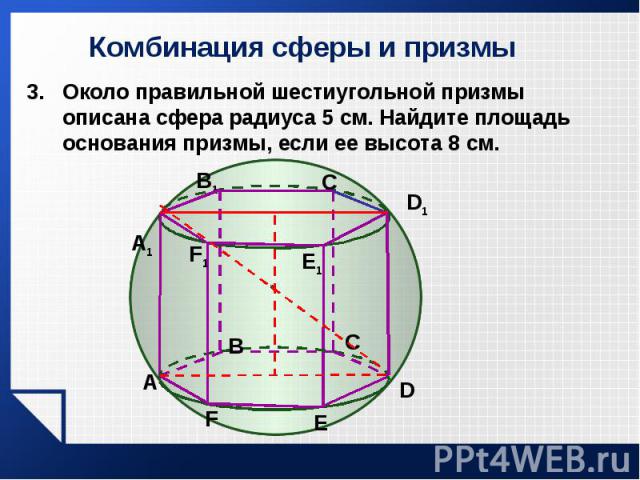
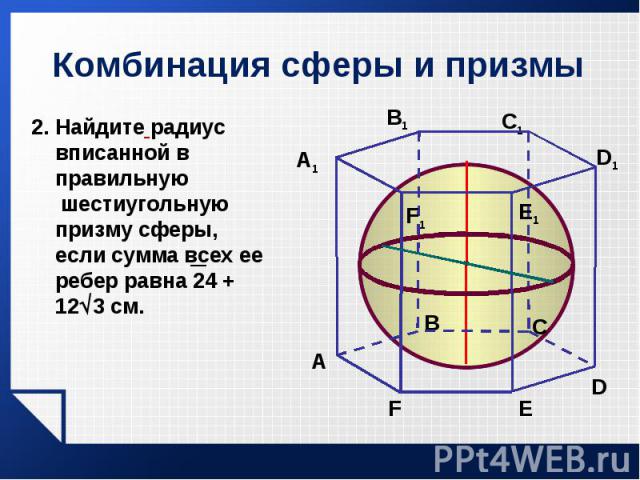
Около правильной шестиугольной призмы описана сфера радиуса 5 см. Найдите площадь основания призмы, если ее высота 8 см. Около правильной шестиугольной призмы описана сфера радиуса 5 см. Найдите площадь основания призмы, если ее высота 8 см.

Из учебника Л.С.Атанасяна № 637(а), №639(а,б) Из учебника Л.С.Атанасяна № 637(а), №639(а,б)

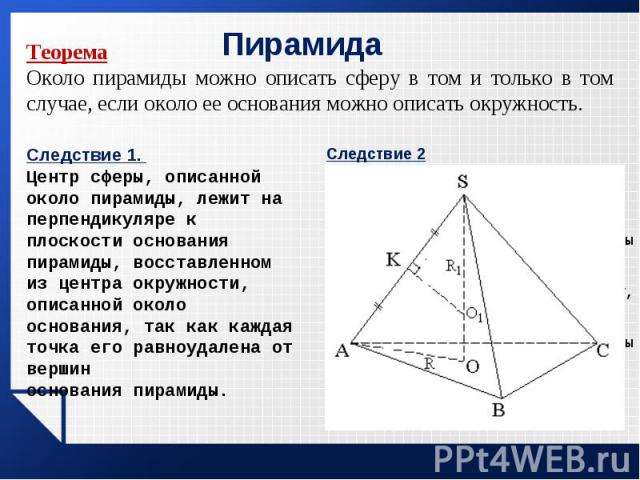
Справедливо ли утверждение, что около любой треугольной пирамиды можно описать сферу? Справедливо ли утверждение, что около любой треугольной пирамиды можно описать сферу? Можно ли описать сферу около любой четырехугольной пирамиды? Какими свойствами должна обладать пирамида, чтобы около нее можно было описать сферу? В сферу вписана пирамида, боковое ребро которой перпендикулярно основанию. Как найти центр сферы? Около правильной пирамиды описана сфера. Как расположен ее центр относительно элементов пирамиды?

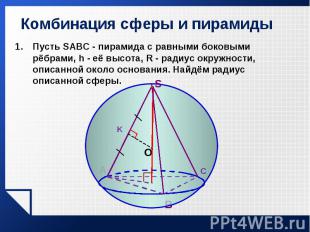
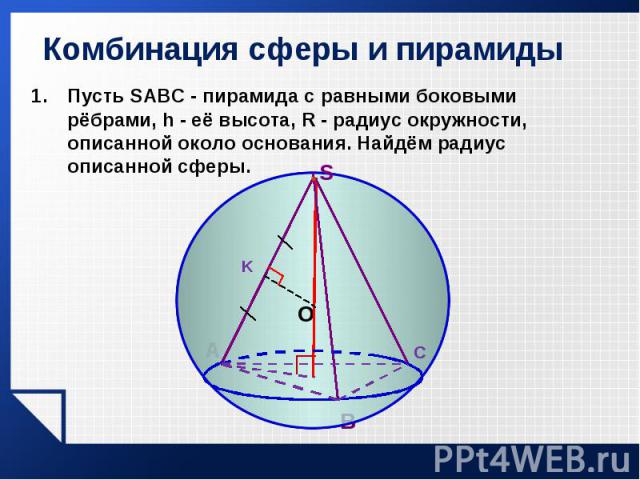
Пусть SABC - пирамида с равными боковыми рёбрами, h - её высота, R - радиус окружности, описанной около основания. Найдём радиус описанной сферы. Пусть SABC - пирамида с равными боковыми рёбрами, h - её высота, R - радиус окружности, описанной около основания. Найдём радиус описанной сферы.

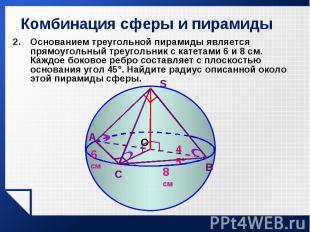
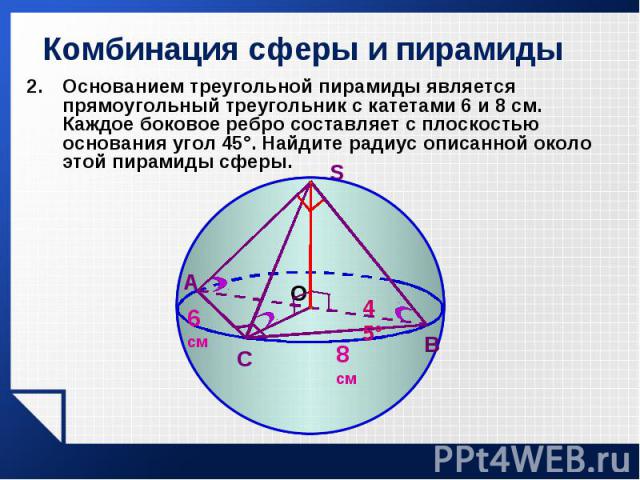
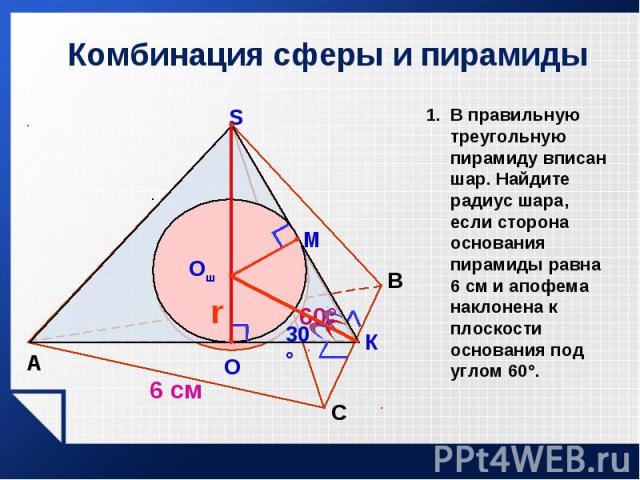
Основанием треугольной пирамиды является прямоугольный треугольник с катетами 6 и 8 см. Каждое боковое ребро составляет с плоскостью основания угол 45°. Найдите радиус описанной около этой пирамиды сферы. Основанием треугольной пирамиды является прямоугольный треугольник с катетами 6 и 8 см. Каждое боковое ребро составляет с плоскостью основания угол 45°. Найдите радиус описанной около этой пирамиды сферы.

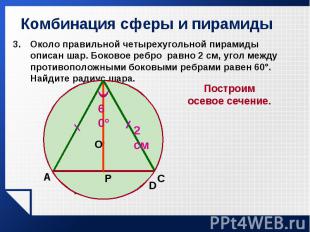
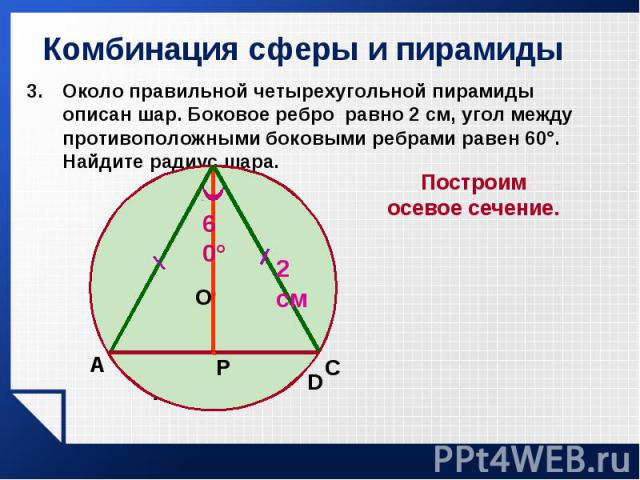
Около правильной четырехугольной пирамиды описан шар. Боковое ребро равно 2 см, угол между противоположными боковыми ребрами равен 60°. Найдите радиус шара. Около правильной четырехугольной пирамиды описан шар. Боковое ребро равно 2 см, угол между противоположными боковыми ребрами равен 60°. Найдите радиус шара.

Из учебника Л.С.Атанасяна № 637(б), №639(в) Из учебника Л.С.Атанасяна № 637(б), №639(в)

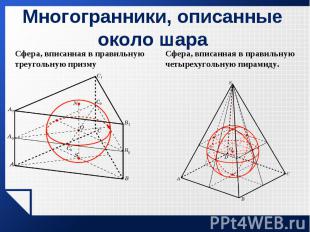
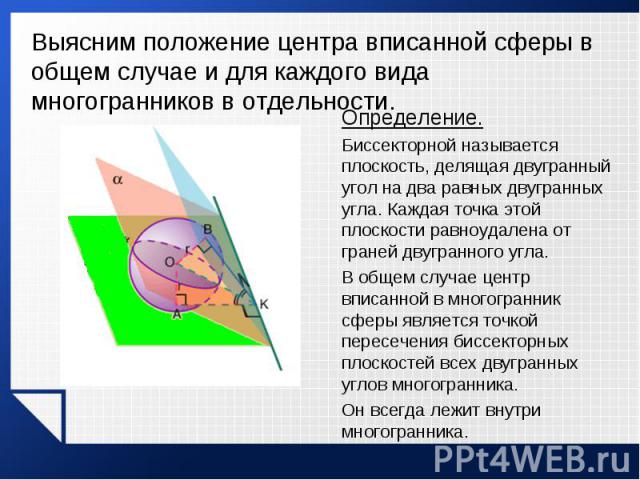
Определение. Определение. Биссекторной называется плоскость, делящая двугранный угол на два равных двугранных угла. Каждая точка этой плоскости равноудалена от граней двугранного угла. В общем случае центр вписанной в многогранник сферы является точкой пересечения биссекторных плоскостей всех двугранных углов многогранника. Он всегда лежит внутри многогранника.

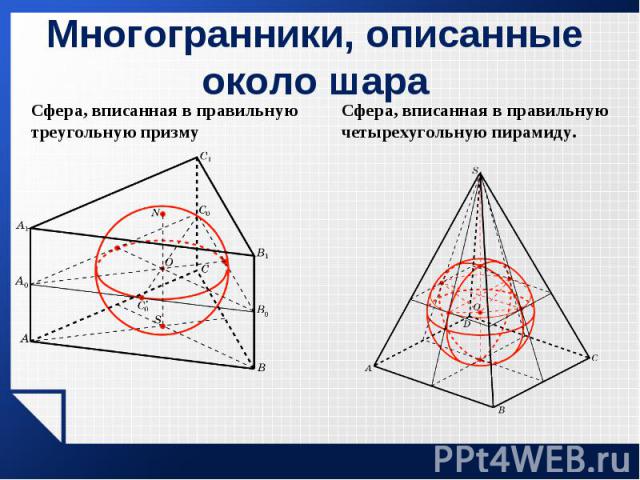
Теорема. Теорема. Шар можно вписать в прямую призму в том и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.

Каким свойством должна обладать прямая призма, чтобы в нее можно было вписать сферу? Каким свойством должна обладать прямая призма, чтобы в нее можно было вписать сферу? В основании прямой призмы лежит ромб. Можно ли в эту призму вписать сферу? При каком условии в прямую треугольную призму можно вписать сферу?

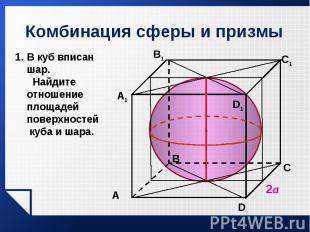
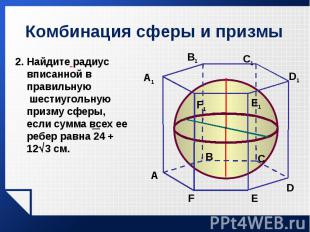
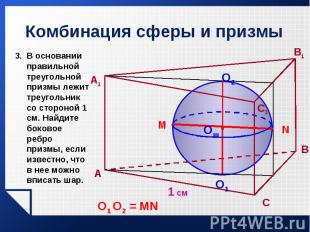
Из учебника Л.С.Атанасяна № 632. Из учебника Л.С.Атанасяна № 632.

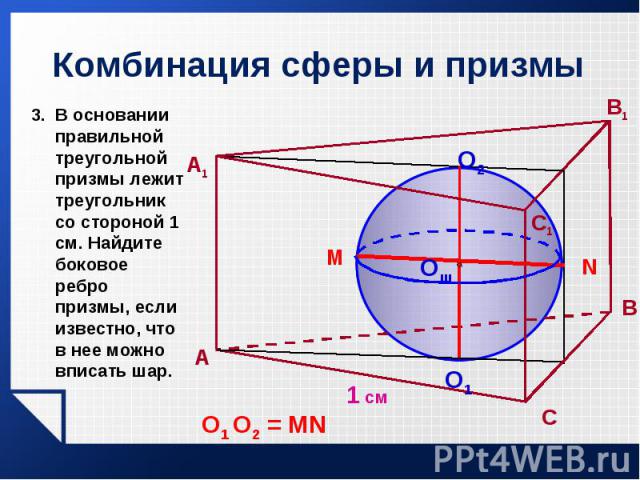
Теорема. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар. Теорема. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.

Приведите пример пирамиды, в которую нельзя вписать сферу? Приведите пример пирамиды, в которую нельзя вписать сферу? При каком условии в правильную четырехугольную усеченную пирамиду можно вписать сферу?

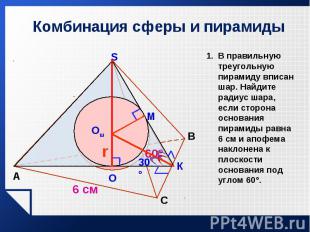
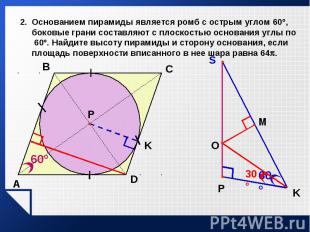
Из учебника Л.С.Атанасяна № 635, №638 (б), №640, №641. Из учебника Л.С.Атанасяна № 635, №638 (б), №640, №641.

Шар, описанный около правильной усеченной пирамиды. Шар, описанный около правильной усеченной пирамиды. Теорема . Около любой правильной усеченной пирамиды можно описать шар. (Это условие является достаточным, но не является необходимым) Шар, вписанный в правильную усеченную пирамиду. Теорема . В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований.

При каком условии в правильную четырехугольную усеченную пирамиду можно вписать сферу? При каком условии в правильную четырехугольную усеченную пирамиду можно вписать сферу? В треугольную усеченную пирамиду вписана сфера. Какая точка пирамиды является центром сферы?

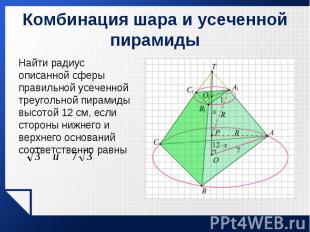
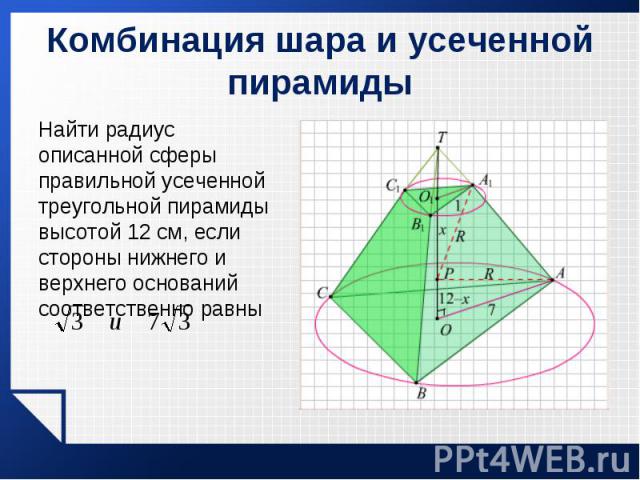
Найти радиус описанной сферы правильной усеченной треугольной пирамиды высотой 12 см, если стороны нижнего и верхнего оснований соответственно равны Найти радиус описанной сферы правильной усеченной треугольной пирамиды высотой 12 см, если стороны нижнего и верхнего оснований соответственно равны

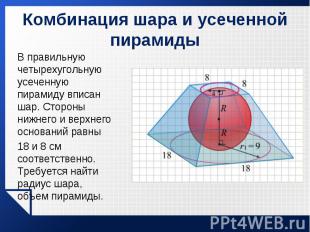
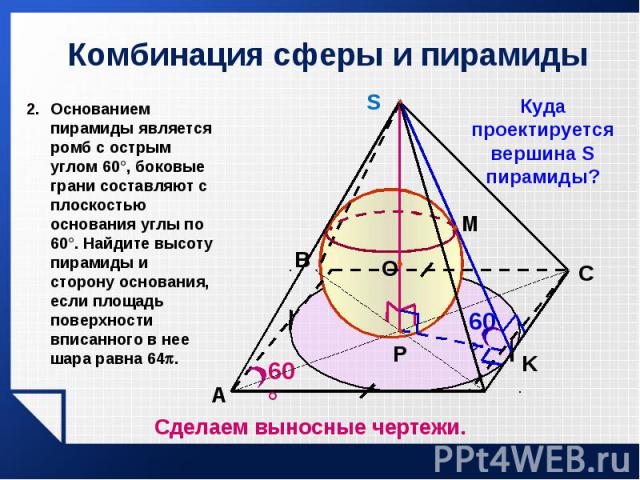
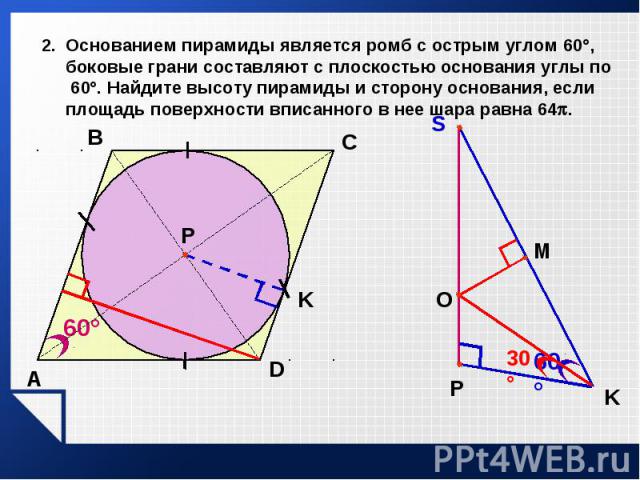
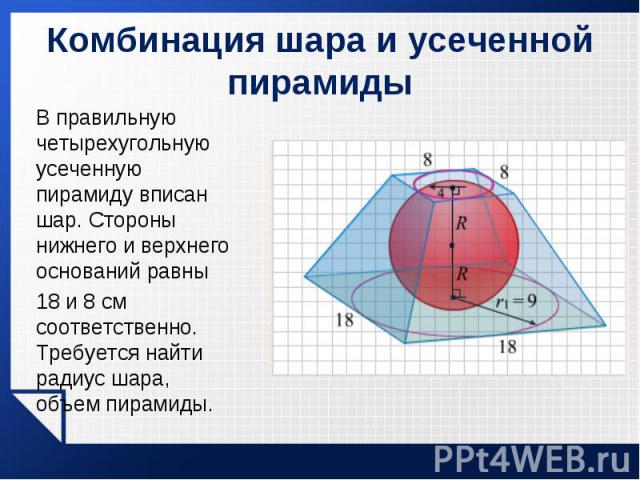
В правильную четырехугольную усеченную пирамиду вписан шар. Стороны нижнего и верхнего оснований равны В правильную четырехугольную усеченную пирамиду вписан шар. Стороны нижнего и верхнего оснований равны 18 и 8 см соответственно. Требуется найти радиус шара, объем пирамиды.

Из учебника Л.С.Атанасяна № 636. Из учебника Л.С.Атанасяна № 636.

Теорема. Около цилиндра, усеченного конуса (прямых круговых), конуса можно описать шар. Теорема. Около цилиндра, усеченного конуса (прямых круговых), конуса можно описать шар. Теорема. В цилиндр (прямой круговой) можно вписать шар в том и только в том случае, если цилиндр равносторонний.

Можно ли описать сферу около цилиндра (прямого кругового)? Можно ли описать сферу около цилиндра (прямого кругового)? Можно ли описать сферу около конуса, усеченного конуса (прямых круговых)? Во всякий ли цилиндр можно вписать сферу? Какими свойствами должен обладать цилиндр, чтобы в него можно было вписать сферу Во всякий ли конус можно вписать сферу? Как определить положение центра сферы, вписанной в конус? ?

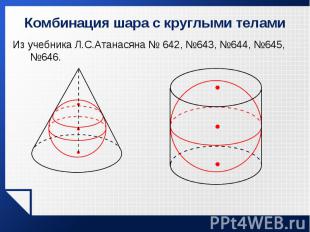
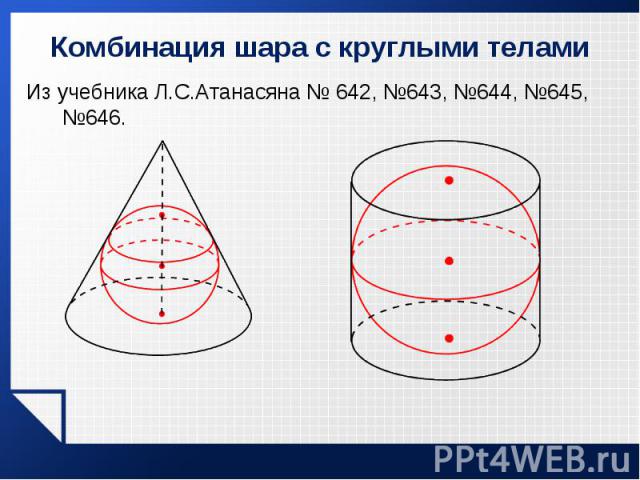
Из учебника Л.С.Атанасяна № 642, №643, №644, №645, №646. Из учебника Л.С.Атанасяна № 642, №643, №644, №645, №646.

На изучение темы «Разные задачи на многогранники, цилиндр, конус и шар» по планированию отводятся три урока. За такое короткое время детально изучить тему, научить учащихся решать задачи очень трудно. Поэтому, проект создан с целью помочь учителю в достижении поставленных целей. На изучение темы «Разные задачи на многогранники, цилиндр, конус и шар» по планированию отводятся три урока. За такое короткое время детально изучить тему, научить учащихся решать задачи очень трудно. Поэтому, проект создан с целью помочь учителю в достижении поставленных целей. Данный материал содержит теоретические сведения по данной теме, а также набор устных вопросов и задач, учитель может использовать в зависимости от степени подготовленности и уровня развития учащихся конкретного класса. Проект был опробован на уроках геометрии в 11 «А» классе 2009 – 2010 уч. года. Это общеобразовательный класс со средней успеваемостью.

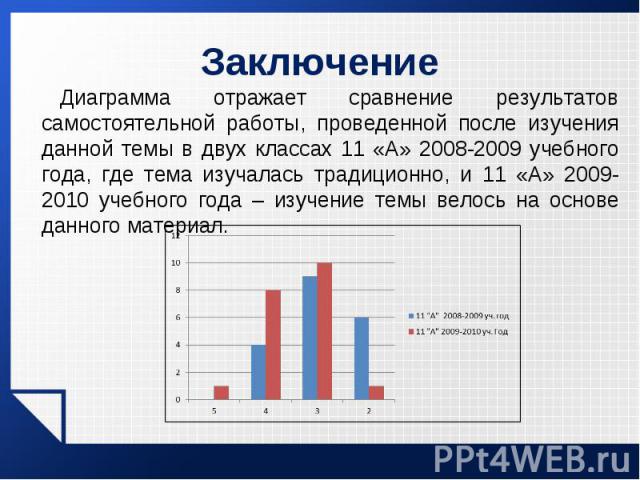
Диаграмма отражает сравнение результатов самостоятельной работы, проведенной после изучения данной темы в двух классах 11 «А» 2008-2009 учебного года, где тема изучалась традиционно, и 11 «А» 2009-2010 учебного года – изучение темы велось на основе данного материал. Диаграмма отражает сравнение результатов самостоятельной работы, проведенной после изучения данной темы в двух классах 11 «А» 2008-2009 учебного года, где тема изучалась традиционно, и 11 «А» 2009-2010 учебного года – изучение темы велось на основе данного материал.

Использование компьютера на уроках – это не дань моде, не способ переложить на плечи компьютера многогранный творческий труд учителя, а лишь одно из средств, позволяющих активизировать познавательную деятельность, увеличить эффективность урока. Использование компьютера на уроках – это не дань моде, не способ переложить на плечи компьютера многогранный творческий труд учителя, а лишь одно из средств, позволяющих активизировать познавательную деятельность, увеличить эффективность урока. «Детская природа ясно требует наглядности. Учите ребенка каким-нибудь пяти неизвестным ему словам, и он будет долго и напрасно мучиться над ними; но свяжите с картинками двадцать таких слов - и ребенок усвоит их на лету. Вы объясняете ребенку очень простую мысль, и он вас не понимает; вы объясняете тому же ребенку сложную картину, и он вас понимает быстро... Если вы входите в класс, от которого трудно добиться слова.,,, начните показывать картинки, и класс заговорит, а главное, заговорит свободно…». К.Д. Ушинский

http://saripkro.r2.ru/for_teacher/konkurs/matem/grish/index.htm http://saripkro.r2.ru/for_teacher/konkurs/matem/grish/index.htm http://eor.edu.ru/card/2569/zadachi-na-kombinacii-mnogogrannikov-i-tel-vrasheniya-i1.html http://festival.1september.ru/articles/502677/ http://festival.1september.ru/articles/211460/ http://www.it-n.ru/