Презентация на тему: Декартова система

Урок геометрии в 10-м классе по теме: "Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка"

Цель урока: Рассмотреть понятие системы координат и координаты точки в пространстве; вывести формулу расстояния в координатах; вывести формулу координат середины отрезка.

РЕНЕ ДЕКАРТ— французский ученый (1596— 1650) Декарт был крупнейшим философом и математиком своего времени. В основе его философии лежал материализм. Самым известным трудом Декарта является его “Геометрия”. Декарт ввел систему координат, которой пользуются все и в настоящее время. Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию. Эти открытия Декарта дали огромный толчок развитию как геометрии, так и другим разделам математики, оптики. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа - отрезками и выполнять арифметические действия над отрезками и другими геометрическими величинами, а также различными функциями. Это был совершенно новый метод, отличавшийся красотой, изяществом и простотой.

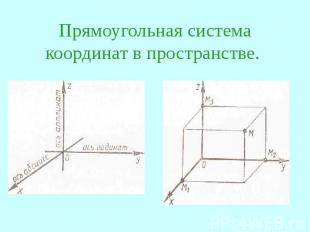
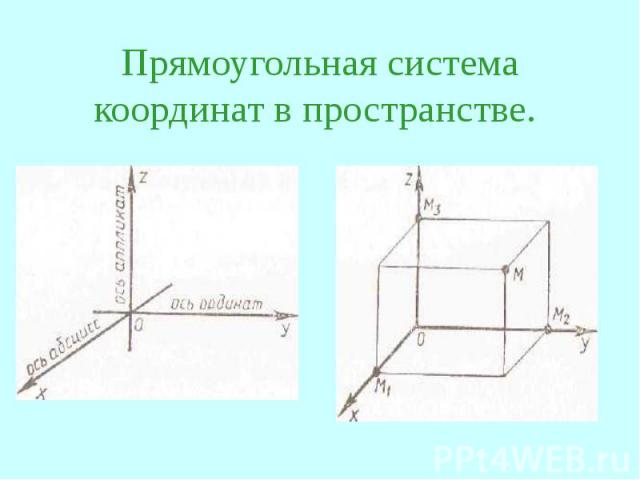
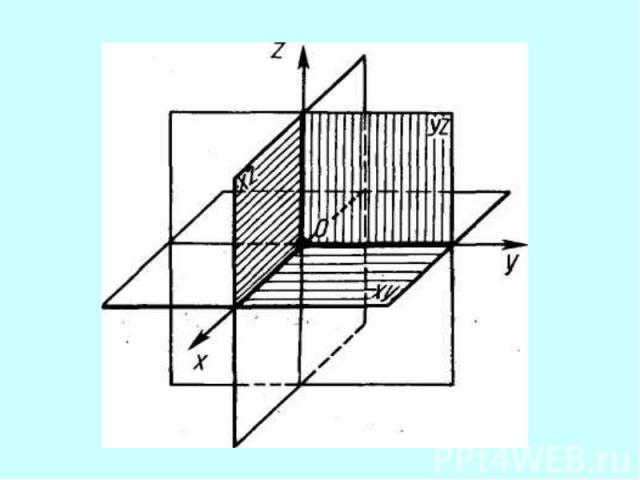
Прямоугольная система координат в пространстве.

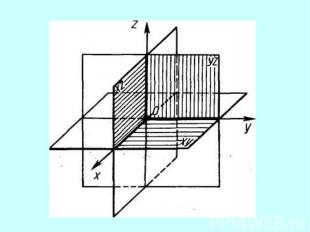
Координаты точки в пространстве. А (9; 5; 10); В (4; -3; 6); С (9; 0; 0); D (4; 0; 5); E (0; 8; 0); F (0; 0; -3)

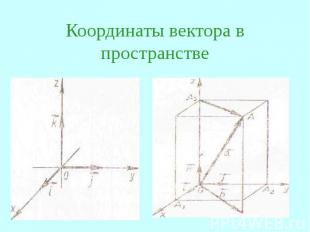
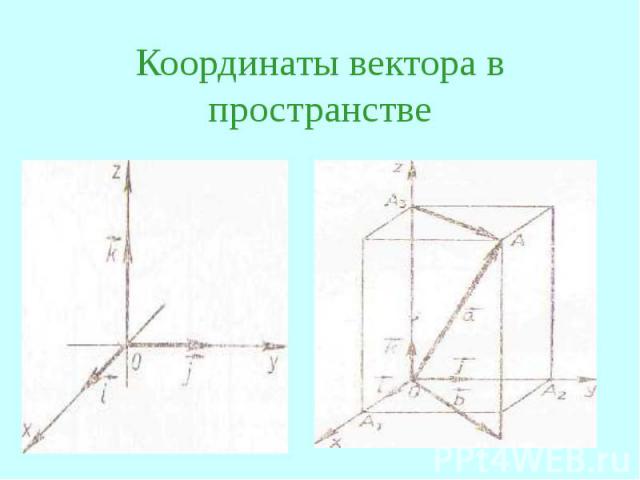
Координаты вектора в пространстве

Связь между координатами векторов и координатами точек. Координаты любой точки равны соответствующим координатам ее радиус – вектора.

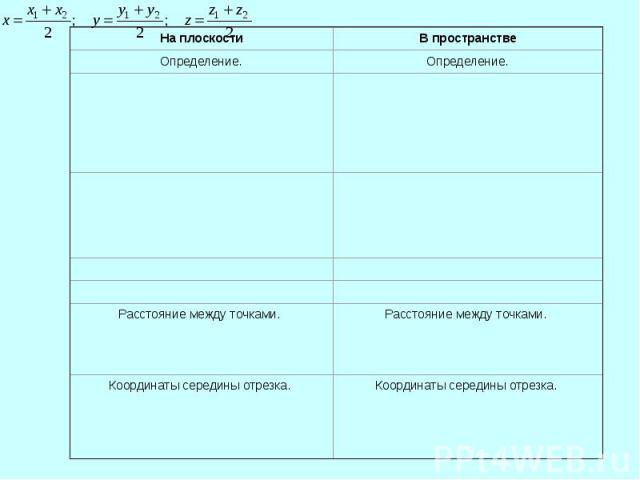
Вопросы для заполнения первой части таблицы. 1. Сформулируйте определение декартовой системы координат? 2. Попробуйте сформулировать определение декартовой системы координат в пространстве? 3. Назовите оси координат на плоскости? Назовите оси координат в пространстве? Название, какой оси мы не изучали? (Знакомство с новым словом “аппликата”) 4. Какие плоскости рассматриваются в планиметрии (в пространстве)? 5. Назовите координату начала координат на плоскости (в пространстве)? 6. Какие еще компоненты должна иметь система координат на плоскости и в пространстве? 7. Как задается координата точки на плоскости и в пространстве?

Вопросы для заполнения второй части таблицы. 1. Запишите формулу расстояния между точками на плоскости. 2. Как бы вы записали формулу расстояния между точками в пространстве?

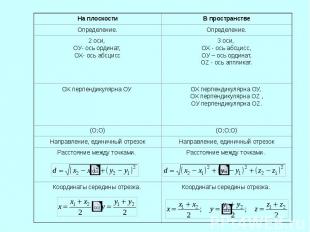
Итог урока. Как вводится, декартова система координат? Из чего она состоит? Как определяются координаты точки в пространстве? Чему равна координата начала координат? Чему равно расстояние от начала координат до заданной точки? Назовите формулу координат середины отрезка и расстояния между точками в пространстве?