Презентация на тему: Геометрия правильные многоугольники

Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны

Каково бы ни было число n, больше двух, существует правильный n-угольник. Каково бы ни было число n, больше двух, существует правильный n-угольник. Возьмем какую-нибудь окружность с центром в точке О и разделим её на n равных дуг. Для этого проведем радиусы ОА1, ОА2,…, ОАn этой окружности так, чтобы угол А1ОА2= угол А2ОА3 =…= угол Аn-1ОАn= угол АnОА1= 360°/n (на рисунке n=8). Если теперь провести отрезки А1А2, А2А3,…, Аn-1Аn, АnА1, то получим n- угольник А1А2…Аn. Треугольники А1ОА2, А2ОА3,…, АnОА1 равны друг другу (ДОКАЖИТЕ!), поэтому А1А2= А2А3=…= Аn-1Аn= АnА1. Отсюда следует, что А1А2…Аn- правильный n- угольник.

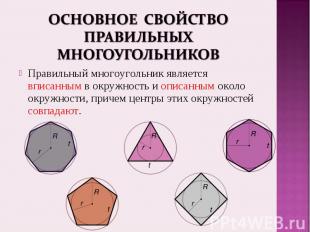
Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают. Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают.

В каждом правильном многоугольнике есть точка, равноудаленная от всех его вершин и всех его сторон- центр. В каждом правильном многоугольнике есть точка, равноудаленная от всех его вершин и всех его сторон- центр. ДОКАЖИТЕ!

Пусть АО, ВО, СО – биссектрисы углов правильного многоугольника Пусть АО, ВО, СО – биссектрисы углов правильного многоугольника Рассмотрите треугольники АОВ, ВОС,… ДОКАЖИТЕ, что АО= ВО = СО=… СДЕЛАЙТЕ ВЫВОД.

Пусть АВС…-правильный многоугольник, О- центр описанной окружности. Пусть АВС…-правильный многоугольник, О- центр описанной окружности. Высоты треугольников АОВ, ВОС,… равны между собой. ДОКАЖИТЕ! Сделайте вывод.

Классическая геометрия признает только построения при помощи циркуля и линейки Классическая геометрия признает только построения при помощи циркуля и линейки

Простейшее построение правильного четырехугольника Простейшее построение правильного четырехугольника Построение правильного восьмиугольника

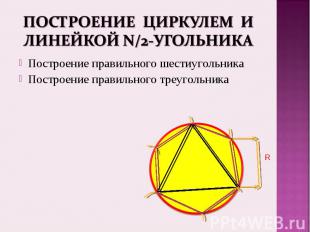
Построение правильного шестиугольника Построение правильного шестиугольника Построение правильного треугольника

Правильные многоугольники – воплощение красоты и изящества. Они заслуживают пристального внимания и изучения. Правильные многоугольники – воплощение красоты и изящества. Они заслуживают пристального внимания и изучения.

1)Учебник «Геометрия 8-9», автор Александров А.Д. и др.,Москва «Просвещение»,1991год. 1)Учебник «Геометрия 8-9», автор Александров А.Д. и др.,Москва «Просвещение»,1991год. Учебник "Геометрия 7-9", автор Атанасян Л.С. и др., Москва "Просвещение", 2003 год. 2) Геометрия . Дополнительные главы к школьному учебнику 9 класса, авторы Атанасян Л.С. и др., Москва,"Просвещение", 1997 год. 3) Математика. Энциклопедия для детей, Москва, "Аванта +", 1998 год. ru.wikipedia.org/wiki/ schools.techno.ru/sch758/geometr/prav.htm   www.mccme.ru/free-books/prasolov/planim/gl6s6.htm   www.exponenta.ru/educat/class/test/showitem/?item=120   www.9151394.ru/projects/math/livegeom/03_2001/4/4.htm