Презентация на тему: Геометрия пирамида

Изучить дополнительные источники и собрать исторический и занимательный материал о пирамиде. Изучить дополнительные источники и собрать исторический и занимательный материал о пирамиде. Рассмотреть теоретический материал по пирамиде, выходящий за рамки школьной программы. Научиться применять теоремы при решении задач на пирамиду. Изготовить развертки и модели разных пирамид.

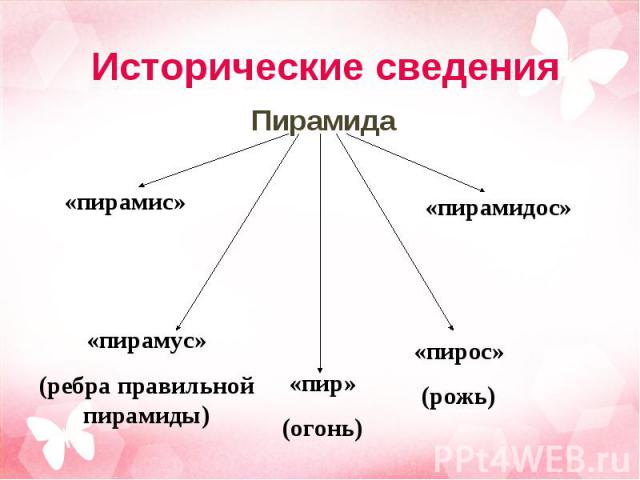
Пирамида Пирамида

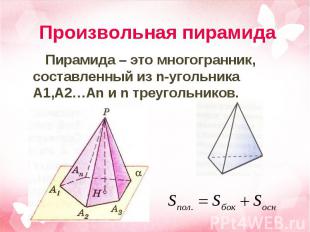
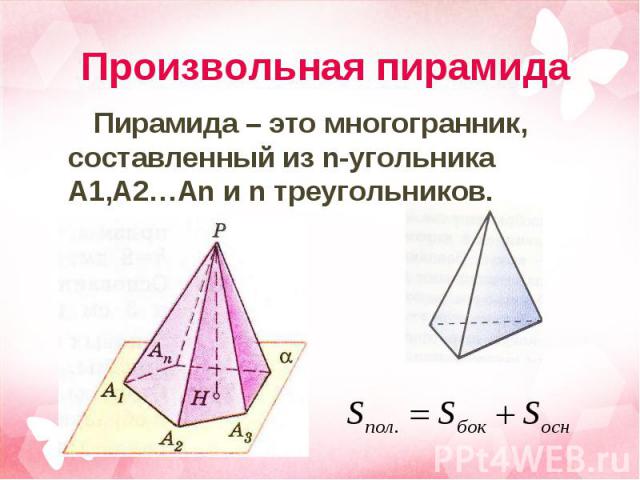
Пирамида – это многогранник, составленный из n-угольника A1,A2…An и n треугольников. Пирамида – это многогранник, составленный из n-угольника A1,A2…An и n треугольников.

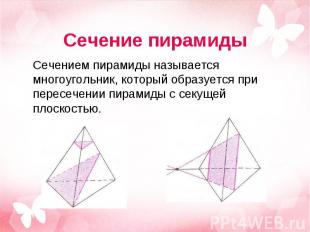
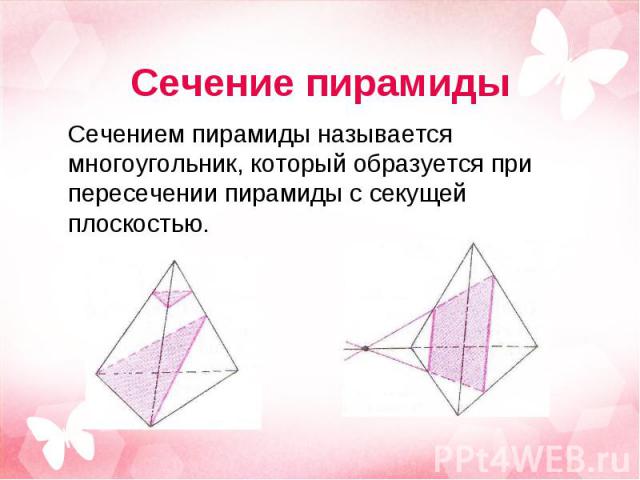
Если пирамида пересечена плоскостью, параллельной основанию, то: Если пирамида пересечена плоскостью, параллельной основанию, то: Сечение – многоугольник, подобный основанию; Площадь сечения и основания относятся как квадраты их расстояний от вершины.

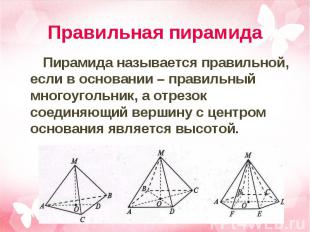
Пирамида называется правильной, если в основании – правильный многоугольник, а отрезок соединяющий вершину с центром основания является высотой. Пирамида называется правильной, если в основании – правильный многоугольник, а отрезок соединяющий вершину с центром основания является высотой.

У правильной пирамиды: У правильной пирамиды: боковые ребра равны; боковые грани являются равными равнобедренными треугольниками; апофемы равны; площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Дано: PA1A2…An – правильная пирамида Дано: PA1A2…An – правильная пирамида а – сторона основания; h – апофема Доказать: 1. PA1=PA2=…=PАn 2.PA1A2=PA2A3=…=PAnA1 – равнобедренные треугольники 3.PE1=PE2=…=PEn 4. Sбок. =Pосн.h

Тетраэдр, гранями которого являются правильные треугольники, называется правильным. Тетраэдр, гранями которого являются правильные треугольники, называется правильным.

Теорема: Объем правильной четырехугольной пирамиды равен одной трети произведения площади основания на высоту. Теорема: Объем правильной четырехугольной пирамиды равен одной трети произведения площади основания на высоту.

Теорема: Объем пирамиды равен одной третьи произведения площади основания на высоту Теорема: Объем пирамиды равен одной третьи произведения площади основания на высоту

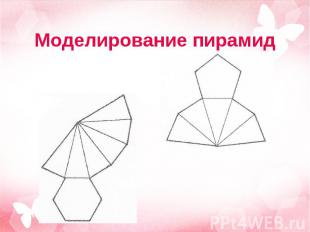
Решение: Решение: Объем пирамиды проще вычислить, если за основание принять равнобедренный прямоугольный треугольник с катетами а/2. Высотой пирамиды будет боковое ребро, равное а. Объем составит а /24 куб.ед.

Задача: Найти площадь развертки правильного тетраэдра с ребром 10 см. Задача: Найти площадь развертки правильного тетраэдра с ребром 10 см. Решение:

Задача: Найти площадь развертки усеченного тетраэдра с ребром 3,5 см Задача: Найти площадь развертки усеченного тетраэдра с ребром 3,5 см Решение:

Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые ребра пирамиды, если её высота проходит через точку пересечения диагоналей основания и равна 7 см. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые ребра пирамиды, если её высота проходит через точку пересечения диагоналей основания и равна 7 см.

Найдите объем пирамиды с высотой h, если h = 2 м, а основанием является квадрат со стороной 3 м Найдите объем пирамиды с высотой h, если h = 2 м, а основанием является квадрат со стороной 3 м Решение: Так как V= S осн. h, а в основании лежит квадрат, то V= 3 2= 6 м

О пирамидах О пирамидах В Древнем Египте жил египтянин,  Был фараон он, а может, крестьянин.  Как-то собрал он свои неликвиды,  Взял и построил из них пирамиды.  Как бы то ни было, но отчего-то Очень неплохо он с них заработал.  Тот египтянин теперь знаменит:  Гений финансовых он пирамид. 

На изучение темы «Пирамида» в 9 классе отведен один урок. На уроке я получила начальные сведения о пирамиде. В данной работе я попыталась расширить свои знания. Мною был собран исторический материал о пирамиде и её объеме и занимательный материал: загадки, ребусы, кроссворды. На изучение темы «Пирамида» в 9 классе отведен один урок. На уроке я получила начальные сведения о пирамиде. В данной работе я попыталась расширить свои знания. Мною был собран исторический материал о пирамиде и её объеме и занимательный материал: загадки, ребусы, кроссворды.

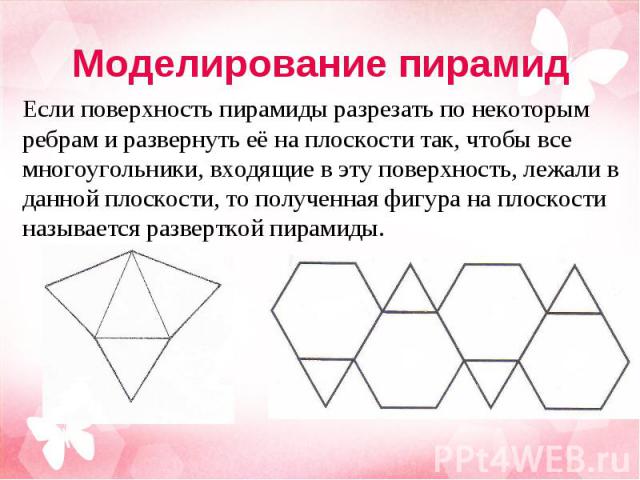
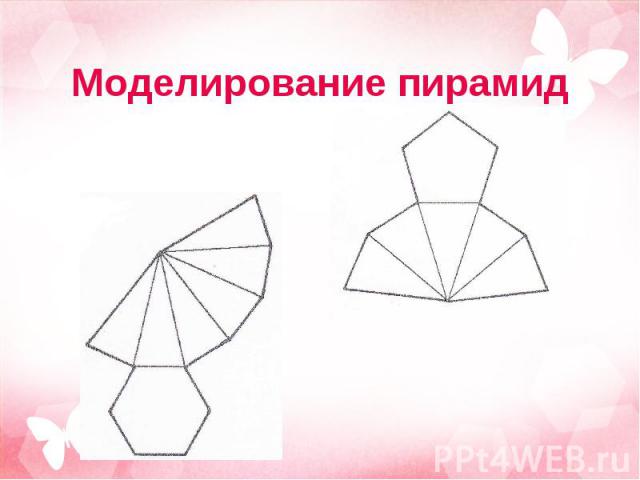
Так же я рассматривала теоретические вопросы, выходящие за рамки школьного курса геометрии 9 класса. Я изготовила развертки и модели различных пирамид, что помогает развитию пространственного воображения. При решении задач по теме «Пирамида» я повторила и обобщила знания по планиметрии. Материал, собранный в данной работе, поможет мне в дальнейшем изучении стереометрии в 10-11 классах. Так же я рассматривала теоретические вопросы, выходящие за рамки школьного курса геометрии 9 класса. Я изготовила развертки и модели различных пирамид, что помогает развитию пространственного воображения. При решении задач по теме «Пирамида» я повторила и обобщила знания по планиметрии. Материал, собранный в данной работе, поможет мне в дальнейшем изучении стереометрии в 10-11 классах.

Геометрия, 7-9:Учебник для общеобразовательного учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 14-е изд. – М: Просвещение 2004-384с. Геометрия, 7-9:Учебник для общеобразовательного учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 14-е изд. – М: Просвещение 2004-384с. Геометрия, 10-11: Учебник для общеобразовательного учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 13-е изд. – М: Просвещение 2004-206с. Зив Б.Г. Задачи к урокам геометрии 7-11 класс. – С. – Петербург, 1998 НПО «Мир и семья – 95»- 624с. Глейзер Г.И. История математики в школе: IX – X класс Пособие для учителей. – М.: Просвещение, 1983 – 351с.

Глейзер Г.И. История математики в школе: VII – VIII класс Пособие для учителей. – М.: Просвещение, 1982 – 240с. Глейзер Г.И. История математики в школе: VII – VIII класс Пособие для учителей. – М.: Просвещение, 1982 – 240с. Игнатьев Е.И. В царстве смекалки / Под редакцией М.К. Потанова – 4-е изд. – М.: Наука 1984, 192с. Энциклопедический словарь юного математика, - М.: Педагогика, 1985 Смирнова И.М. В мире многогранников – М.: Просвещение, 1995 Веннинджер М. Модели Многогранников – М.Мир, 1974 Штейнгауз Г. Математический калейдоскоп Штейнгауз Г. Сто задач. – М: Наука, 1982