Презентация на тему: Геометрия Лобачевского

ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО ПРЕЗЕНТАЦИЯ УРОКА – КОНФЕРЕНЦИИ Учитель: Иманова Алена Викторовна Школа: МБОУ « Средняя общеобразовательная школа № 21» г. Старый Оскол Белгородской области

Цель урока Познакомить учащихся с неевклидовой геометрией , ее создателями, некоторыми теоремами геометрии Лобачевского. Расширение представлений учащихся о мире: влияние создания неевклидовой геометрии на изучение геометрии Вселенной

…Чем Коперник был для Птолемея, тем был Лобачевский для Евклида… В. Клиффорд Геометрия Лобачевского - геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского

Создатели неевклидовойгеометрии Карл Фридрих Гаусс 1777-1855 ГАУСС НЕ ОПУБЛИКОВАЛ НИ ОДНОЙ РАБОТЫ ПО НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ, НО В ЕГО ДНЕВНИКАХ НАЙДЕНЫ МАТЕРИАЛЫ, КОТОРЫЕ ОБНАРУЖИВАЮТ, ЧТО ОН ПРИШЕЛ К МЫСЛИ О ВОЗМОЖНОСТИ ПОСТРОЕНИЯ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ .

Создатели неевклидовойгеометрии Николай Иванович Лобачевский 1792 - 1856 НАИБОЛЕЕ ПОЛНО РАЗРАБОТАЛ НЕЕВКЛИДОВУ ГЕОМЕТРИЮ. ЗАСЛУГОЙ ЛОБАЧЕВСКОГО , КАК УЧЕНОГО , ЯВЛЯЕТСЯ ТО, ЧТО ОН ВПЕРВЫЕ ПРОБИЛ БРЕШЬ В ВОСПРИЯТИИ ГЕОМЕТРИИ КАК ЕДИНСТВЕННО МЫСЛИМОЙ ЛОГИЧЕСКОЙ СИСТЕМЫ.

Создатели неевклидовойгеометрии Янош Больяй 1802 – 1860 УЖЕ К 1825 ГОДУ ПРИШЕЛ К ОСНОВНЫМ ПОЛОЖЕНИЯМ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ. ОПУБЛИКОВАЛ СВОИ ИССЛЕДОВАНИЯ В 1832 ГОДУ В ПРИЛОЖЕНИИ К ПЕРВОМУ ТОМУ СОЧИНЕНИЙ СВОЕГО ОТЦА – ПРОФЕССОРА МАТЕМАТИКИ.

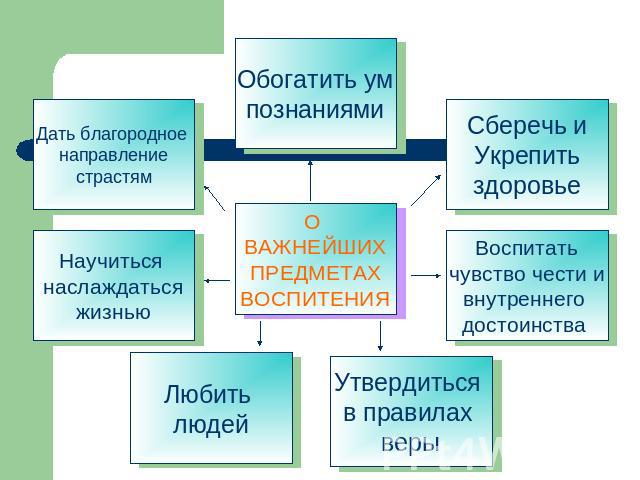
О ВАЖНЕЙШИХ ПРЕДМЕТАХ ВОСПИТЕНИЯ Обогатить ум познаниями Сберечь и Укрепить здоровье Воспитать чувство чести и внутреннего достоинства Утвердиться в правилах веры Любить людей Научиться наслаждаться жизнью Дать благородное направление страстям

Д е н ь р о ж д е н и я 23 (11) февраля 1826 года Н. И. Лобачевский впервые выступил с изложением своей геометрии перед учеными физико-математического факультета Казанского университета. Этот день считают днем рождения геометрии Лобачевского. Титульный лист первого издания «Воображаемой геометрии»

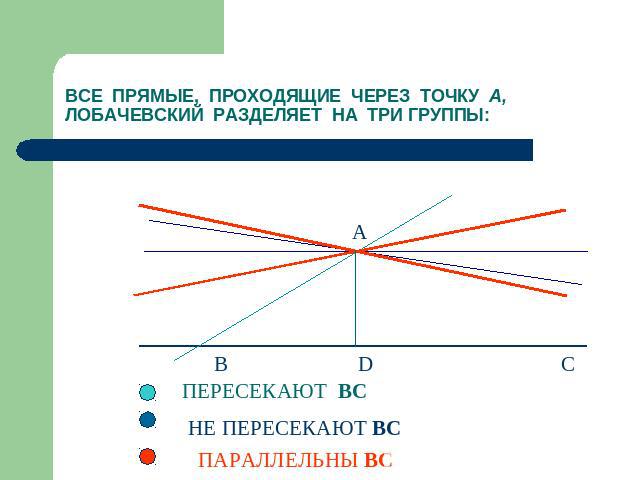
СКОЛЬКО ПРЯМЫХ, НЕ ПЕРЕСЕКАЮЩИХ ДАННУЮ ПРЯМУЮ И ПРОХОДЯЩИХ ЧЕРЕЗ ДАННУЮ ТОЧКУ, МОЖНО ПРОВЕСТИ В ДАННОЙ ПЛОСКОСТИ? АКСИОМА ПАРАЛЛЕЛЬНОСТИ ЕВКЛИДА: ЧЕРЕЗ ТОЧКУ ВНЕ ПРЯМОЙ НА ДАННОЙ ПЛОСКОСТИ МОЖНО ПРОВЕСТИ НЕ БОЛЕЕ ОДНОЙ ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ ДАННОЙ. ЛОБАЧЕВСКИЙ РАССМАТРИВАЕТ ДРУГУЮ ВОЗМОЖНОСТЬ: ПРИНЯТЬ, ЧТО ЧЕРЕЗ ТОЧКУ ВНЕ ПРЯМОЙ НА ДАННОЙ ПЛОСКОСТИ МОЖНО ПРОВЕСТИ БОЛЕЕ ОДНОЙ ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ ДАННОЙ.

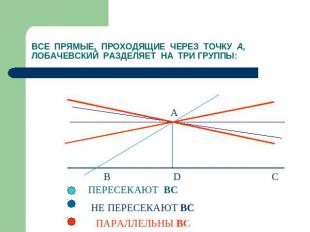
ВСЕ ПРЯМЫЕ, ПРОХОДЯЩИЕ ЧЕРЕЗ ТОЧКУ А, ЛОБАЧЕВСКИЙ РАЗДЕЛЯЕТ НА ТРИ ГРУППЫ: ПЕРЕСЕКАЮТ BC НЕ ПЕРЕСЕКАЮТ BC ПАРАЛЛЕЛЬНЫ ВС

НЕКОТОРЫЕ ФАКТЫ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО 1. Сумма углов треугольника меньше 180о ,меняется от треугольника к треугольнику и может приближаться к нулю. 2. Сумма углов всякого выпуклого четырехугольника меньше 360 о и поэтому не существует прямоугольников. 3. В геометрии Лобачевского не существуют подобные треугольники. 4. В геометрии Лобачевского два треугольника равны, если три угла одного треугольника равны трем углам другого. 5. Для любого заданного угла α можно найти такой перпендикулярный отрезок к данной прямой, что угол параллельности равен α.

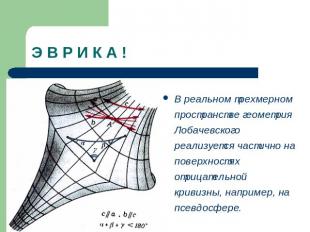
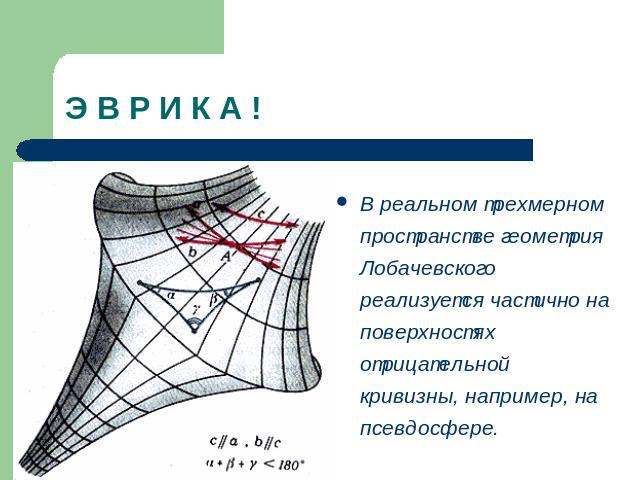
Э В Р И К А ! В реальном трехмерном пространстве геометрия Лобачевского реализуется частично на поверхностях отрицательной кривизны, например, на псевдосфере.

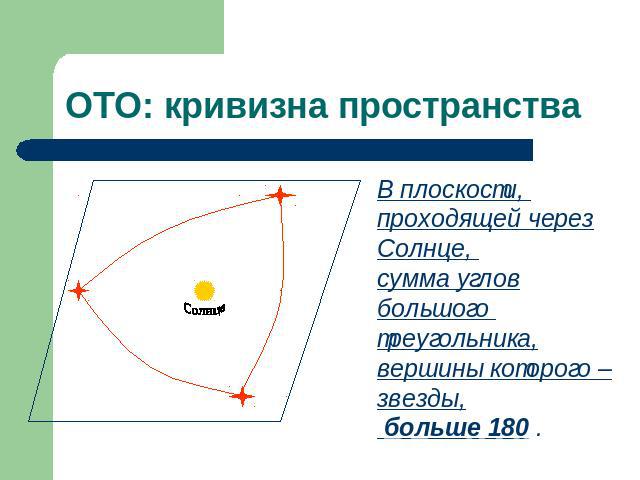
Геометрия и физическая картина мира Лобачевский, показав, что евклидова геометрия не единственна, поставил вопрос о геометрии пространства, в котором развивается Вселенная. Созданная Эйнштейном общая теория относительности установила связь между силой всемирного тяготения и свойствами пространства: пространство в котором мы живем искривлено. Вблизи тяжелых тел, например, вблизи Солнца, механика становится не ньютоновой, а геометрия пространства – неевклидовой.

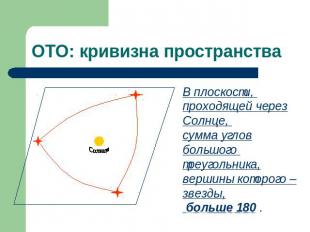
ОТО: кривизна пространства В плоскости, проходящей через Солнце, сумма углов большого треугольника, вершины которого – звезды, больше 180 .

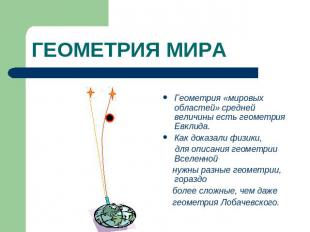
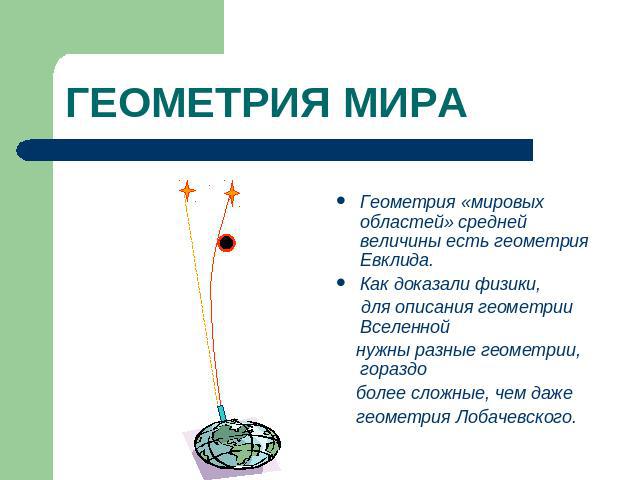
ГЕОМЕТРИЯ МИРА Геометрия «мировых областей» средней величины есть геометрия Евклида. Как доказали физики, для описания геометрии Вселенной нужны разные геометрии, гораздо более сложные, чем даже геометрия Лобачевского.

Александров П. С. Николай Иванович Лобачевский. «Квант». 1976. № 2. Александров П. С. Николай Иванович Лобачевский. «Квант». 1976. № 2. vivovoco.rsl.ru/VV/Q_PROJECT/HEAP/8... Александров П. С. Тупость и гений. «Квант». 1982. №№11, 12 Глейзер Г. И. История математики в школе IX-X классы. — М.: Просвещение, 1983. — С. 348-362. ru.wikipedia.org/wiki/Геометрия_Лобачевского. ru.wikipedia.org/wiki/Лобачевский,_... vivovoco.rsl.ru     GIF 310×310, 18 КБ