Презентация на тему: Геометрия Лобачевского


Сотни профессиональных геометров разных времён и народов, тысячи любителей математики в течение 20-х веков искали доказательство пятого постулата. Дальше всех в этих математических битвах зашли учёные XVIII века Саккери (Италия), Ламберт (Швейцария) и Лежандр (Франция) Сотни профессиональных геометров разных времён и народов, тысячи любителей математики в течение 20-х веков искали доказательство пятого постулата. Дальше всех в этих математических битвах зашли учёные XVIII века Саккери (Италия), Ламберт (Швейцария) и Лежандр (Франция)
Ближе всех к победе над пятым постулатом приблизился великий русский математик Николай Иванович Лобачевский (1792-1856) Ближе всех к победе над пятым постулатом приблизился великий русский математик Николай Иванович Лобачевский (1792-1856)



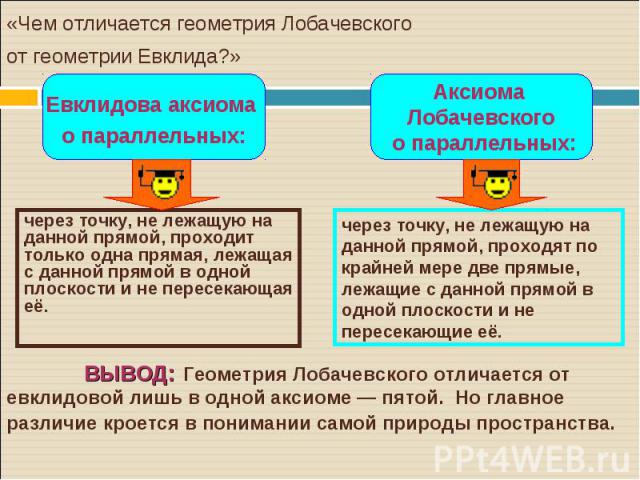
Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, о параллельных прямых. Оказалось то, что пятый постулат не зависит от предыдущих, а значит, его можно заменить на ему эквивалентный. Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, о параллельных прямых. Оказалось то, что пятый постулат не зависит от предыдущих, а значит, его можно заменить на ему эквивалентный. Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского.
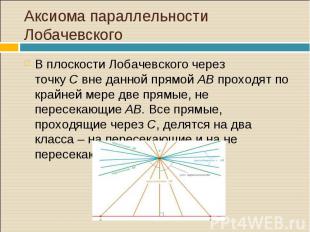
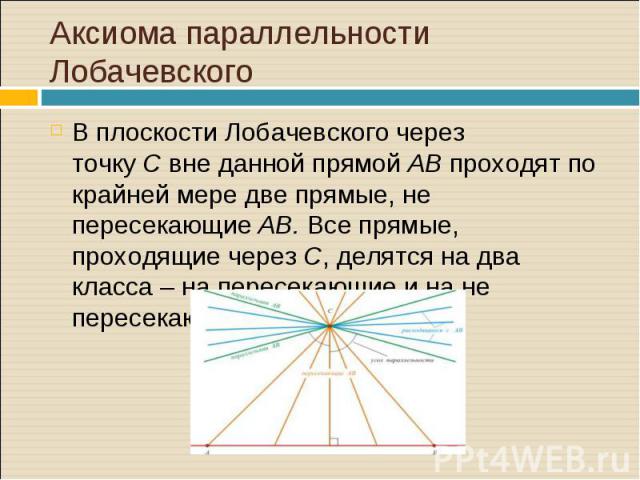
В плоскости Лобачевского через точку C вне данной прямой AB проходят по крайней мере две прямые, не пересекающие AB. Все прямые, проходящие через C, делятся на два класса – на пересекающие и на не пересекающие AB. В плоскости Лобачевского через точку C вне данной прямой AB проходят по крайней мере две прямые, не пересекающие AB. Все прямые, проходящие через C, делятся на два класса – на пересекающие и на не пересекающие AB.
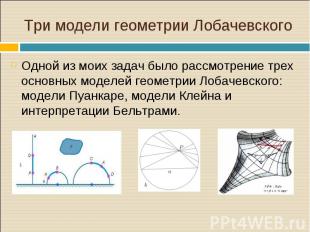
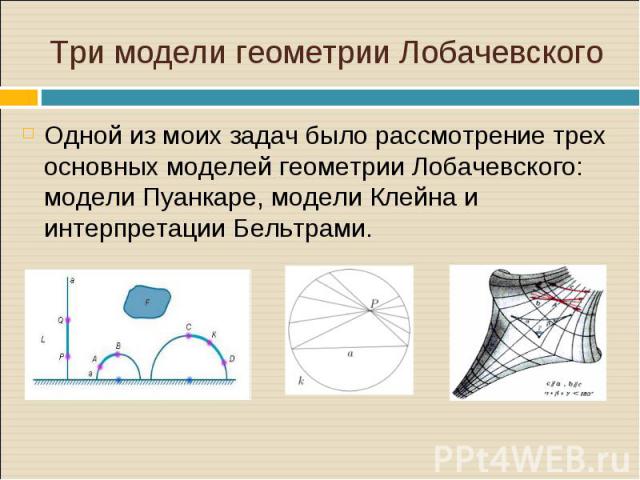
Одной из моих задач было рассмотрение трех основных моделей геометрии Лобачевского: модели Пуанкаре, модели Клейна и интерпретации Бельтрами. Одной из моих задач было рассмотрение трех основных моделей геометрии Лобачевского: модели Пуанкаре, модели Клейна и интерпретации Бельтрами.

Модель Пуанкаре (часто называется диск Пуанкаре) — модель пространства Лобачевского, предложенная Анри Пуанкаре в 1882 году в связи с задачами теории функций комплексного переменного. Существуют разновидности модели — в круге и на полуплоскости для планиметрии Лобачевского, а также в шаре и в полупространстве — для стереометрии Лобачевского, соответственно. Модель Пуанкаре (часто называется диск Пуанкаре) — модель пространства Лобачевского, предложенная Анри Пуанкаре в 1882 году в связи с задачами теории функций комплексного переменного. Существуют разновидности модели — в круге и на полуплоскости для планиметрии Лобачевского, а также в шаре и в полупространстве — для стереометрии Лобачевского, соответственно.

В модели Клейна за плоскость принимается внутренность какой-либо окружности, за точки - точки принадлежащие этому кругу, за прямые - хорды - конечно, с исключением концов, поскольку рассматривается только внутренность круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. В модели Клейна за плоскость принимается внутренность какой-либо окружности, за точки - точки принадлежащие этому кругу, за прямые - хорды - конечно, с исключением концов, поскольку рассматривается только внутренность круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями.
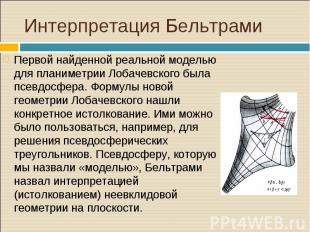
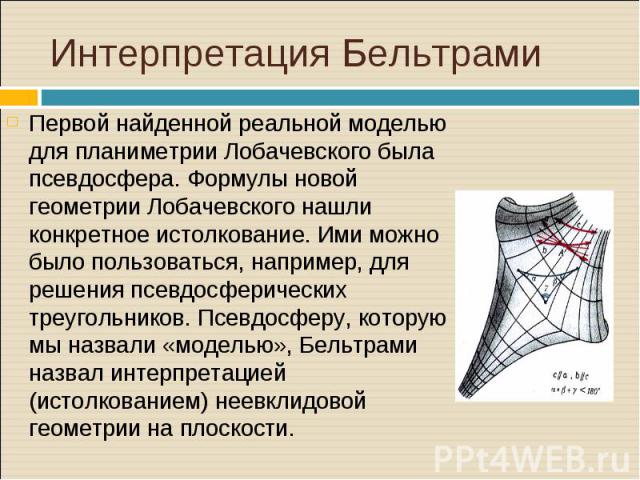
Первой найденной реальной моделью для планиметрии Лобачевского была псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости. Первой найденной реальной моделью для планиметрии Лобачевского была псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости.
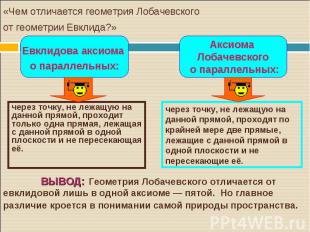
через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её.

Лобачевский всю жизнь занимался созданной им «воображаемой геометрией», но в этой воображаемой науке не было ничего фантастического. Она была и есть несомненная реальная истина. Лобачевский всю жизнь занимался созданной им «воображаемой геометрией», но в этой воображаемой науке не было ничего фантастического. Она была и есть несомненная реальная истина.

Геометрия Лобачевского находит свое применение в различных науках и областях деятельности человека, например: в географии, в теории чисел, в теории относительности, в астрономии, релятивистской физике и физике высоких энергий. Геометрия Лобачевского находит свое применение в различных науках и областях деятельности человека, например: в географии, в теории чисел, в теории относительности, в астрономии, релятивистской физике и физике высоких энергий.


Ознакомившись с содержанием геометрии Лобачевского, рассмотрев три ее основные модели и проанализировав аксиому параллельности Лобачевского, мы смогли ознакомится с основами данной геометрии и изучили ее основные модели, что помогло облегчить задачу понимания данной геометрии. Ознакомившись с содержанием геометрии Лобачевского, рассмотрев три ее основные модели и проанализировав аксиому параллельности Лобачевского, мы смогли ознакомится с основами данной геометрии и изучили ее основные модели, что помогло облегчить задачу понимания данной геометрии.