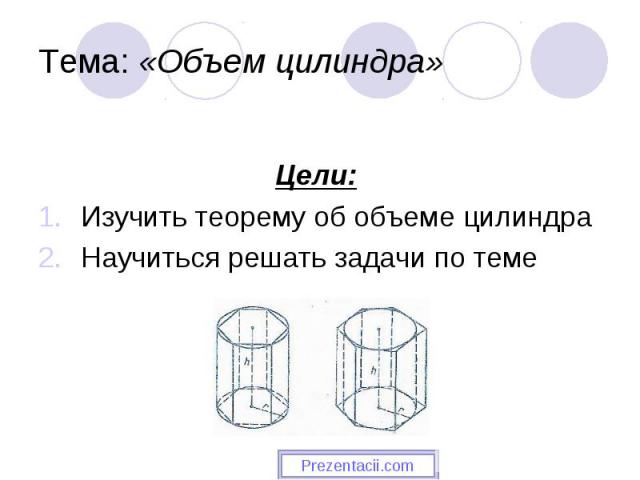
Презентация на тему: Объем цилиндра
Цели: Изучить теорему об объеме цилиндра Научиться решать задачи по теме

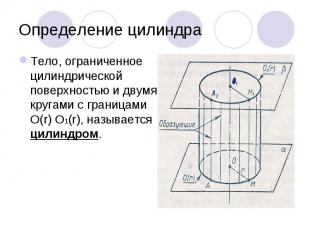
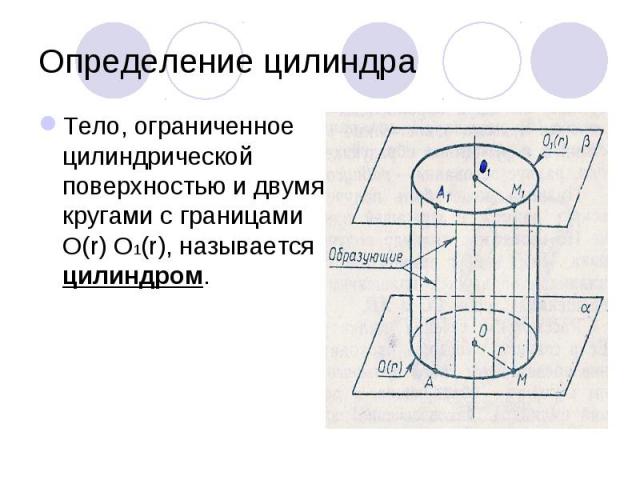
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами O(r) O1(r), называется цилиндром. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами O(r) O1(r), называется цилиндром.
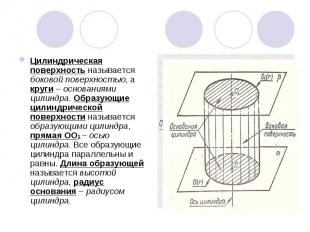
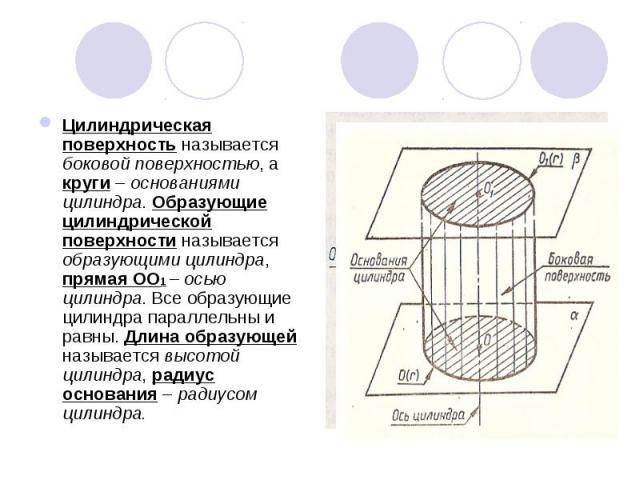
Цилиндрическая поверхность называется боковой поверхностью, а круги – основаниями цилиндра. Образующие цилиндрической поверхности называется образующими цилиндра, прямая ОО1 – осью цилиндра. Все образующие цилиндра параллельны и равны. Длина образующей называется высотой цилиндра, радиус основания – радиусом цилиндра. Цилиндрическая поверхность называется боковой поверхностью, а круги – основаниями цилиндра. Образующие цилиндрической поверхности называется образующими цилиндра, прямая ОО1 – осью цилиндра. Все образующие цилиндра параллельны и равны. Длина образующей называется высотой цилиндра, радиус основания – радиусом цилиндра.
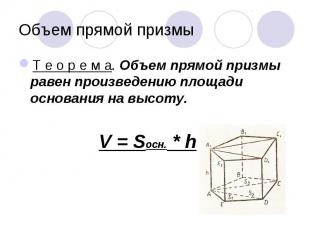
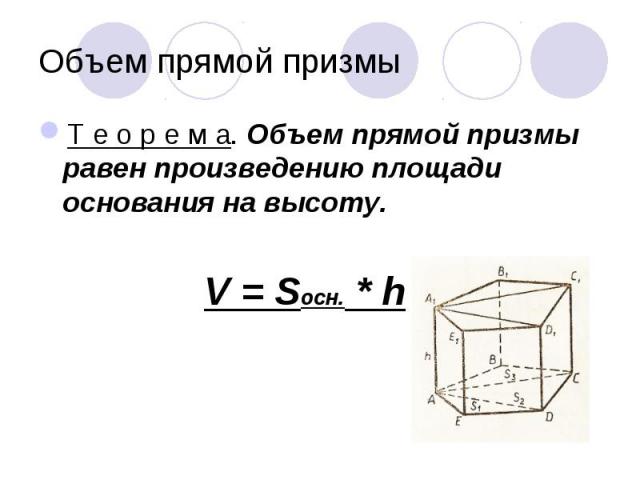
Т е о р е м а. Объем прямой призмы равен произведению площади основания на высоту. Т е о р е м а. Объем прямой призмы равен произведению площади основания на высоту. V = Sосн. * h
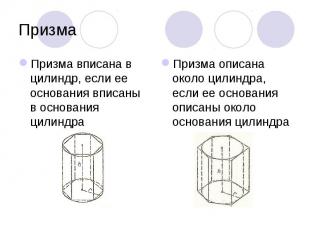
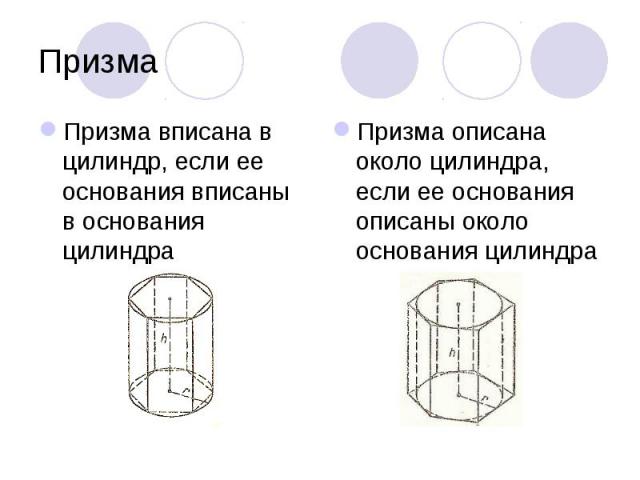
Призма вписана в цилиндр, если ее основания вписаны в основания цилиндра Призма вписана в цилиндр, если ее основания вписаны в основания цилиндра


Объем цилиндра равен произведению площади основания на высоту V = ПR^2 * H
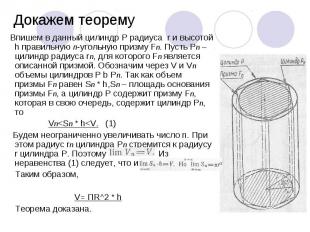
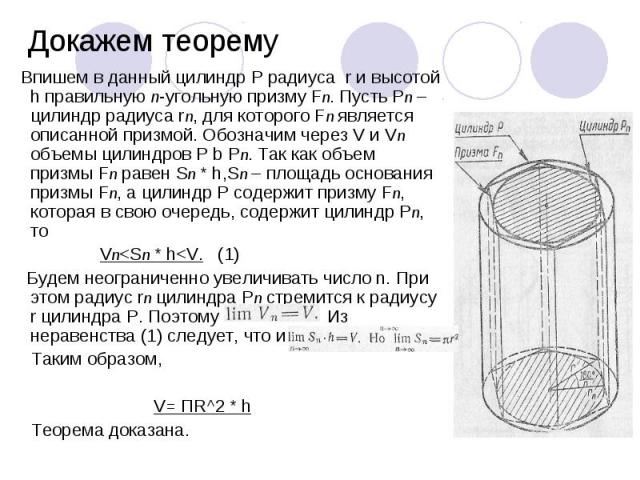
Впишем в данный цилиндр Р радиуса r и высотой h правильную n-угольную призму Fn. Пусть Рn – цилиндр радиуса rn, для которого Fn является описанной призмой. Обозначим через V и Vn объемы цилиндров Р b Pn. Так как объем призмы Fn равен Sn * h,Sn – площадь основания призмы Fn, а цилиндр Р содержит призму Fn, которая в свою очередь, содержит цилиндр Pn, то Впишем в данный цилиндр Р радиуса r и высотой h правильную n-угольную призму Fn. Пусть Рn – цилиндр радиуса rn, для которого Fn является описанной призмой. Обозначим через V и Vn объемы цилиндров Р b Pn. Так как объем призмы Fn равен Sn * h,Sn – площадь основания призмы Fn, а цилиндр Р содержит призму Fn, которая в свою очередь, содержит цилиндр Pn, то Vn<Sn * h<V. (1) Будем неограниченно увеличивать число n. При этом радиус rn цилиндра Pn стремится к радиусу r цилиндра P. Поэтому Из неравенства (1) следует, что и Таким образом, V= ПR^2 * h Теорема доказана.