Презентация на тему: Объем цилиндра

Объем цилиндра

Цилиндр: история Слово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток " …

Цилиндры из жизни

Цилиндры-башниВодовзводная башня (Москва) Собственный дом архитектора К.Мельникова (Москва) Замок Сфорца (Милан)

Объём цилиндраОснование цилиндра - круг

Объём цилиндра

Объём цилиндра

Объём цилиндра

Объём цилиндра Призма называется вписанной в цилиндр, если ее вершины лежат на окружностях, ограничивающих основания цилиндра Призма называется описанной около цилиндра, если ее основания - многоугольники, вписанные в основания цилиндра

Объём цилиндра

Объём цилиндраОбъём цилиндра равен произведению площади основания на высоту.

Вычисление объемов тел с помощью определенного интеграла

Если функция f(x) непрерывна на промежутке I числовой оси, содержащей точки х = а и х = b, то разность значений F (b) – F (a) (где F(x) - первообразная f(x) на I) называется определенным интегралом от функции f(x) от a до b.

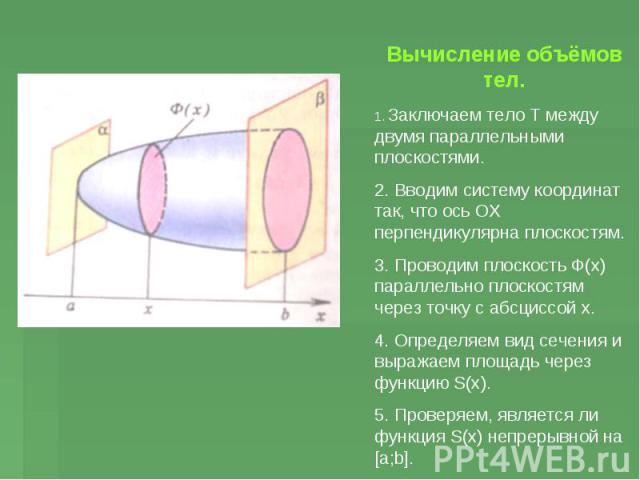
Вычисление объёмов тел. 1. Заключаем тело Т между двумя параллельными плоскостями. 2. Вводим систему координат так, что ось ОХ перпендикулярна плоскостям. 3. Проводим плоскость Ф(х) параллельно плоскостям через точку с абсциссой х. 4. Определяем вид сечения и выражаем площадь через функцию S(х). 5. Проверяем, является ли функция S(х) непрерывной на [a;b].

6. Разбиваем [a;b] на n - равных отрезков точками а = х0, х1, х2, …хn=b и проводим через хi плоскости перпендикулярно ОХ. 7. Плоскости разбивают тело Т на n- тел Т1, Т2, Т3,... Тn с основаниями Ф(хi) и высотой xi = (b - a)/n 8. V Vn= (S(x1) + S(x2) +…+ S (xn) ) xi = (S(x1) + S(x2) +… + S (xn))(b - a)/n. При n , Vn V, поэтому но 9.

Задача 1.Найти объём наклонной треугольной призмы с основанием S и высотой h. 1. Введём ось ОХ перпендикулярно основаниям призмы. 2. (АВС) OX=a, a=0, (A1B1C1) OX=b, b=h 3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х. А2В2С2-треугольник, равный основаниям. Площадь А2В2С2 равна S. 4. S(x) непрерывна на [0;h]

2. Докажем теперь теорему для произвольной призмы с высотой h и площадью основания S. Такую призму можно разбить на треугольные призмы с общей высотой h. Выразим объем каждой треуголь ной призмы по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т. е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен S * h. Теорема доказана.

АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА. 1. Ввести систему координат так, что ось ОХ перпендикулярна основанию геометрического тела. 2. Найти пределы интегрирования а и b. 3. Провести сечение плоскостью перпендикулярно оси ОХ через точку с абсциссой х. Определить вид сечения, задать формулой его площадь как функцию S(X). 4. Проверить непрерывность функции S(X) на [a;b]. 5.

Задание: Найти объёмы геометрических тел с помощью определённого интеграла.