Презентация на тему: Взаимное расположение прямых на плоскости

Взаимное расположение прямых на плоскости Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д.

Цели: Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса. Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в зависимости от k и b. Применить полученные знания при построении графиков кусочной функции.

Аксиома геометрии: Через любые две точки проходит прямая, и притом только одна.

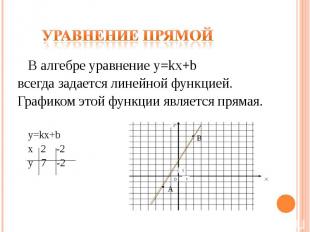
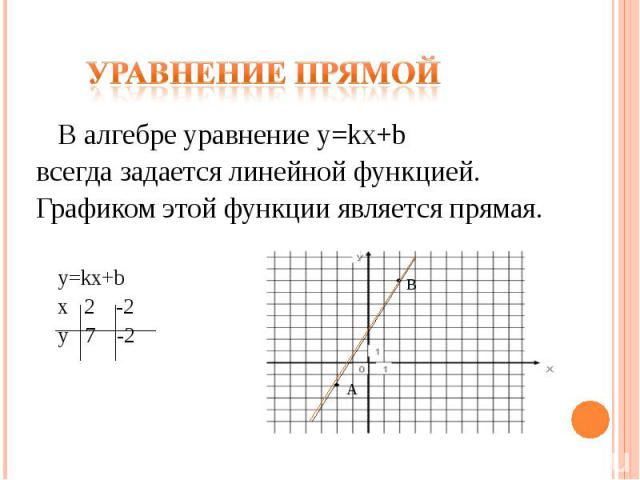
Уравнение прямой В алгебре уравнение y=kx+b всегда задается линейной функцией. Графиком этой функции является прямая. y=kx+b х 2 -2 y 7 -2

Параллельные и пересекающиеся прямые В геометрии на плоскости прямые а и b могут быть пересекающимися (рис.1) или параллельными (рис.2). Пересекающиеся прямые- это прямые, которые пересекаются в одной точке. Параллельные прямые- это прямые, которые не пересекаются .

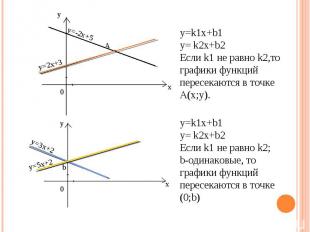
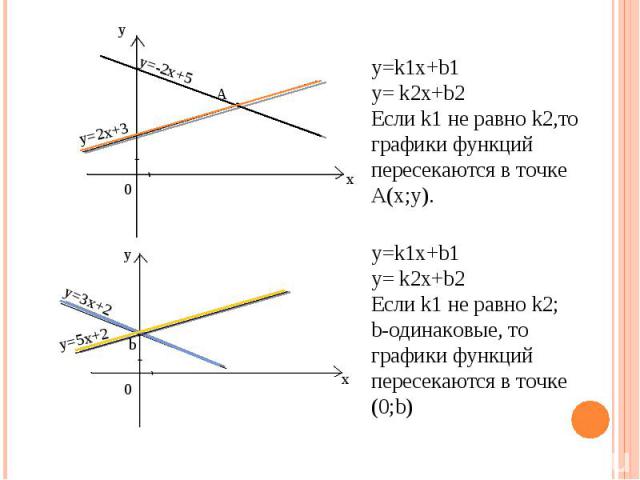
y=k1x+b1 y= k2x+b2 Если k1 не равно k2,то графики функций пересекаются в точке A(x;y). y=k1x+b1 y= k2x+b2 Если k1 не равно k2; b-одинаковые, то графики функций пересекаются в точке (0;b)

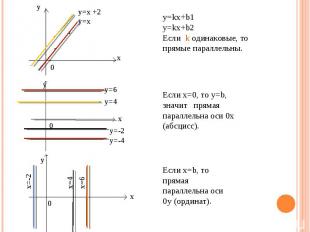
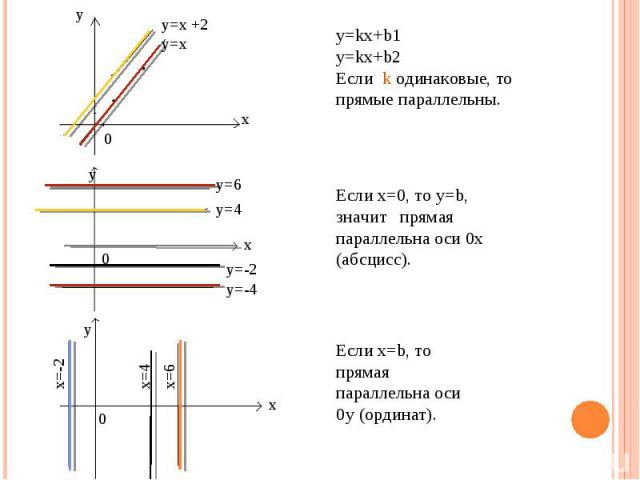
y=kx+b1 y=kx+b2 Если k одинаковые, то прямые параллельны. Если х=0, то y=b, значит прямая параллельна оси 0x (абсцисс). Если x=b, то прямая параллельна оси 0y (ординат).

Спасибо за внимание!