Презентация на тему: Взаимное расположение двух прямых

Взаимное расположение двух прямых

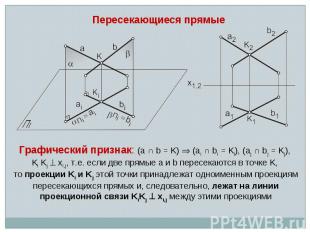
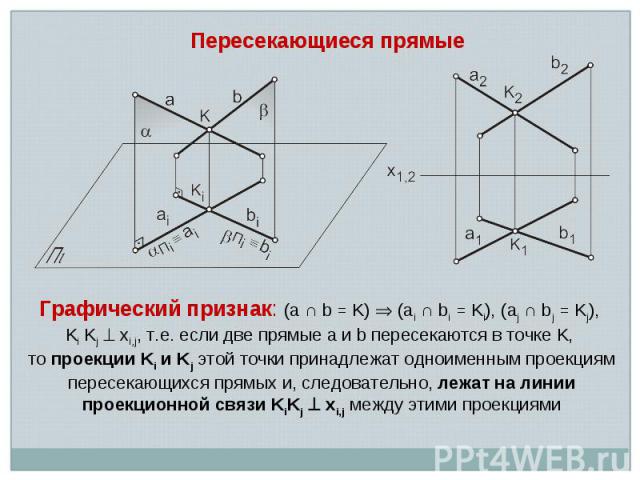
Пересекающиеся прямые Графический признак: (a ∩ b = K) (ai ∩ bi = Ki), (aj ∩ bj = Kj), Ki Kj xi,j, т.е. если две прямые a и b пересекаются в точке K, то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и, следовательно, лежат на линии проекционной связи KiKj xi,j между этими проекциями

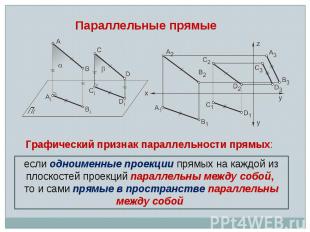
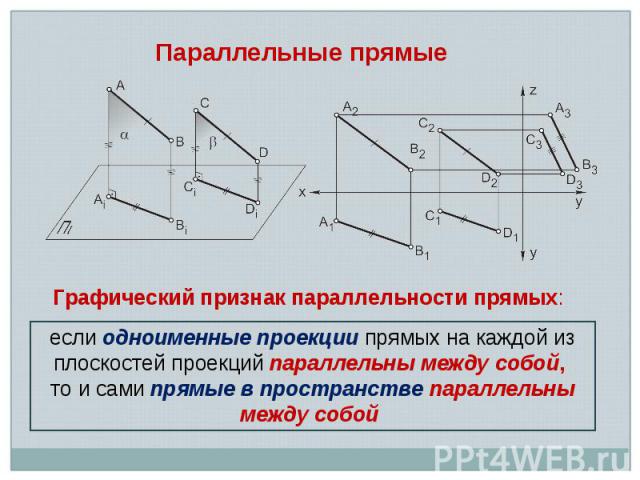
если одноименные проекции прямых на каждой из плоскостей проекций параллельны между собой, то и сами прямые в пространстве параллельны между собой Графический признак параллельности прямых: Параллельные прямые

Скрещивающиеся прямые Графический признак скрещивающихся прямых: признак основан на невыполнении признаков параллельности или пересечения таких прямых. Точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций

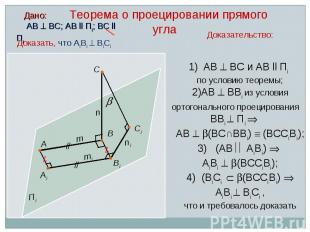
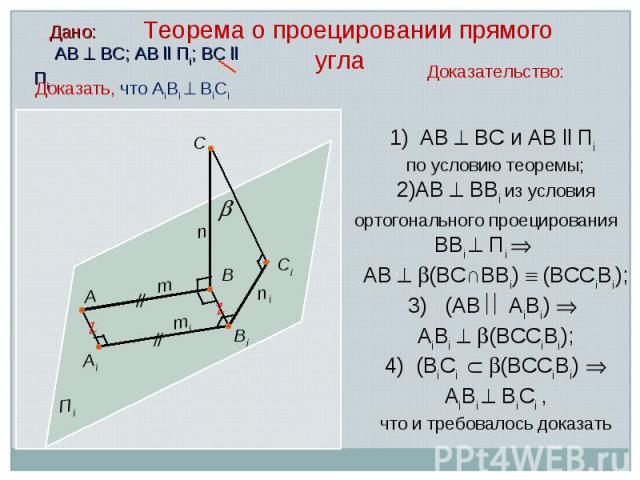
Дано: АВ ВС; АВ ll Пi; ВС ll Пi Доказательство: АВ ВС и АВ ll Пi по условию теоремы; АВ ВВi из условия ортогонального проецирования ВВi Пi АВ (ВС∩ВВi) (ВССiВi); 3) (АВ АiВi) АiВi (ВССiВi); 4) (ВiСi (ВССiВi) АiВi ВiСi , что и требовалось доказать С Аi А Вi В Сi // // Z Z mi m n ni Пi Доказать, что АiВi ВiСi Теорема о проецировании прямого угла