Презентация на тему: Бриллианты элементарной геометрии

Бриллианты элементарной геометрии

Вопросы для повторения Теорема косинусовПодобие треугольниковВписанный уголСвойство вписанных углов опирающихся на одну и туже дугу.Вписанный многоугольникФормулы приведения

Новые термины ЧЕВИАНА - отрезок соединяющий вершину треугольника с произвольной точкой противоположной стороны.ТРИСЕКТРИСА - прямые проходящие через вершину угла и делящие его на три равные части.

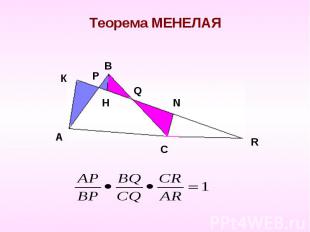
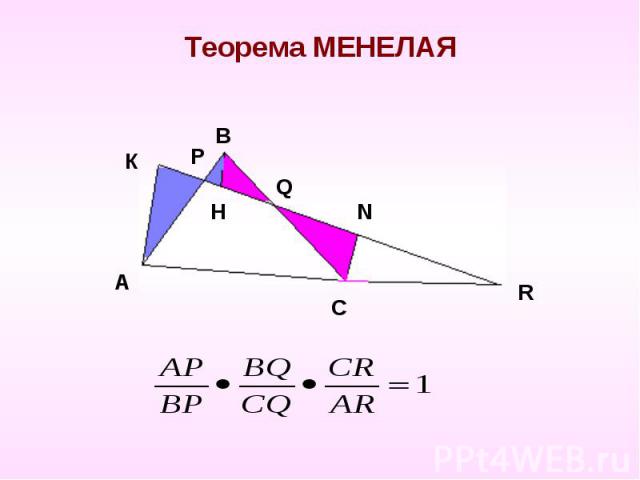
Теорема МЕНЕЛАЯ

Теорема ПаППА Теорема Паппа — это классическая теорема проективной геометрии. Она является частным случаем теоремы Паскаля. Теоремы можно сформулировать следующим образом: Пусть A, B, C — три точки на одной прямой, а A' , B' , C' — на другой. Пусть три прямые АВ' , BC' , CA' пересекают прямые A'B, B'C, C'A, соответственно в точках X, Y и Z. Тогда X, Y и Z лежат на одной прямой.

Теоремы Брахмагупта Дан произвольный 4-х угольник около которого можно описать окружность.Пусть длины его сторон a, b, c, d. Тогда площадьЕго будет вычисляться по формулеS=(p-a) (p-b) (p-c) (p-d)Если четырехугольник таков, что в него можно и вписать и описaть околоНего окружность, то его площадь может быть вычислена по формулеS=a b c d

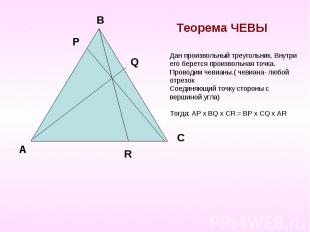
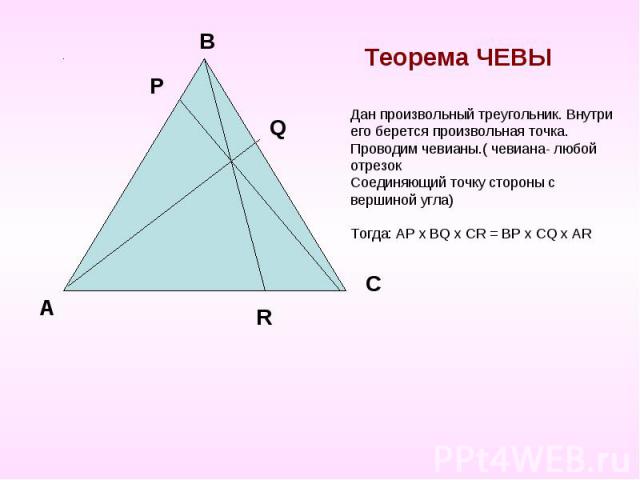
Теорема ЧЕВЫ Дан произвольный треугольник. Внутри его берется произвольная точка.Проводим чевианы.( чевиана- любой отрезокСоединяющий точку стороны с вершиной угла)Тогда: AP х ВQ х CR = BP х CQ х AR

Теорема Птолемея Пусть даны 4 точки на окружностиТогда всегда выполняется соотношение:АВ х СД + АД х ВС = АС х ВДСумма длин произведений противоположных сторон произвольного4-х угольника около которого можно описать окружность, равнаПроизведению диагоналей.

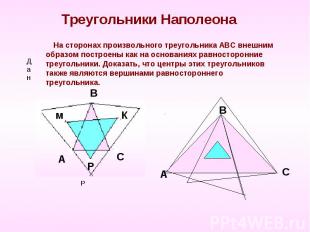
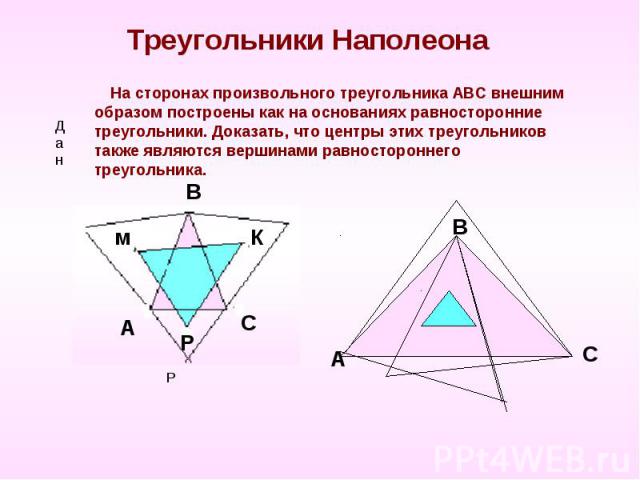
Треугольники Наполеона На сторонах произвольного треугольника АВС внешним образом построены как на основаниях равносторонние треугольники. Доказать, что центры этих треугольников также являются вершинами равностороннего треугольника.

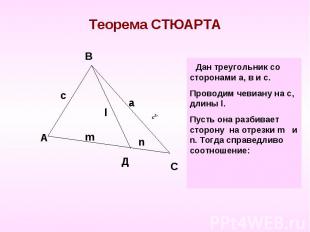
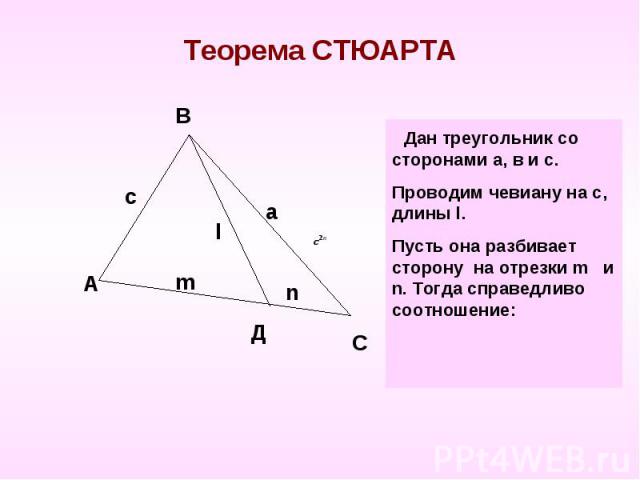
Теорема СТЮАРТА Дан треугольник со сторонами а, в и с.Проводим чевиану на с, длины l. Пусть она разбивает сторону на отрезки m и n. Тогда справедливо соотношение:

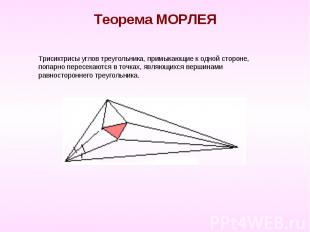
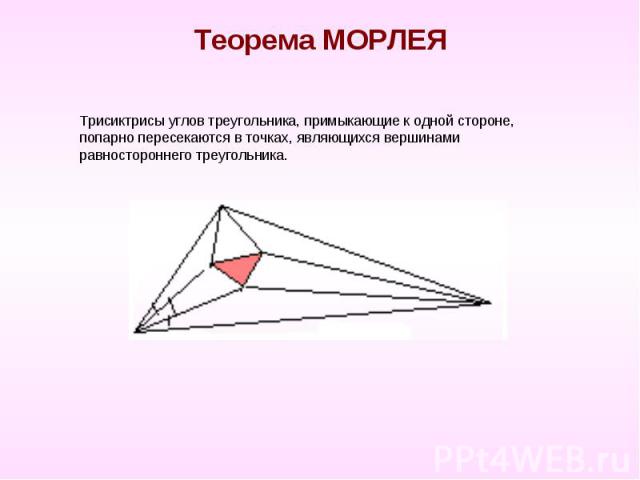
Теорема МОРЛЕЯ Трисиктрисы углов треугольника, примыкающие к одной стороне, попарно пересекаются в точках, являющихся вершинами равностороннего треугольника.

Задача Рассадите 10 деревьев в десяти рядах, так чтобы в каждом ряду былоПо 3 дерева.

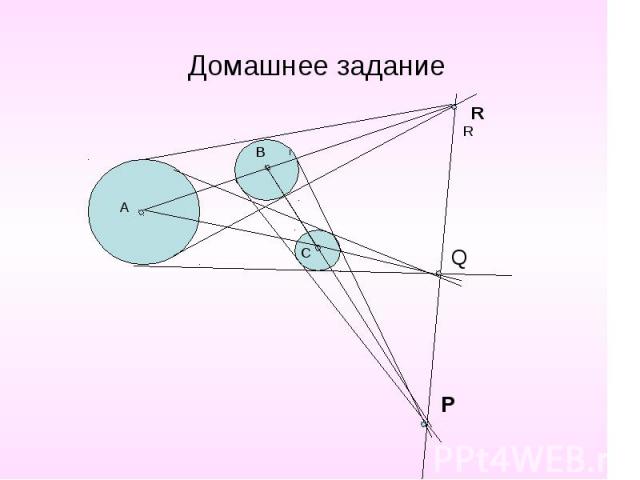
Домашнее задание