Презентация на тему: Объёмы геометрических тел и их практическое применение

Объёмы геометрических тели их практическое применение Жевачевская Анна ВалентиновнаУчитель математики/информатикиМБОУ СОШ №151г.Новосибирска

План урока Повторяем изученный материал Роль геометрии, в частности вычисления объёмов геометрических тел, в древности и в современном мире.Решение задач практического содержанияПроверь себяДомашнее задание

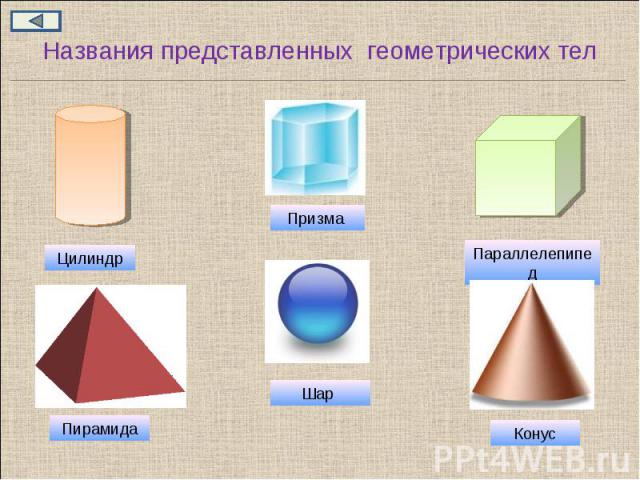
Запишите названия представленных геометрических тел

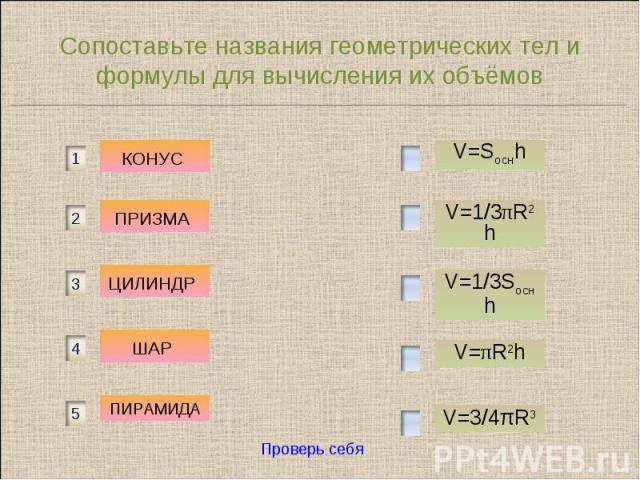
Сопоставьте названия геометрических тел и формулы для вычисления их объёмов

Заполните пропуски Равные тела имеют … объёмы. Если тело составлено из нескольких тел, то его объём равен … объёмов этих тел.Объём пирамиды равен одной трети произведения … на …. Объём … равен произведению трёх его измерений.

Практическая геометрия у древних народов Практическое применение геометрии начинается с древних времён. Египтяне использовали эту науку в различных хозяйственных работах, при сооружении оросительных каналов, грандиозных храмов и пирамид, при высечении из гранита знаменитых сфинксов и т.п. Содержащиеся в дошедших до нас папирусах геометрические сведения и задачи почти все относятся к вычислению площадей и объемов. В них нет никаких указаний на способы вывода тех правил, которыми пользовались египтяне для вычисления длин, площадей и объёмов; часто употреблялись правила приближённых подсчётов. Высшим достижением египетской геометрии следует считать точное вычисление объёма усечённой пирамиды с квадратным основанием, содержащееся в «Московском папирусе».

Геометрия и современность Велика роль геометрии и в нашем современном мире. В своей практической деятельности человек часто встречается с необходимостью вычисления объёмов, например, при изготовлении каких-либо деталей или при строительстве различных сооружений. Многие строительные объекты, детали конструкций и другие предметы имеют форму геометрических тел: параллелепипедов, призм, цилиндров, шаров и т.д.

Задача № 1 Сколько тюков сена вместится в сеновал, который имеет форму прямоугольного параллелепипеда и размеры 7 х 5 х 3 м? Тюк сена имеет размеры 36 х 50 х 90 см.

Задача № 2 Сколько тонн нефти может перевезти поезд, имеющий в своём составе 15 цистерн, если диаметр котла каждой 3м, а длина 10,8 м, а плотность нефти составляет 850 кг/м3?

Задача № 3 Пожарное ведро имеет коническую форму и предназначено для транспортировки воды и песка при локализации и ликвидации небольших загораний. Каков радиус ведра, если его объём составляет 0,01 м3 (10 л), а глубина 350 мм?

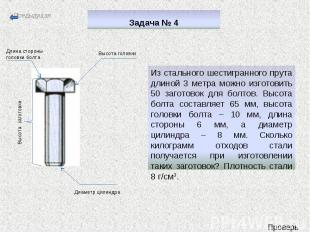
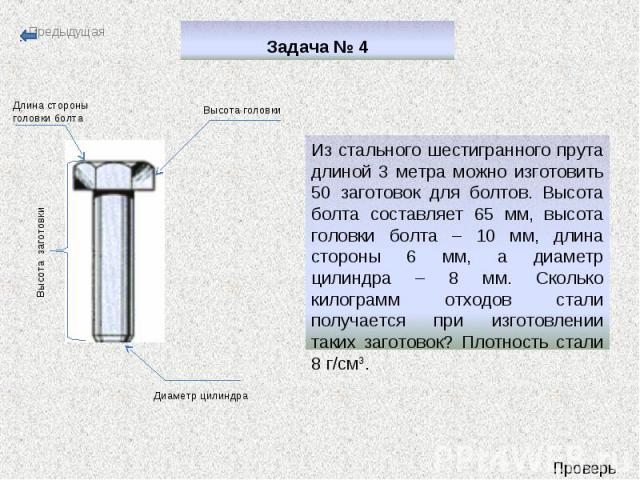
Задача № 4 Из стального шестигранного прута длиной 3 метра можно изготовить 50 заготовок для болтов. Высота болта составляет 65 мм, высота головки болта – 10 мм, длина стороны 6 мм, а диаметр цилиндра – 8 мм. Сколько килограмм отходов стали получается при изготовлении таких заготовок? Плотность стали 8 г/см3.

Домашнее задание Повторить формулы для вычисления объёмов изученных геометрических тел.Придумать и решить задачу практического содержания на вычисление объёмов геометрических тел.

Спасибо за урок !

Названия представленных геометрических тел

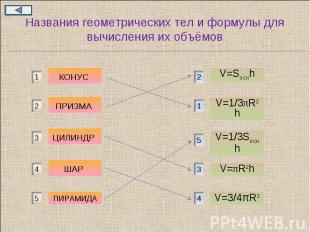
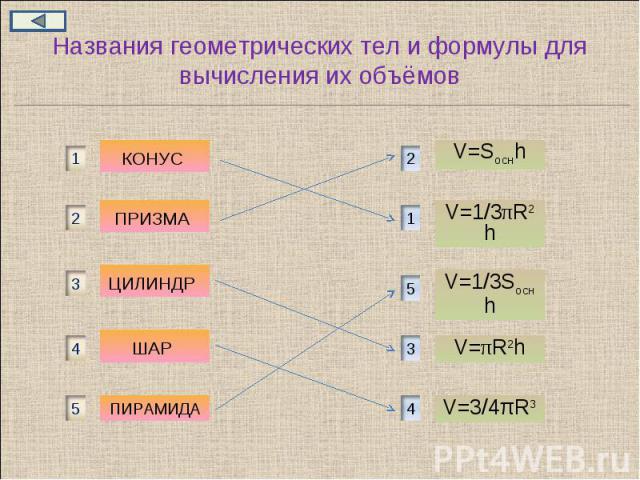
Названия геометрических тел и формулы для вычисления их объёмов

Заполните пропуски Равные тела имеют равные объёмы. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.Объём пирамиды равен одной трети произведения площади основания на высоту. Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Ответы к задачам Задача № 1.Ответ: 388 тюков Задача № 2. Ответ: 964 тонны Задача № 3. Ответ: 178 ммЗадача № 4. Ответ: 0,723 кг