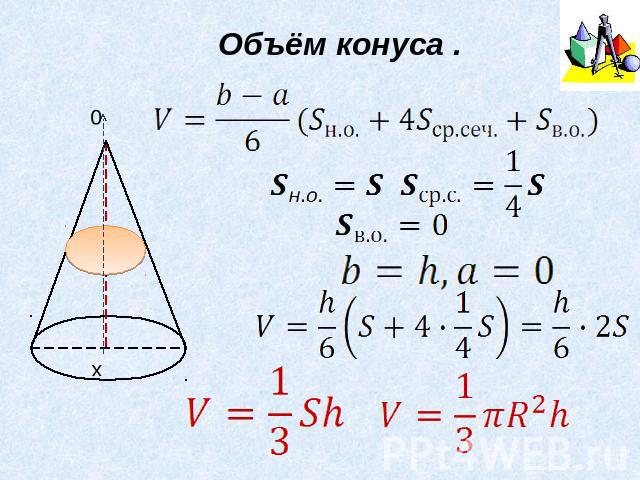Презентация на тему: Объёмы тел

МБОУ СОШ с. Камышки Тема : «Объёмы тел» Учитель: Мурзагалиева Акмоншак Хасеновна.

Если бы я родился музыкантом, Я бы стремился перебороть шумы мираС помощью стройных звуков.Если бы я родился архитектором,Я бы строил людям не квартиры, а домашние очаги.Я одарил бы их светом, цветом и тишиной,Но поскольку я поэт,Я хотел бы так же четко и ясноГоворить на языке слов, Как математики говорят на языке чисел.

Объёмы тел

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами

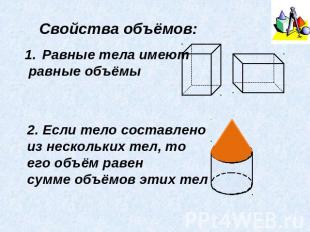
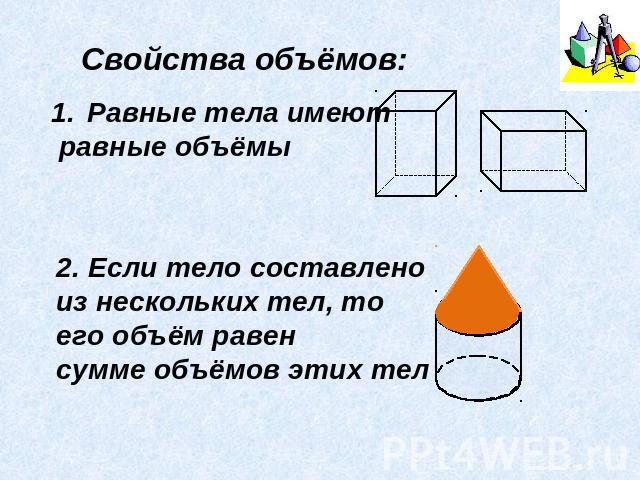
Свойства объёмов: Равные тела имеют равные объёмы Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел

Симпсон Томас - английский математик. В 1743 вывел формулу приближённого интегрирования. В 1746 году Симпсон избран в члены Лондонского королевского общества, а ранее — в члены основанного в 1717 году в Лондоне Математического общества. Назначенный профессором в Вульвич, Симсон составил учебники по элементарной математике. В особых отделах геометрии рассматриваются задачи о наибольших и наименьших величинах, решаемые с помощью элементарной геометрии, правильные многогранники, измерение поверхностей, объёмы тел и, наконец, смешанные задачи.

Формула Симпсона b, a – предельные значения высоты геометрического тела, среднее сечение – сечение тела плоскостью, параллельной основанию, и проходящей через середину высоты

Как найти объем у куба?Есть у куба 3 стены,В них по три величины.Я возьму их, перемножу.Ведь не так все это сложно.С первой стенки взял длину,Со второй взял ширину,С третьей вышла высота.Получилась красота!

Объём прямого параллелепипеда.

Объём прямой призмы.

Цилиндр, что такое? - спросил я у папы.Отец рассмеялся : - Цилиндр, это шляпа.Чтобы иметь представление верное,Цилиндр, скажем так, это банка консервная.Труба парохода- цилиндр,Труба на нашей крыше - тоже,Все трубы на цилиндр похожи.А я привёл пример такой -Калейдоскоп любимый мой,Глаз от него не оторвёшь,И тоже на цилиндр похож.

Объём цилиндра.

Я видел картину. На этой картинеСтоит ПИРАМИДА в песчаной пустыне.Всё в пирамиде необычайно,Какая-то есть в ней загадка и тайна.А Спасская башня на площади КраснойИ детям, и взрослым знакома прекрасно.Посмотришь на башню, обычная с виду,А что на вершине у ней? Пирамида!

Объём пирамиды .

Сказала мама: - А сейчасПро конус будет мой рассказ.В высокой шапке звездочётСчитает звёзды круглый год.КОНУС- шляпа звездочёта.Вот какой он. Понял? То-то.Мама у стола стоялаВ бутылки масло разливала.- Где воронка? Нет воронки.Поищи. Не стой в сторонке.-Мама, с места я не тронусь ,Расскажи ещё про конус.-Воронка и есть в виде конуса лейка.Ну-ка, найди мне её поскорей-ка.Воронку я найти не смог,Но мама сделала кулёк,Картон вкруг пальца обкрутилаИ ловко скрепкой закрепила.Масло льётся, мама рада,Конус вышел то, что надо.

Объём конуса .

Удар! Удар! Ещё удар!Летит в ворота мячик - ШАР!А это- шар арбузныйЗелёный, круглый, вкусный.Вглядитесь лучше - шар каков!Он сделан из одних кругов.Разрежьте на круги арбузИ их попробуйте на вкус.

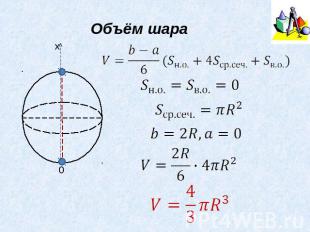
Объём шара

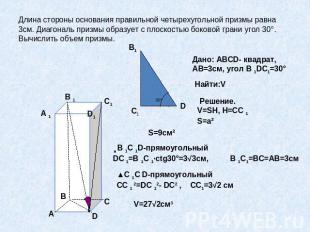
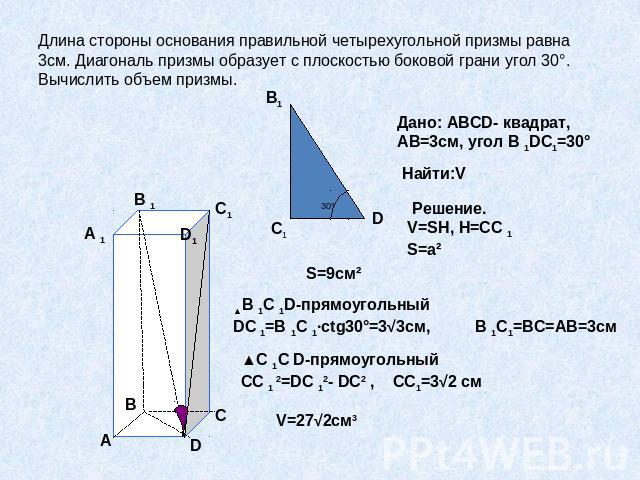
Длина стороны основания правильной четырехугольной призмы равна 3см. Диагональ призмы образует с плоскостью боковой грани угол 30°. Вычислить объем призмы.

Практическая задача. Надо найти объём воды проходящёй за день в водонапорной вышке такого типа:

Решение. Во-первых это цилиндр. Объём цилиндра равен Сложность тут может доставить нахождение радиуса, но только с практической точки зрения. R=L/2π, где L-длина окружности, которую можно измерить верёвочкой. Установив все данные, подставим в формулу объёма. Но это ещё не всё, теперь умножаем объём на количество полных закачек за день, и мы получим полный объём воды проходящей через водонапорную башню.

Задачник. №1. Найдите объём правильной четырёхугольной пирамиды, если её диагональное сечение – равносторонний треугольник, площадь которого 12 √3 №2. В правильной четырёхугольной призме ABCDA’B’C’D’ высота в два раза длиннее стороны основания. Найдите объём призмы, если расстояние между серединами рёбер A’B’ и BC равно 3√2. №3. Через две образующие конуса, угол между которыми равен 30° проведено сечение, имеющее площадь 25 дм². найти объём конуса, если радиус основания 6 дм. №4. В конус вписан шар. Найти объём шара, если радиус основания конуса равен 3, а образующая равна 4. №5. Через точку А, лежащую на окружности основания цилиндра, проведена прямая, пересекающая окружность второго основания в точке В. Радиус цилиндра равен 5, длина отрезка АВ равна 4√5, расстояние между осью цилиндра и прямой АВ равно 3. найти объём цилиндра.

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке  значения функции в соответствующих точках (на концах отрезка и в его середине). Получила название в честь британского математика Томаса Симпсона (1710—1761).

Использованы ресурсы: http://mathprofi.ru/formula_simpsona_metod_trapecij.html http://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%A1%D0%B8%D0%BC%D0%BF%D1%81%D0%BE%D0%BD%D0%B0