Презентация на тему: Объемы тел

Слайды к теме "Объемы тел"Учебник Л.С.Атанасяна «Геометрия 10-11»Учитель: Рожкова Надежда Даниловна

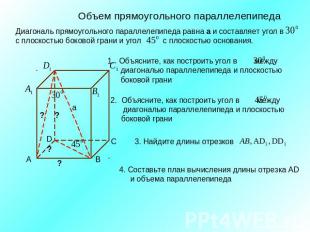
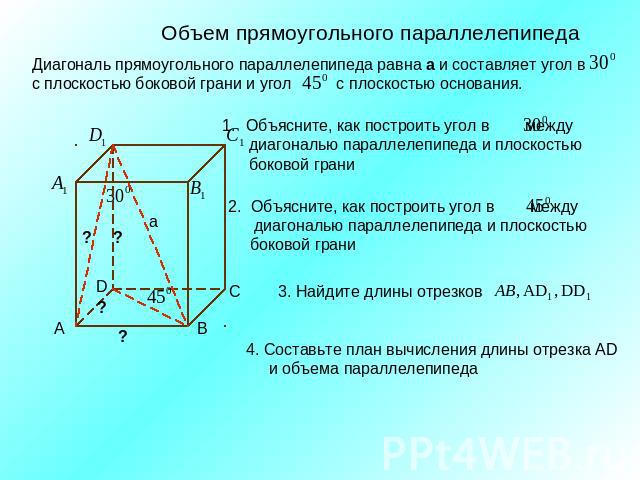
Объем прямоугольного параллелепипедаДиагональ прямоугольного параллелепипеда равна а и составляет угол в с плоскостью боковой грани и угол с плоскостью основания.Объясните, как построить угол в между диагональю параллелепипеда и плоскостью боковой граниОбъясните, как построить угол в между диагональю параллелепипеда и плоскостью боковой граниНайдите длины отрезков Составьте план вычисления длины отрезка AD и объема параллелепипеда

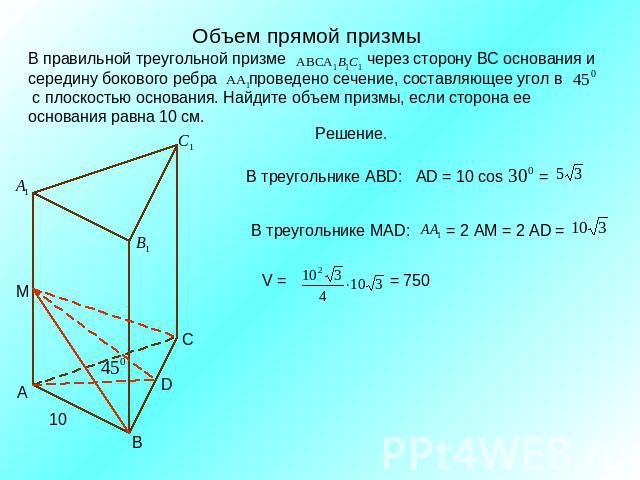
Объем прямой призмыВ правильной треугольной призме через сторону ВС основания и середину бокового ребра проведено сечение, составляющее угол в с плоскостью основания. Найдите объем призмы, если сторона ее основания равна 10 см. В треугольнике ABD: AD = 10 cos =

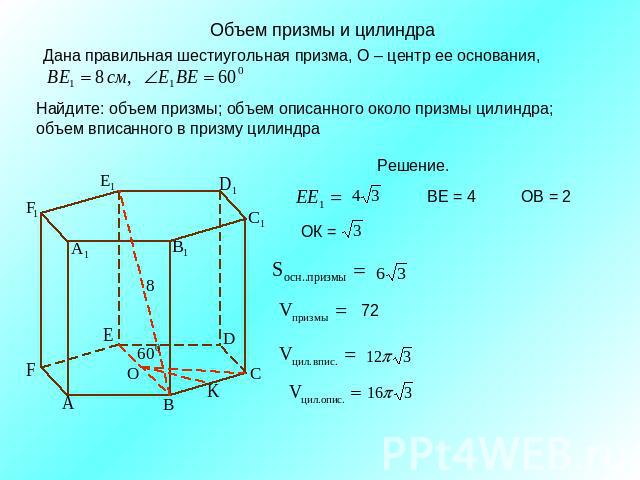
Объем призмы и цилиндраДана правильная шестиугольная призма, О – центр ее основания, Найдите: объем призмы; объем описанного около призмы цилиндра; объем вписанного в призму цилиндра

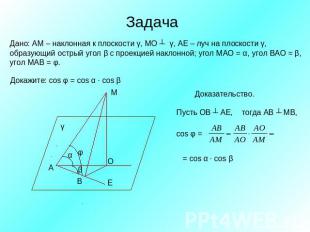
Задача Дано: АМ – наклонная к плоскости γ, МО ┴ γ, АЕ – луч на плоскости γ, образующий острый угол β с проекцией наклонной; угол МАО = α, угол ВАО = β,угол МАВ = φ.

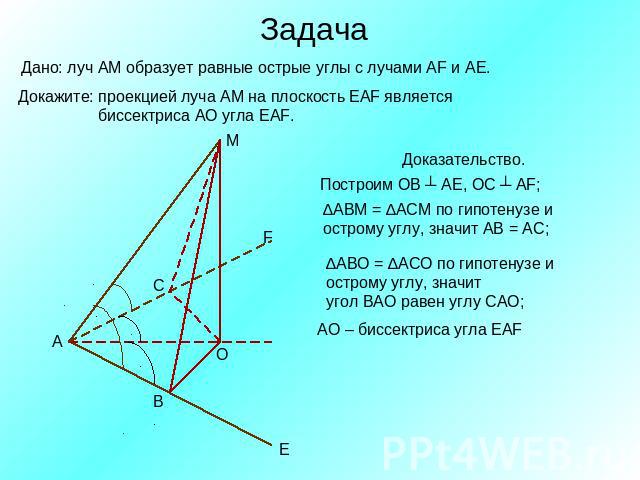
Задача Дано: луч АМ образует равные острые углы с лучами AF и АЕ. Докажите: проекцией луча АМ на плоскость EAF является биссектриса АО угла EAF.Доказательство.Построим ОВ ┴ АЕ, ОС ┴ АF; ∆АВМ = ∆АСМ по гипотенузе и острому углу, значит АВ = АС;∆АВО = ∆АСО по гипотенузе и острому углу, значит угол ВАО равен углу САО;биссектриса

Объем наклонной призмыВсе грани параллелепипеда – равные ромбы со стороной а и острым углом Найдите объем параллелепипеда.Решение.Построим проекцию ребра

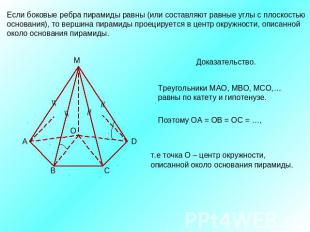
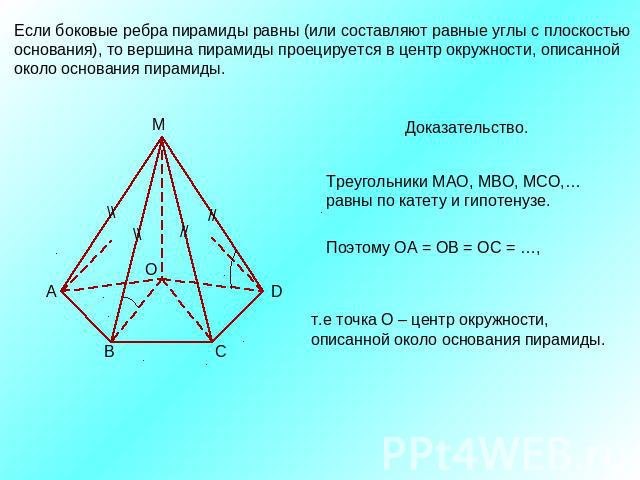
Если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описаннойоколо основания пирамиды.Доказательство.Треугольники МАО, МВО, МСО,…равны по катету и гипотенузе. т.е точка О – центр окружности,описанной около основания пирамиды.

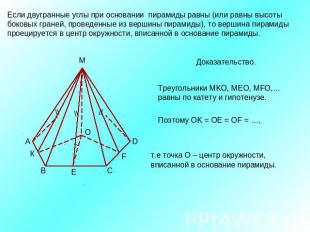
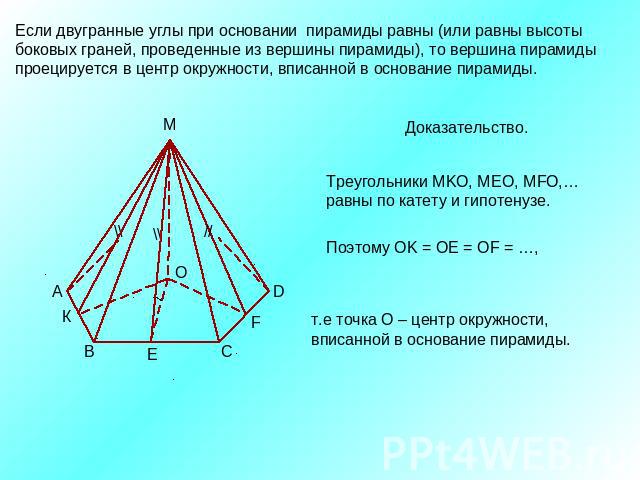
Если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.Доказательство.Треугольники МKО, МEО, МFО,…равны по катету и гипотенузе. т.е точка О – центр окружности,вписанной в основание пирамиды.

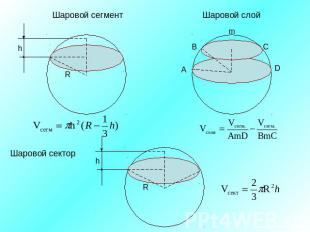
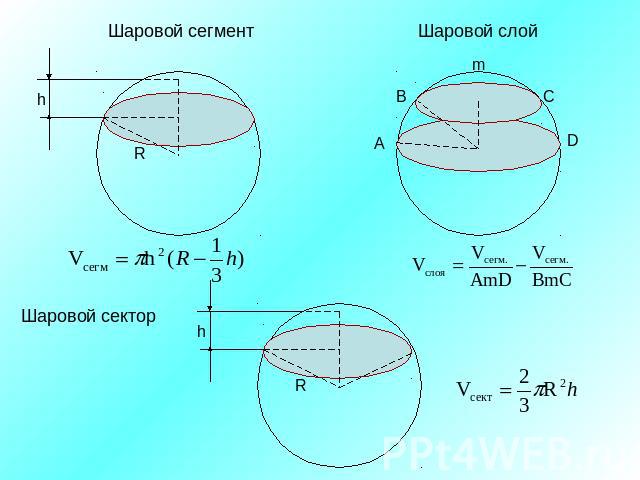
Шаровой сегментШаровой слойШаровой сектор