Презентация на тему: Графические приемы. Координатная плоскость

Графические приемы.Координатная плоскость (х;у).

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Задание№1:При каких значениях параметра а неравенство имеет единственное решение? Параллельный перенос, преобразование пространства или его части (например, переход от одной фигуры к другой), при котором все точки смещаются в одном и том же направлении на одно и то же расстояние. Совокупность всех параллельных переносов как на плоскости, так и в пространстве образует группу, которая в евклидовой геометрии является подгруппой группы движения, а в аффинной геометрии — подгруппой группы аффинных преобразований.

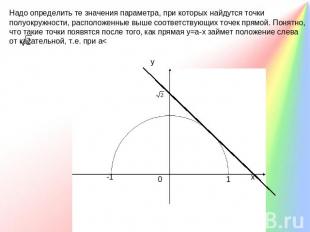
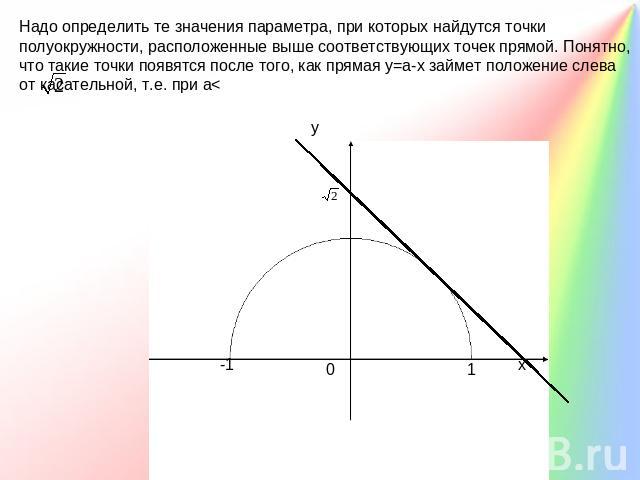
Надо определить те значения параметра, при которых найдутся точки полуокружности, расположенные выше соответствующих точек прямой. Понятно, что такие точки появятся после того, как прямая у=а-х займет положение слева от касательной, т.е. при а<

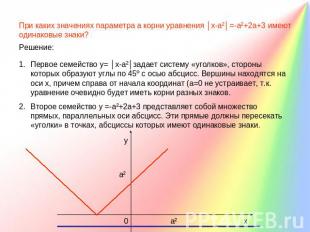
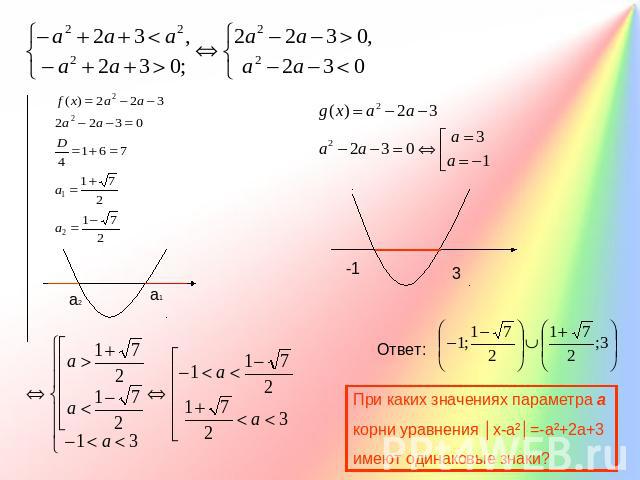
При каких значениях параметра а корни уравнения │х-а²│=-а²+2а+3 имеют одинаковые знаки? Первое семейство у= │х-а²│задает систему «уголков», стороны которых образуют углы по 45º с осью абсцисс. Вершины находятся на оси х, причем справа от начала координат (а=0 не устраивает, т.к. уравнение очевидно будет иметь корни разных знаков.Второе семейство у =-а²+2а+3 представляет собой множество прямых, параллельных оси абсцисс. Эти прямые должны пересекать «уголки» в точках, абсциссы которых имеют одинаковые знаки.

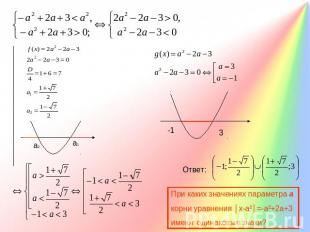
При каких значениях параметра а корни уравнения │х-а²│=-а²+2а+3 имеют одинаковые знаки?