Презентация на тему: Осевая и центральная симметрии 8 класс

Осевая и центральная симметрии. Геометрия, 8 класс.

Осевая симметрия. Две точки А и В называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АВ и перпендикулярна к нему. АО = ВО, АВ а Точка С симметрична сама себе относительно прямой а. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадле-жит этой фигуре. Прямая а называется осью симметрии фигуры.

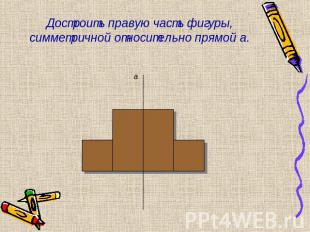
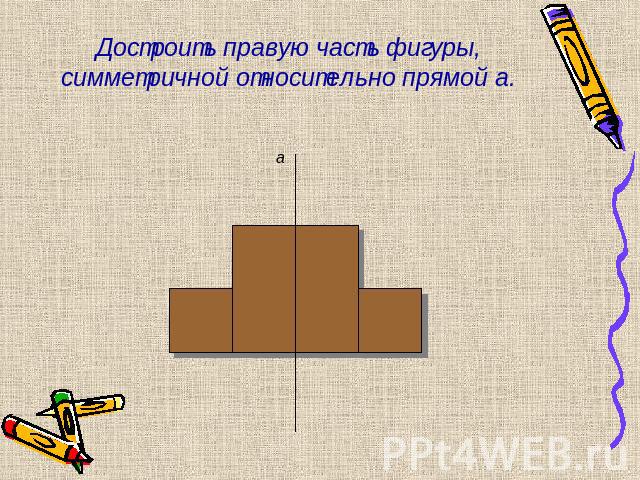
Достроить правую часть фигуры, симметричной относительно прямой а.

Какие из следующих букв имеют ось симметрии?

Центральная симметрия.Симметрия относительно точки. Точки А и М называются симметричными относительно точки О, если точка О – середина отрезка АМ.Точка О, симметричная сама себе, называется центром симметрии.АО = ОМФигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.Точка О – центр симметрии фигуры.

Достроить фигуру, обладающую центральной симметрией.

Имеют ли центр симметрии: отрезок,луч,пара пересекающихся прямых,квадрат?

Домашнее задание. Пункт 47, конспект.№ 421, 416,подготовить макет по центральной и осевой симметрии.