Презентация на тему: Симметрия. Осевая и центральная симметрии

Урок по геометриив 8 классе Симметрия. Осевая и центральная симметрии

Я в листочке, я в кристалле,Я в живописи, архитектуре,Я в геометрии, я в человеке.Одним я нравлюсь, другиеНаходят меня скучной.Но все признают, что Я - элемент красоты.

Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность».Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство. Герман Вейль.
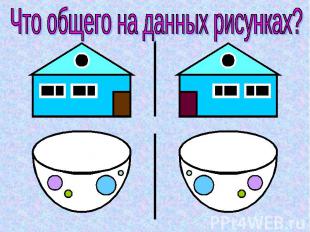
Что общего на данных рисунках?
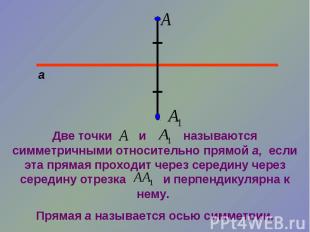
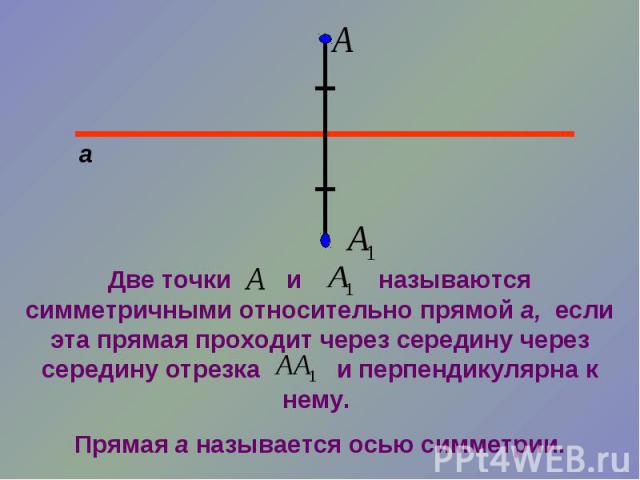
Две точки и называются симметричными относительно прямой а, если эта прямая проходит через середину через середину отрезка и перпендикулярна к нему. Прямая а называется осью симметрии.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
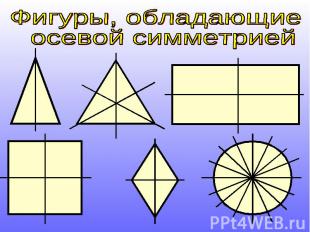
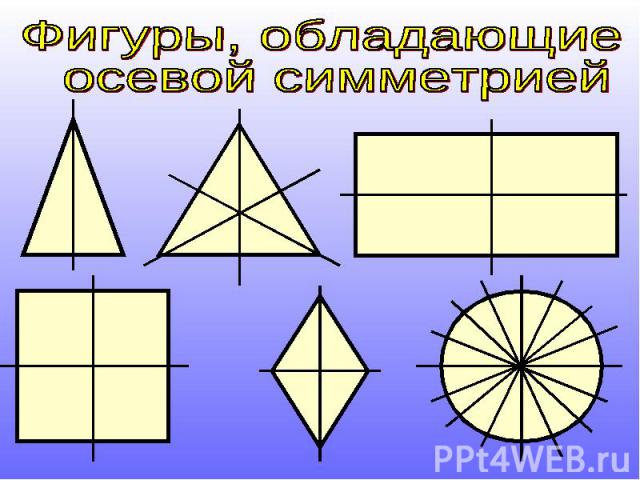
Фигуры, обладающие осевой симметрией

Буквы, имеющие горизонтальную ось симметрииВ Е Ж З К Н О С Ф Х Э Ю

Буквы, имеющие вертикальную ось симметрииА Д Ж Л М Н О П Т Ф Х Ш

Буквы, не имеющие ось симметрииБ Г И Р У Ц Ч Я Щ

Симметрия широко распространена в природе

Издавна человек использовал симметрию в архитектуре

Здание МГУ им. М. В. ЛомоносоваЗдание Большого театра в Москве

Многие атомы располагаются в пространстве по принципу симметрииКристаллы блещут симметрией Е. С. Федоров (кристаллограф)

Две точки и называются симметричными относительно точки О, если О – середина отрезка .Точка О – называется центром симметрии
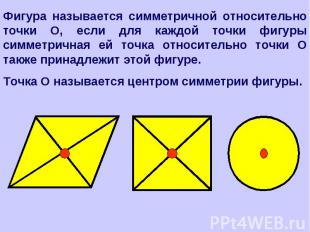
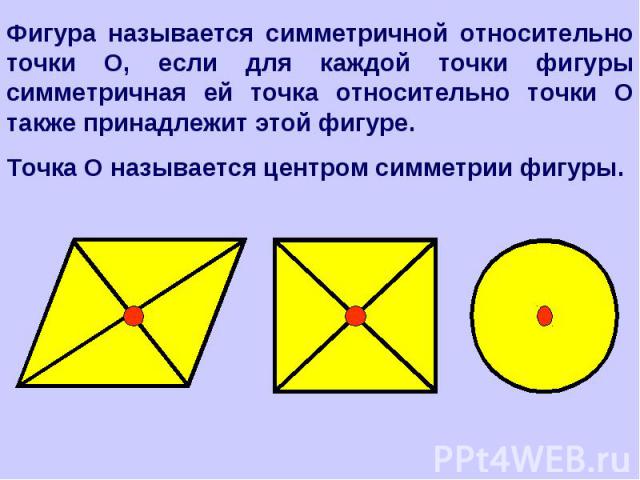
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.Точка О называется центром симметрии фигуры.
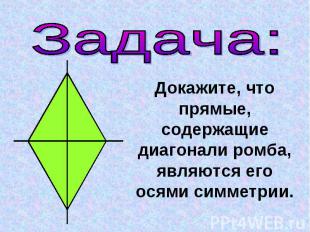
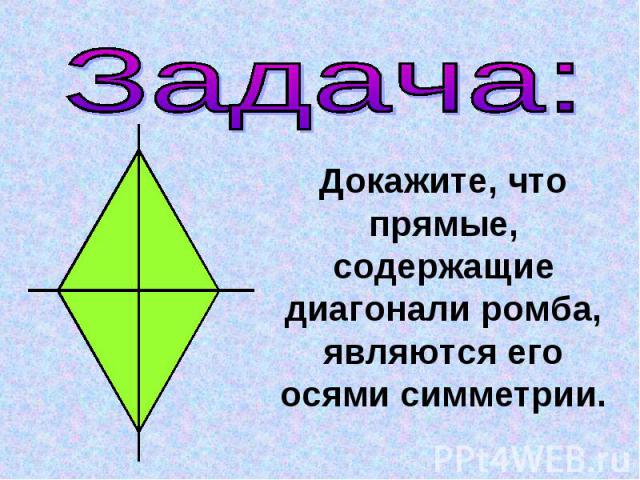
Задача:Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.

Задача:Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.

Задача:Сколько осей симметрии имеет пара параллельных прямых?