Презентация на тему: Прямые. Скрещивающиеся
Прямые. Скрещивающиеся

Ребята! Сегодня мы с вами выходим в открытое пространство. Объект изучения – скрещивающиеся прямые. Вы конечно помните, что две прямые называются скрещивающимися, если они не лежат в одной плоскости. Давайте посмотрим какими еще интересными свойствами обладают скрещивающиеся прямые.
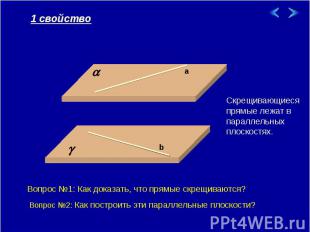
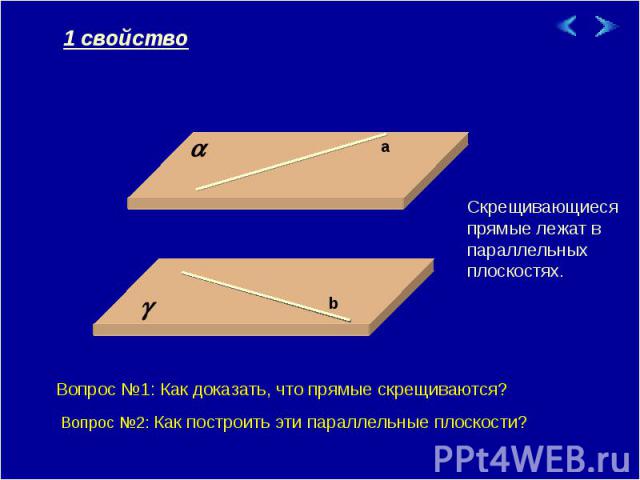
1 свойство Скрещивающиеся прямые лежат в параллельных плоскостях. Вопрос №1: Как доказать, что прямые скрещиваются? Вопрос №2: Как построить эти параллельные плоскости?
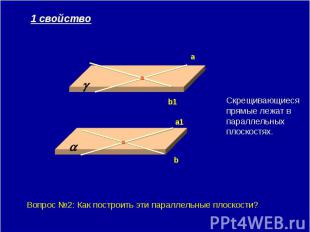
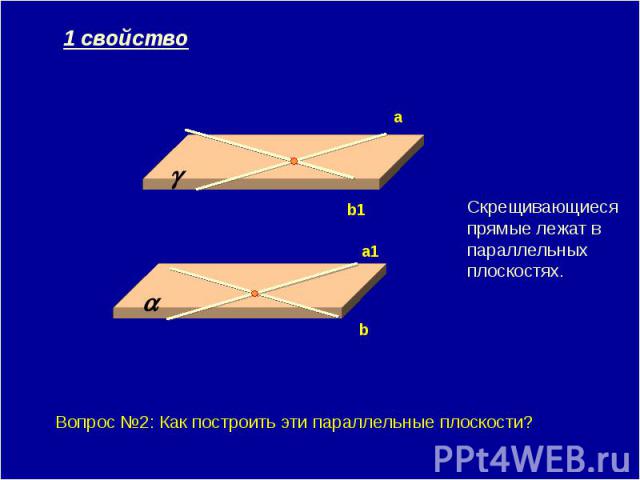
1 свойство Скрещивающиеся прямые лежат в параллельных плоскостях. Вопрос №2: Как построить эти параллельные плоскости?
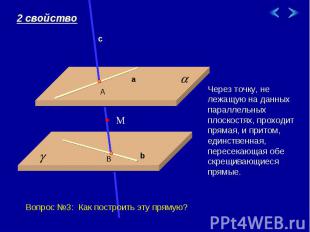
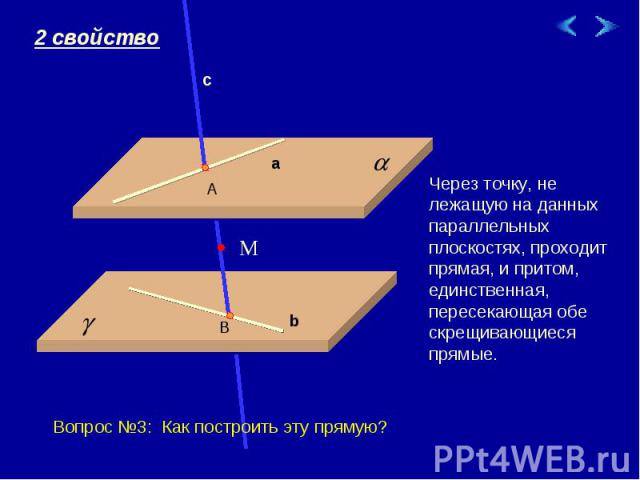
Через точку, не лежащую на данных параллельных плоскостях, проходит прямая, и притом, единственная, пересекающая обе скрещивающиеся прямые. Вопрос №3: Как построить эту прямую?
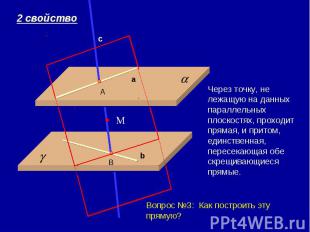
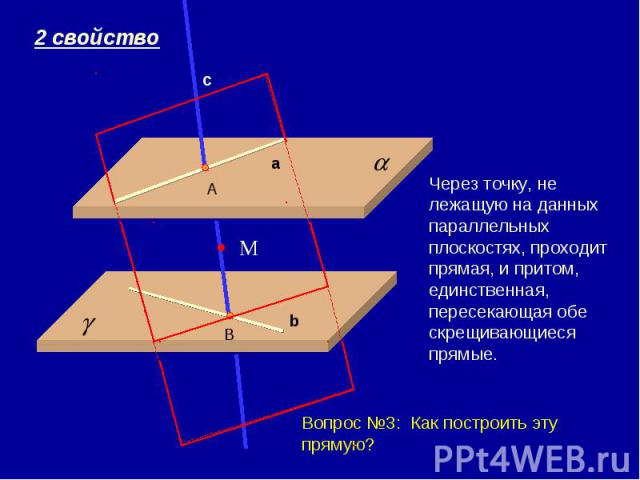
Через точку, не лежащую на данных параллельных плоскостях, проходит прямая, и притом, единственная, пересекающая обе скрещивающиеся прямые. Вопрос №3: Как построить эту прямую?
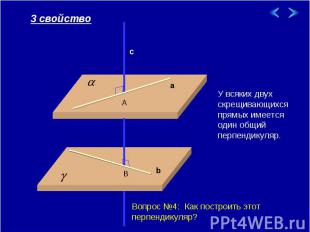
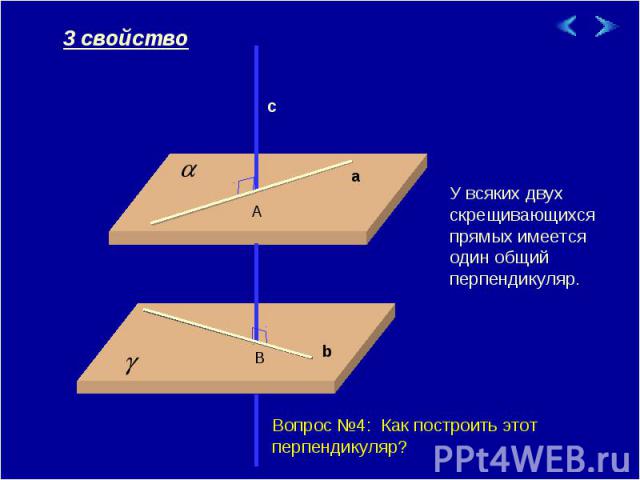
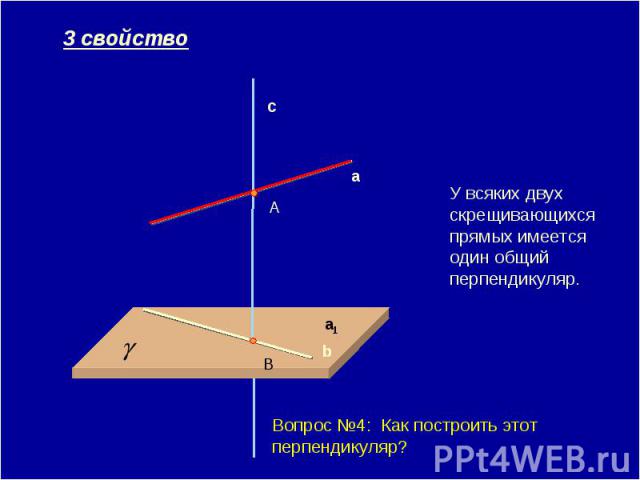
У всяких двух скрещивающихся прямых имеется один общий перпендикуляр. Вопрос №4: Как построить этот перпендикуляр?
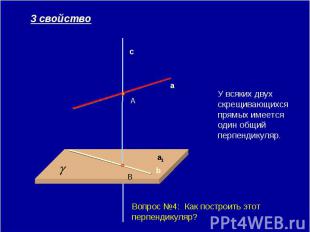
У всяких двух скрещивающихся прямых имеется один общий перпендикуляр. Вопрос №4: Как построить этот перпендикуляр?

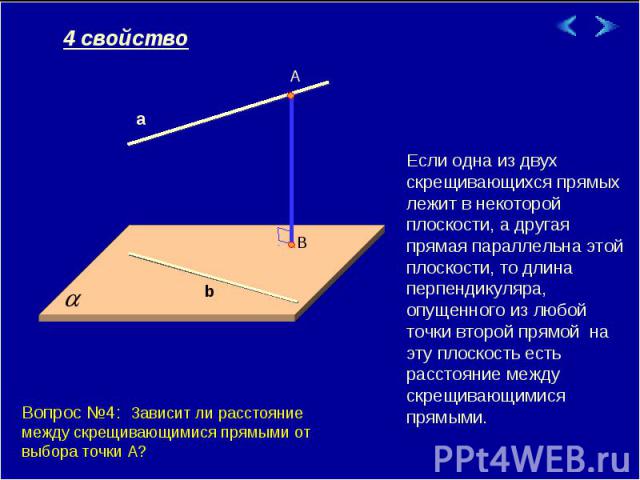
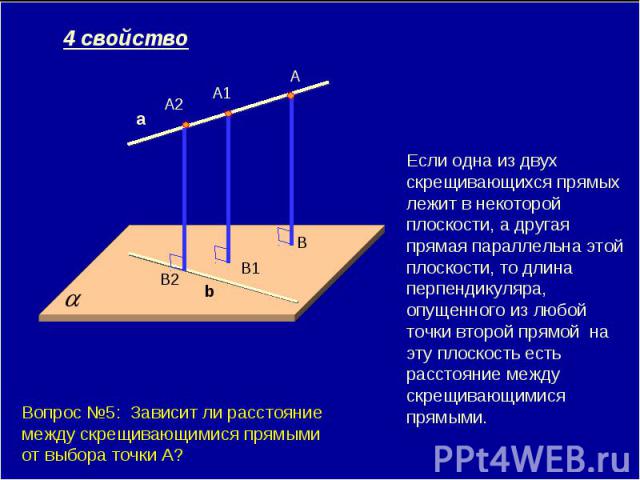
Если одна из двух скрещивающихся прямых лежит в некоторой плоскости, а другая прямая параллельна этой плоскости, то длина перпендикуляра, опущенного из любой точки второй прямой на эту плоскость есть расстояние между скрещивающимися прямыми. Вопрос №4: Зависит ли расстояние между скрещивающимися прямыми от выбора точки А?
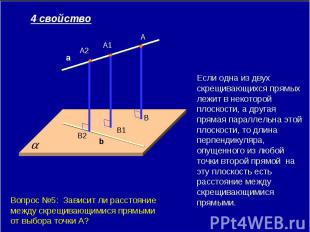
Если одна из двух скрещивающихся прямых лежит в некоторой плоскости, а другая прямая параллельна этой плоскости, то длина перпендикуляра, опущенного из любой точки второй прямой на эту плоскость есть расстояние между скрещивающимися прямыми. Вопрос №5: Зависит ли расстояние между скрещивающимися прямыми от выбора точки А?

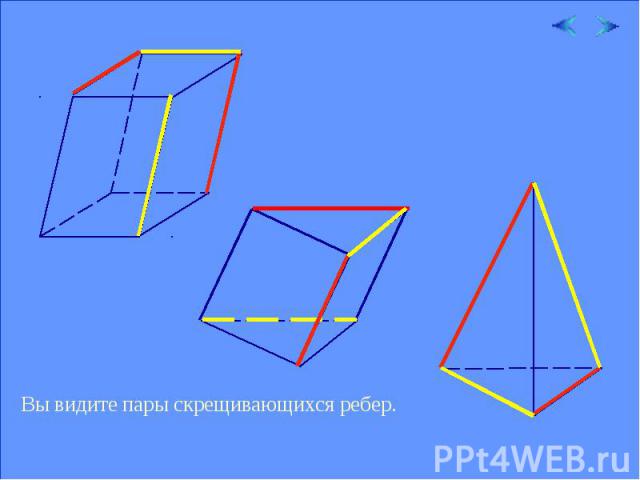
Теперь вы догадываетесь, какие интересные конструкции можно составлять из скрещивающихся прямых. Без скрещивающихся ребер нет и многогранника. Рассмотрим несколько моделей различных многогранников.
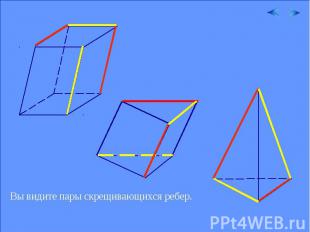
Вы видите пары скрещивающихся ребер.
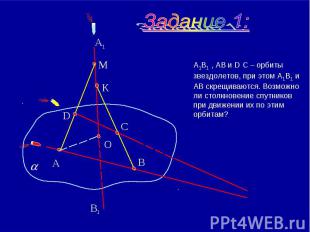
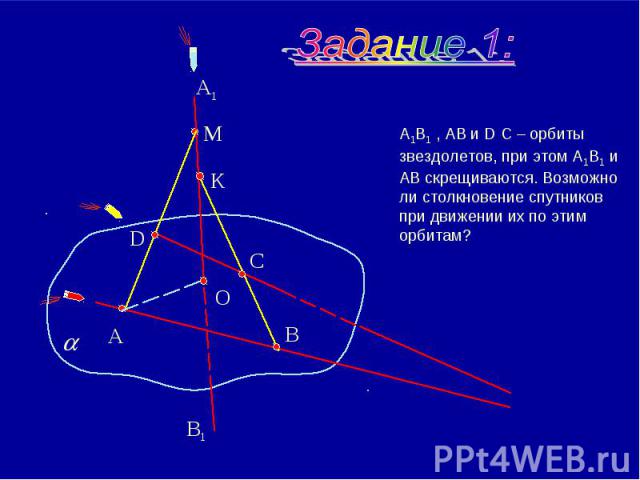
А1В1 , АВ и D С – орбиты звездолетов, при этом А1В1 и АВ скрещиваются. Возможно ли столкновение спутников при движении их по этим орбитам?
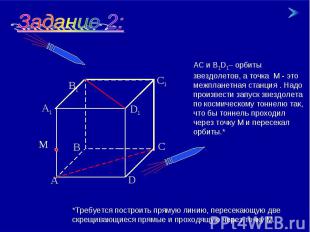
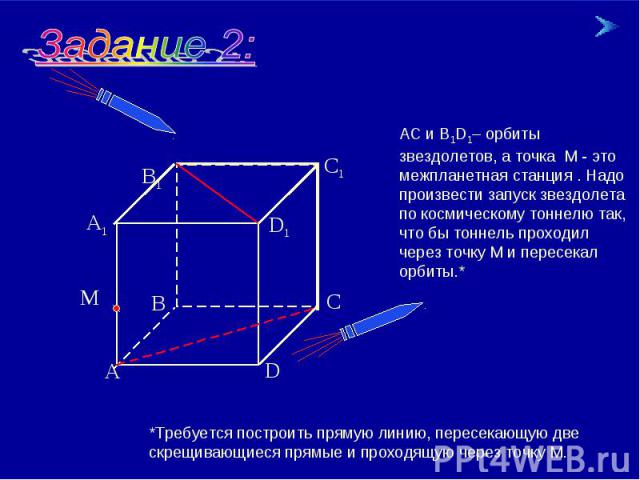
АС и В1D1– орбиты звездолетов, а точка М - это межпланетная станция . Надо произвести запуск звездолета по космическому тоннелю так, что бы тоннель проходил через точку М и пересекал орбиты.* *Требуется построить прямую линию, пересекающую две скрещивающиеся прямые и проходящую через точку М.
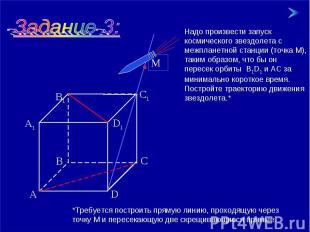
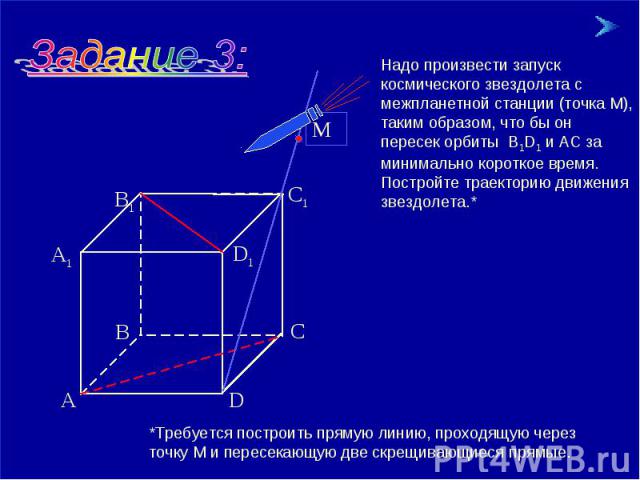
Надо произвести запуск космического звездолета с межпланетной станции (точка М), таким образом, что бы он пересек орбиты В1D1 и АС за минимально короткое время. Постройте траекторию движения звездолета.* *Требуется построить прямую линию, проходящую через точку М и пересекающую две скрещивающиеся прямые.
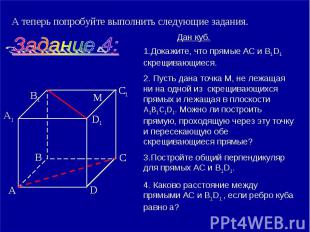
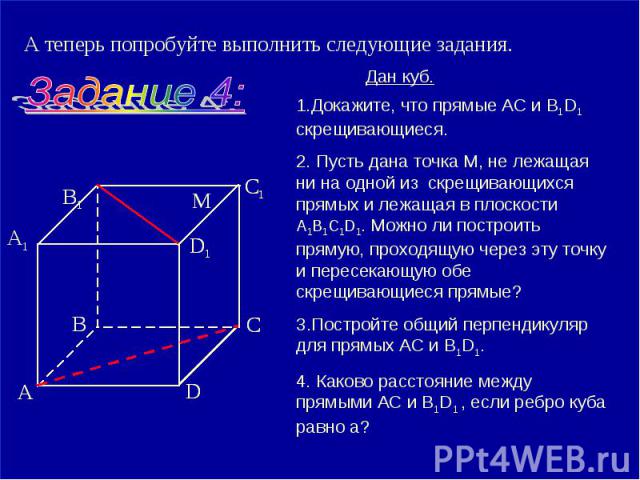
А теперь попробуйте выполнить следующие задания. 1.Докажите, что прямые АС и B1D1 скрещивающиеся. 2. Пусть дана точка М, не лежащая ни на одной из скрещивающихся прямых и лежащая в плоскости А1В1С1D1. Можно ли построить прямую, проходящую через эту точку и пересекающую обе скрещивающиеся прямые?3.Постройте общий перпендикуляр для прямых АС и B1D1.4. Каково расстояние между прямыми АС и В1D1 , если ребро куба равно а?

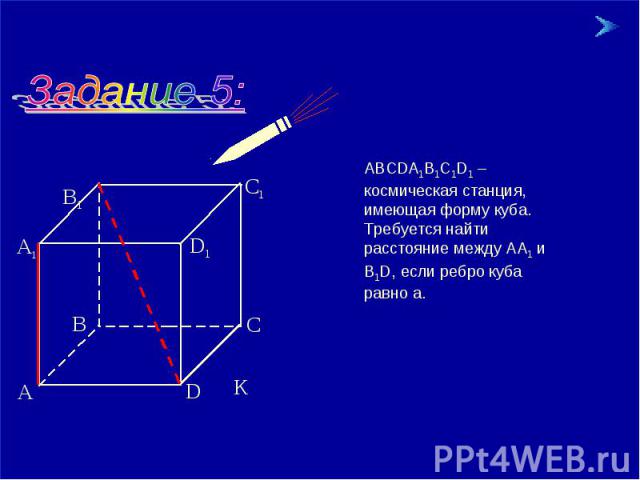
АВСDА1В1С1D1 – космическая станция, имеющая форму куба. Требуется найти расстояние между АА1 и В1D, если ребро куба равно а.

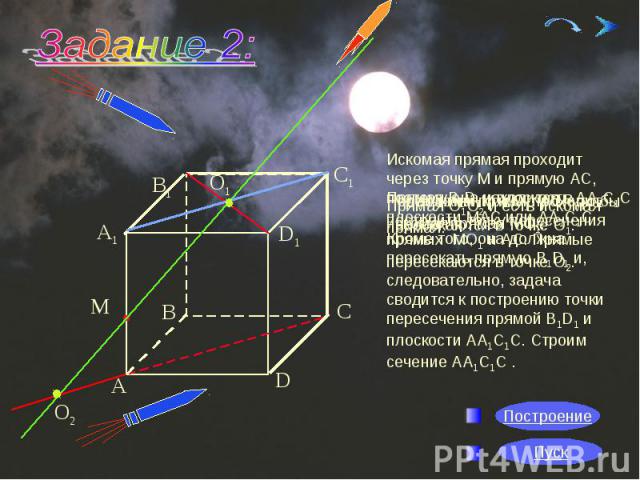
Искомая прямая проходит через точку М и прямую АС, поэтому она находится в плоскости МАС или АА1С1С. Кроме того, она должна пересекать прямую В1D1 и, следовательно, задача сводится к построению точки пересечения прямой В1D1 и плоскости АА1С1С. Строим сечение АА1С1С .
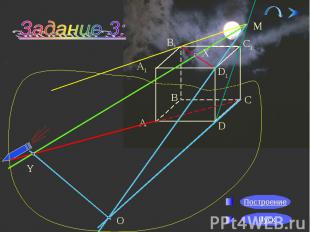
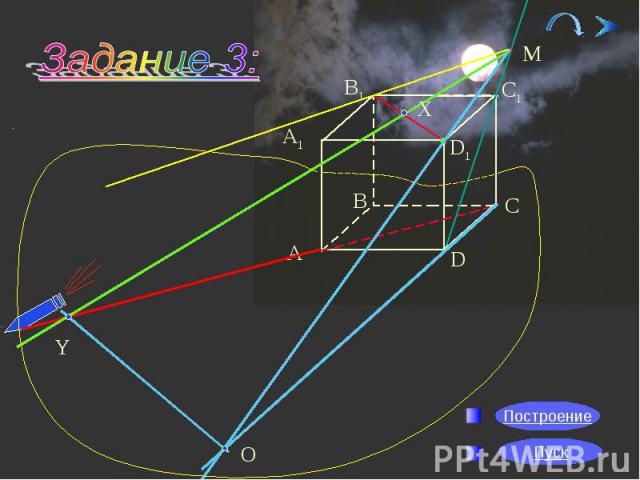
Задание 3:

Замечаем, что прямая В1D лежит в плоскости сечения ВВ1D1D, а прямая АА1 параллельна этой плоскости. Следовательно, что бы найти расстояние между прямыми АА1 и В1D надо опустить перпендикуляр из любой точки прямой АА1 на плоскость ВВ1D и найти его длину. АО и есть искомое расстояние.

Т.к. прямые лежат в параллельных плоскостях, то они не пересекаются, а т.к. они не параллельны. Следовательно они скрещиваются.Надо на одной из скрещивающихся прямых отметить произвольную точку и построить через эту точку прямую, параллельную второй скрещивающейся прямой. Затем через две пересекающиеся прямые построить 1-ю плоскость. Аналогичным образом поступить со второй плоскостью. (признак параллельности двух плоскостей).Надо через одну из скрещивающихся прямых и данную точку построить плоскость. Вторая из скрещивающихся прямых будет пересекать эту плоскость в некоторой точке. Через эту точку и данную точку провести искомую прямую.Надо через одну из скрещивающихся прямых провести плоскость, параллельную второй прямой и затем параллельным переносом опустить вторую прямую на эту плоскость, что бы найти точку пересечения прямых. Из этой точки восстановить перпендикуляр на вторую прямую.Нет.

Наше путешествие закончилось, но никогда не кончатся удивительные открытия, которые вам предстоят при дальнейшем изучении стереометрии.