Презентация на тему: Параллелограмм Вариньона

Параллелограмм Вариньона

Вариньон Пьер (1654-22.12.1722,Париж)Французский математик и механик. Член Французской АН с (1688).Родился в Каенне. Изучал философию и математику. С 1688-профессор математики в Коллеже Мазарини, с 1704-Коллеж де Франс.

Основные работы относятся к геометрии и статике. Исходя из теории сложных движений сформулировал (ок. 1710) закон параллелограмма сил. Развил понятие момента сил и предложил геометрическое доказательство теоремы о том, что момент равнодействующей двух сходящихся сил равен сумме моментов составляющих сил (теорема Вариньона).Установил (1687) теорему о скользящих векторах для случая сходящейся системы сил. Одним из первых начал пользоваться математическим анализом. Изучал равновесие и движение жидкости. Дал объяснение закона Торричелли. Полагая, что вес колонны воды пропорционален высоте h, нашёл выражение для закона Торричелли.

Описание работы Мы провели исследование по теме: «Параллелограмм Вариньона»Сформулировали определение четырёхугольника Вариньона. Доказали свойство: «четырёхугольник Вариньона является параллелограммом».Определили вид параллелограмма Вариньона для различных видов четырёхугольников.

Доказали свойство площади параллелограмма Вариньона.Доказали свойство: «Многоугольник Вариньона для правильного многоугольника также является правильным.Заключение. Подобрали 7 задач, в которых использовали теоретический материал работы.

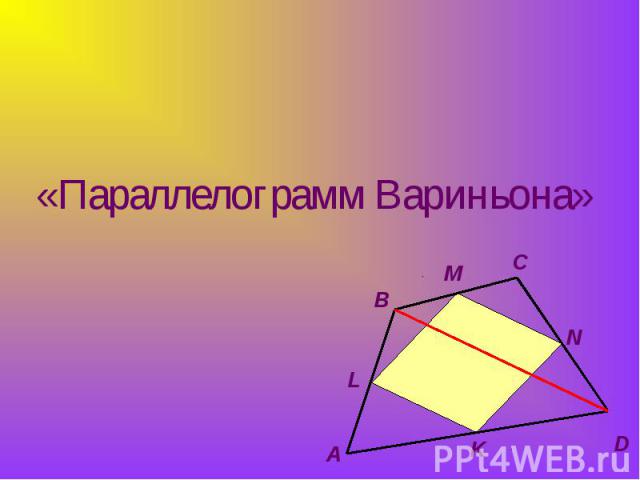
Параллелограмм Вариньона -это четырёхугольник с вершинами в серединах сторон данного четырёхугольника.Свойство площади параллелограмма Вариньонатеорема: площадь параллелограмма Вариньона равна половине площади данного четырёхугольника.

Пусть S- площадь данного четырехугольника ABCD, s-площадь четырехугольника KLMN , вершины которого- K, L, M, и N середины сторон AB, BC, CD и AD соответственно.Поскольку KL и MN- средние линии треугольников ABC и ADC, то S▲DLK=1/4 S▲ADC; S▲BMN=1/4 ▲ABC,Поэтому:S▲DLK+S▲BMN=1/4S▲ABC+1/4S▲ADC==1/4(S▲ABC +S▲ADC)=1/4SАналогично:S▲KNC+S▲MAL=1/4 SСледовательно, s=S-S▲DLK-S▲MBN-S▲LAM-S▲NCK=S-1/4S-1/4S=1/2S

Определим вид параллелограмма Вариньона для ромба Дано: АBCD-ромб.Определить вид параллелограмма Вариньона. 1.Рассмотрим ▲ABDLE-средняя линияТ.е получим, что EL║BD, и EL=1/2BD2. Аналогично, рассматривая ▲BCD получим, что FK║BD, FK=1/2 BDТо есть EL=FK; EL║FK, значит четырёхугольник EFKL является параллелограммом, так как две противолежащие стороны четырёхугольника равны и параллельны. А так как диагонали ромба пересекаются под прямым углом, то и параллельные им стороны четырёхугольникабудут тоже пересекаться под прямым углом.Следовательно, если исходной фигурой является ромб, то параллелограмм Вариньона принимает вид прямоугольника.

Определили вид параллелограмма Вариньона для различных видов четырёхугольников Для прямоугольникаДля равнобокой трапецииДля квадрата

Мы подобрали и решили 7 задач, где использовали теоретический материал нашей исследовательской работы.

Хотелось бы представить вашему вниманию одну из решённых задач: ABCD- прямоугольник, M, K, P и T- середины его сторон, AB=6см, AD=12см.Найти площадь четырехугольника MKPT.Решение: MKPT является параллелограммом Вариньона. Используя свойство площади параллелограмма Вариньона: площадь параллелограмма Вариньона равна половине площади данного четырехугольника, получим:Площадь MKPT=1/2 площади ABCD => S=1/2 • 6•12=36(кв.см)Ответ: 36(кв.см)

Мы рассмотрели вопросы, связанные с теоремами о параллелограмме Вариньона, и нашли их широкое практическое применение при решении задач.Эти знания позволили нам более глубоко познакомиться с данным материалом, и применять их в нестандартных ситуациях. Поиск новой информации из различных печатных источников, а так же из сети Интернет расширил наши знания по предмету геометрии. Мы смогли попробовать себя в новой ситуации, когда знания приобретались нами самостоятельно без помощи учителя, а это в свою очередь позволило нам поверить в себя и в свои возможности. Намеченный нами план был выполнен, и мы планируем продолжить нашу исследовательскую работу на тему «Дельтоид», где будут использоваться полученные нами знания.

Мы пользовались следующей литературой : Сборник тестовых заданий по геометрии 9 класс, «Интеллект-Центр» Москва 2001.Задачи по геометрии 7-11кл., авторы: Б. Г. Зив, В. М. Мейлер, А. Г. Баханский.Научный журнал «Математика в школе». Материалы из сети Интернет «Система задач по геометрии Р. К. Гордина».