Презентация на тему: Нахождение площадей параллелограмма, ромба

Нахождение площадей параллелограмма, ромба. Цель урока: Умение вычислять площади параллелограмма, ромба Задачи урока: Учебно-познавательная: формирование умения вычислять площади нестандартных фигур, параллелограмма и ромба. Развивающая: развитие умений самостоятельно работать с дополнительными материалами, провести самооценку учебной деятельности на уроке; Воспитательная: воспитание настойчивости и трудолюбия.

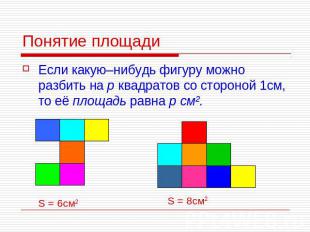
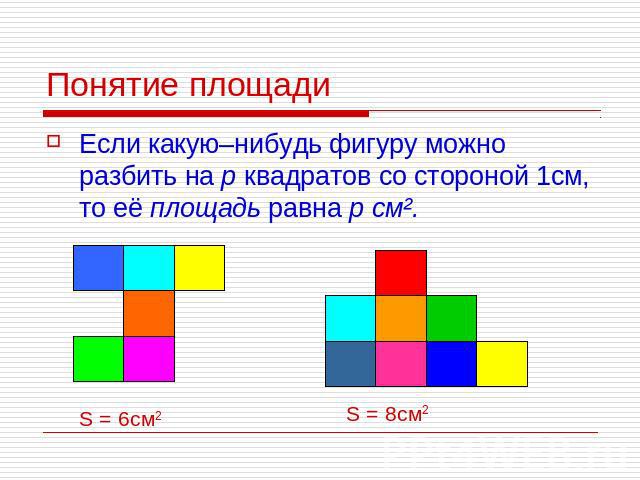
Понятие площади Если какую–нибудь фигуру можно разбить на р квадратов со стороной 1см, то её площадь равна р см². S = 6см2 S = 8см2

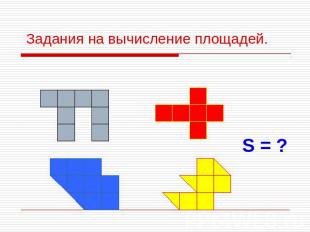
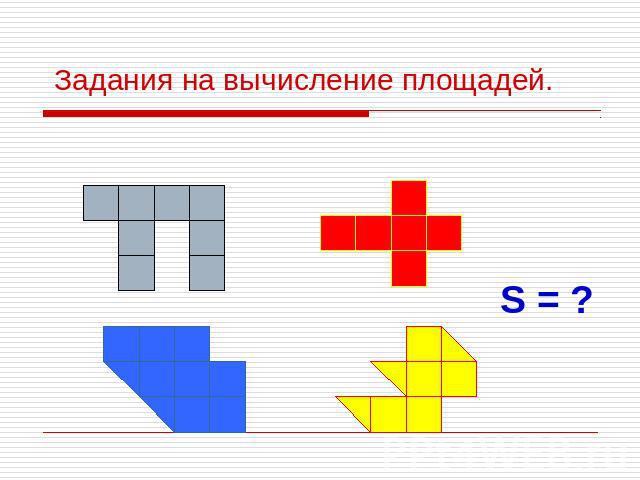
Задания на вычисление площадей.

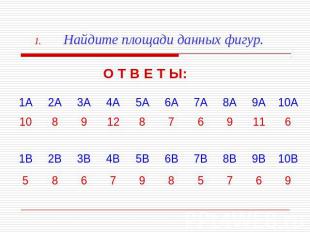
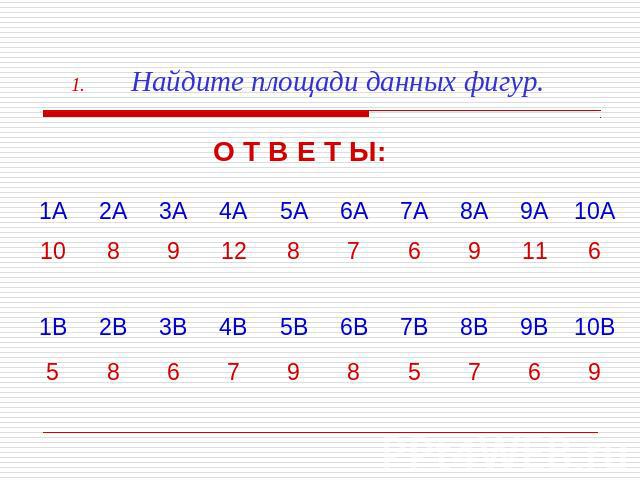
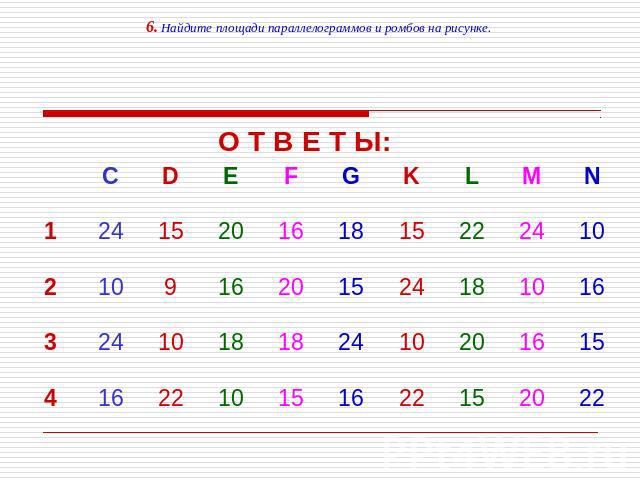
Найдите площади данных фигур. О Т В Е Т Ы:

2. Нарисуйте в тетради фигуры площадью:а) 2см2; б) 3см2; в) 5см2. ПОДСКАЗКА Не забудьте, что 1см равен двум клеткам тетради!

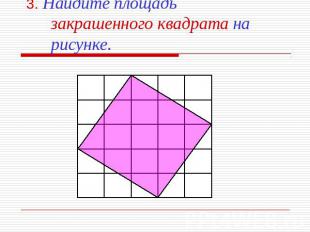
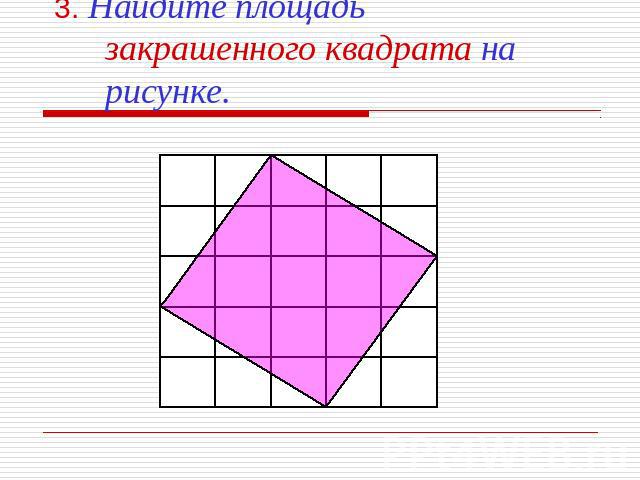
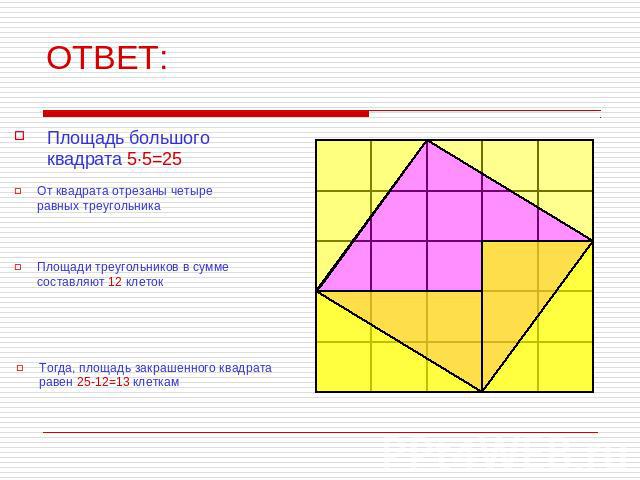
3. Найдите площадь закрашенного квадрата на рисунке.

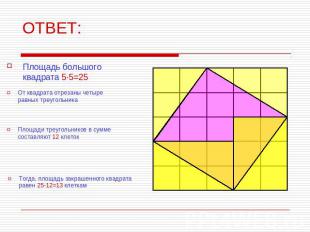
ОТВЕТ: Площадь большого квадрата 5·5=25 От квадрата отрезаны четыре равных треугольника Площади треугольников в сумме составляют 12 клеток Тогда, площадь закрашенного квадрата равен 25-12=13 клеткам

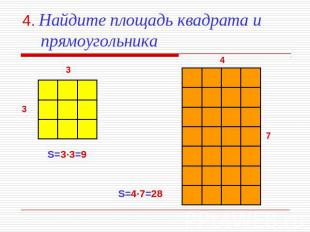
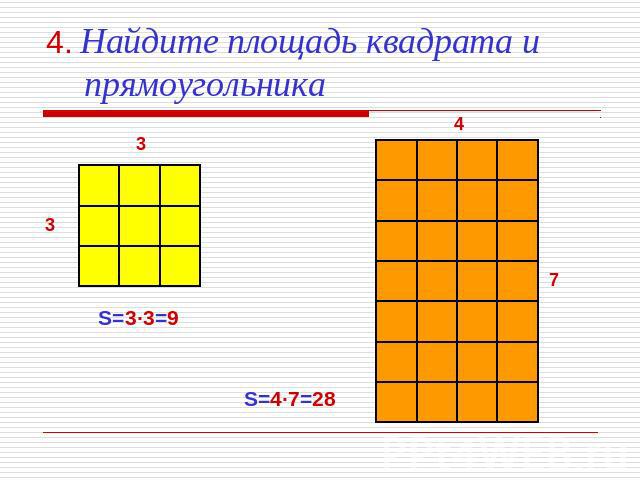
4. Найдите площадь квадрата и прямоугольника S=3·3=9 S=4·7=28

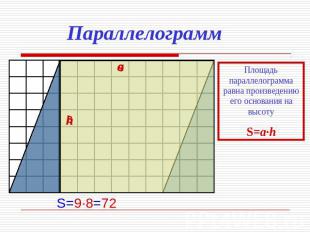
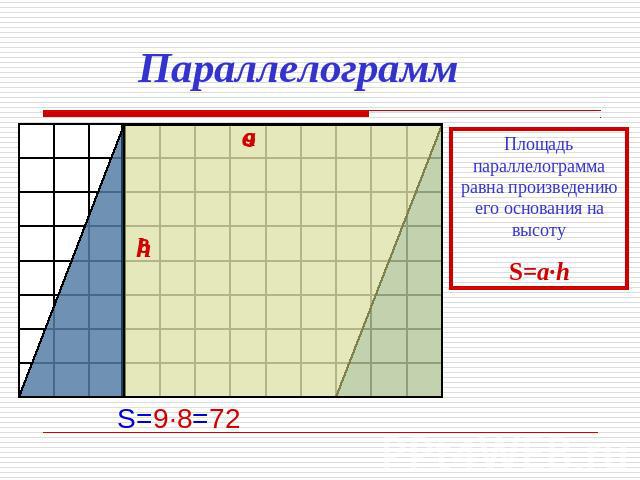
Параллелограмм Площадь параллелограмма равна произведению его основания на высоту S=a·h S=9·8=72

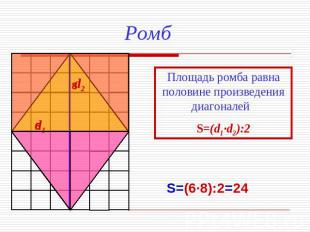
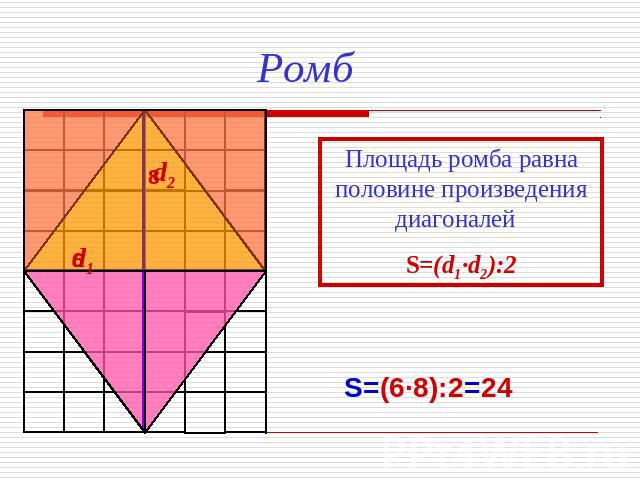
Ромб Площадь ромба равна половине произведения диагоналей S=(d1·d2):2 S=(6·8):2=24

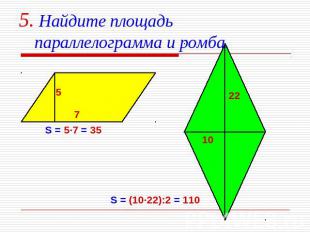
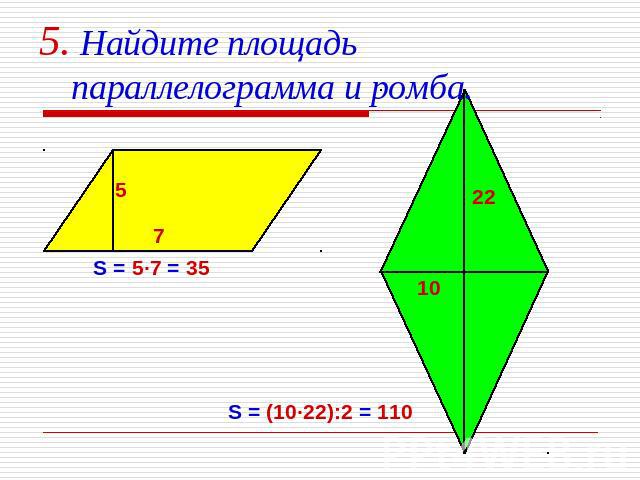
5. Найдите площадь параллелограмма и ромба. S = 5·7 = 35 S = (10·22):2 = 110

6. Найдите площади параллелограммов и ромбов на рисунке.

Оценочный лист Оценка «3»: 7 – 9 баллов; Оценка «4»: 10 – 13 баллов; Оценка «5»: 14 – 15 баллов.