Презентация на тему: Нахождение угла между скрещивающимися прямыми

Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №85 г.о. ТольяттиНахождение угла между скрещивающимися прямыми. Решение задач уровня С.учитель математики высшей категории Баленко Тамара Борисовна

Нахождение угла между скрещивающимися прямымиДанная тема актуальна, так как подобные задачи требуют развитого абстрактного мышления. Задачи, представленные ниже, чаще всего вызывают затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач.

Аргументы.1). Определение скрещивающихся прямых.2). Определение угла между скрещивающимися прямыми.3). Признак скрещивающихся прямых.4). Теорема Пифагора.5). Свойство высоты равнобедренного треугольника, проведенной к основанию.6). Определение правильной призмы.7). Определение синуса острого угла прямоугольного треугольника.8). Определение косинуса острого угла прямоугольного треугольника.9). Определение правильного многоугольника.10). Теорема о сумме углов выпуклого многоугольника.11). Свойство окружности, описанной около правильного шестиугольника.

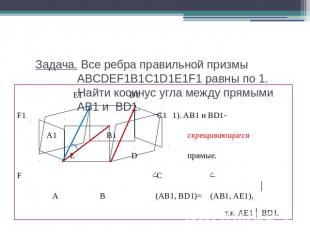
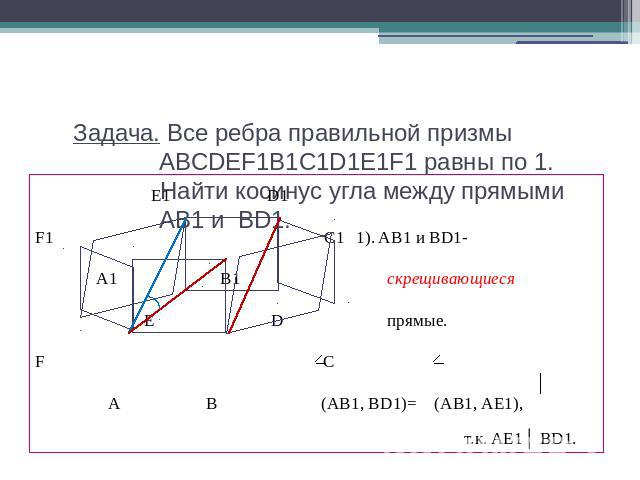
Задача. Все ребра правильной призмы ABCDEF1B1C1D1E1F1 равны по 1. Найти косинус угла между прямыми AB1 и BD1. E1 D1 F1 C1 1). AB1 и BD1- A1 B1 скрещивающиеся E D прямые.F C A B (AB1, BD1)= (AB1, AE1), т.к. AE1│ BD1.

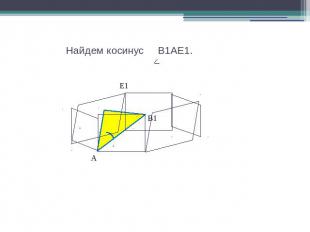
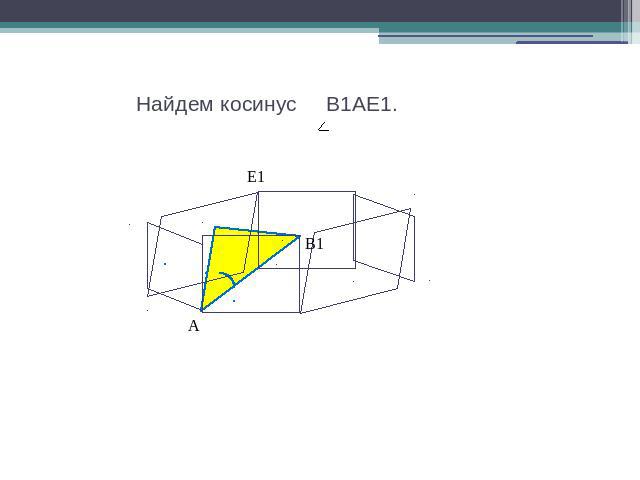
Найдем косинус B1AE1.

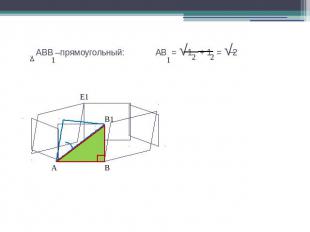
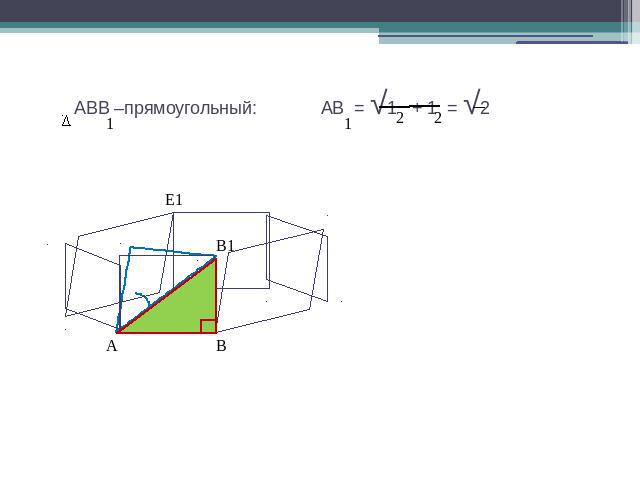
АВВ –прямоугольный: АВ = √1 + 1 = √2

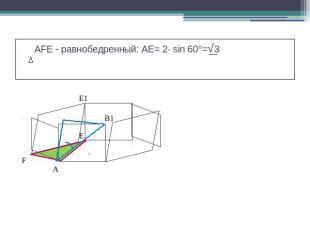
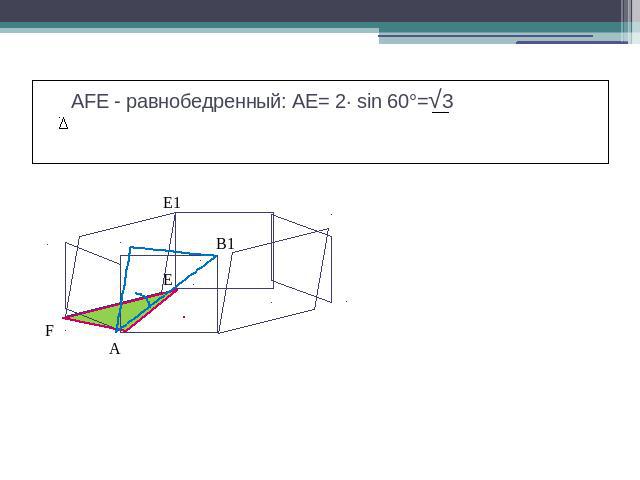
AFE - равнобедренный: АЕ= 2· sin 60°=√3

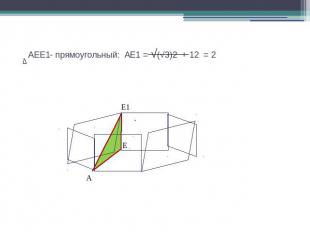
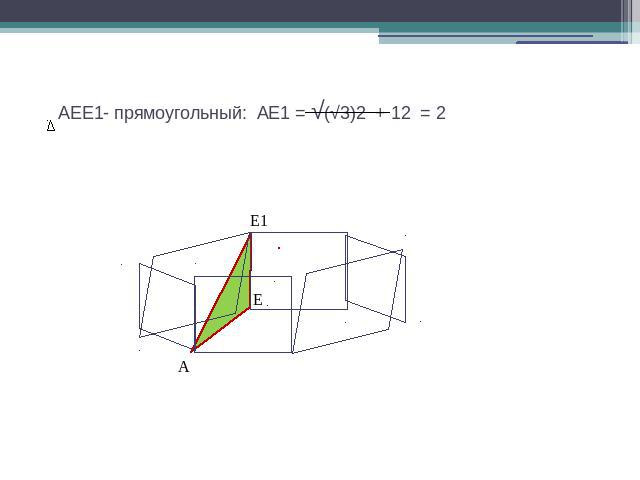
AEE1- прямоугольный: АЕ1 = √(√3)2 + 12 = 2

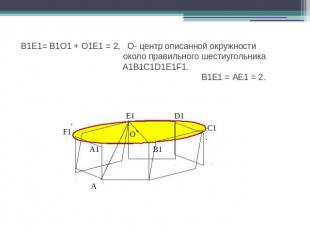
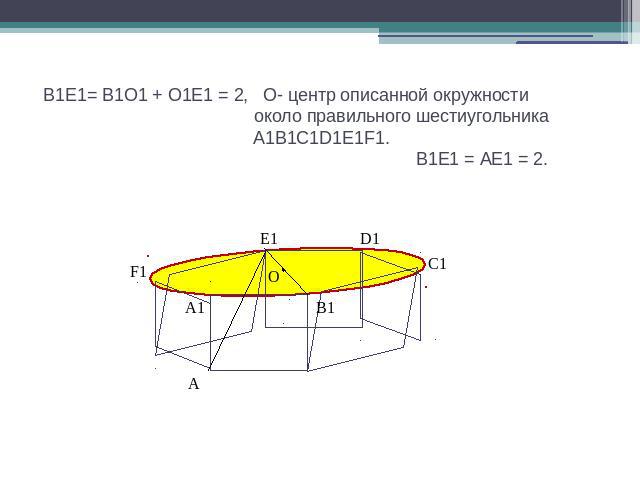
В1Е1= В1О1 + О1Е1 = 2, О- центр описанной окружности около правильного шестиугольника A1B1C1D1E1F1. В1Е1 = АЕ1 = 2.

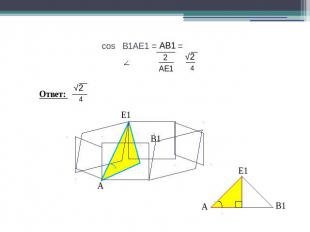
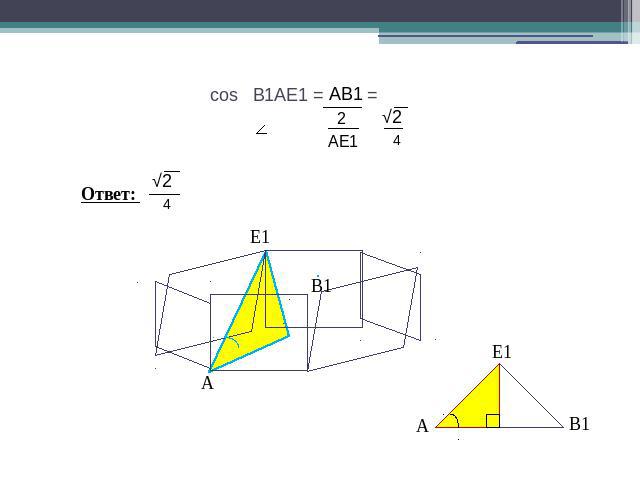
cos В1АЕ1 = =

Спасибо за внимание.