Презентация на тему: Параллелограмм

Параллелограмм

Какая фигура называется параллелограммом? Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых. ABCD – параллелограмм, AB║CD, BC║ AD

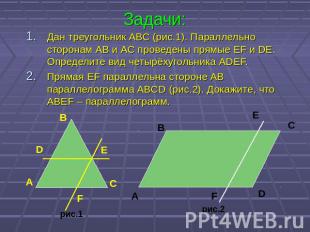
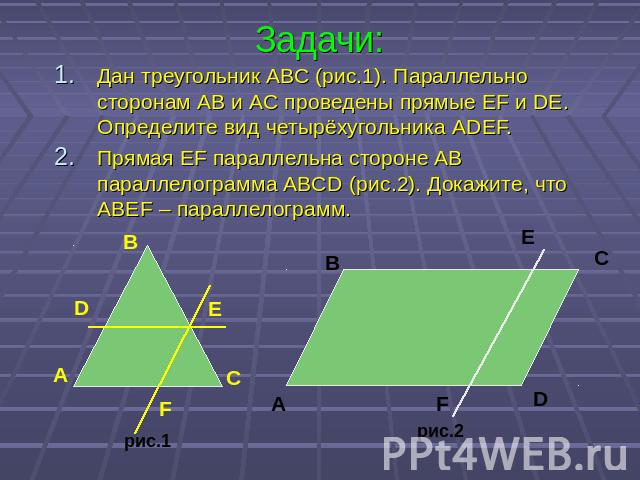
Задачи: Дан треугольник АВС (рис.1). Параллельно сторонам АВ и АС проведены прямые EF и DE. Определите вид четырёхугольника ADEF. Прямая EF параллельна стороне AB параллелограмма ABCD (рис.2). Докажите, что ABEF – параллелограмм.

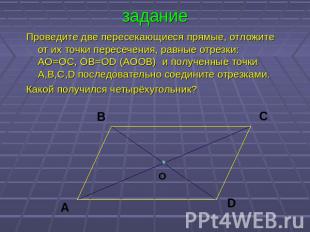
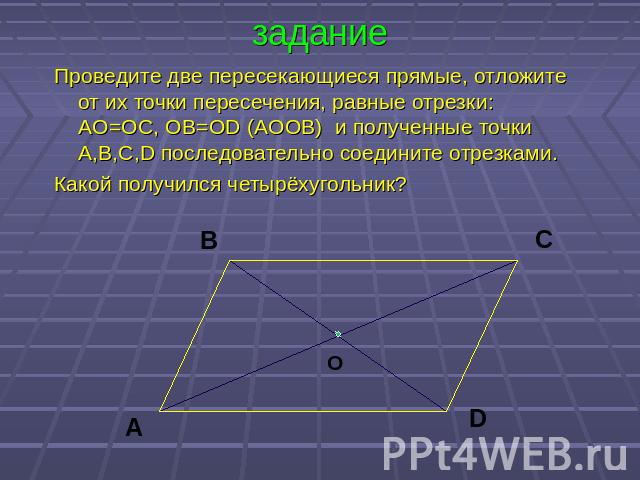
задание Проведите две пересекающиеся прямые, отложите от их точки пересечения, равные отрезки: AO=OC, OB=OD (AOOB) и полученные точки A,B,C,D последовательно соедините отрезками. Какой получился четырёхугольник?

Теорема (признак параллелограмма): Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. Дано: ABCD – четырёхугольник AC ∩ BD=O, AO=OC, OB=OD. Доказать: ABCD – параллелограмм. Доказательство. ∆ AOD = ∆ COB. У них AOD = COB – как вертикальные, OD=OB и OA=OC – по условию. Значит OBC = ODA, а они внутренние накрест лежащие, для прямых AD и BC, и секущей BD. По признаку параллельности прямых прямые AD и BC параллельны. Также доказывается параллельность прямых AB и CD с помощью равенства треугольников AOB и COD. Так как противолежащие стороны четырёхугольника параллельны, то по определению этот четырёхугольник – параллелограмм. Теорема доказана.

Задачи. Дано: четырёхугольник ABCD, AC= 6 см, BD=8 см, AO=3 см, OD=4 см. Определите вид четырёхугольника ABCD. 2) Дано: AO – медиана ∆ ABD, BO – медиана ∆ ABC. Докажите, что ABCD – параллелограмм.

Ответьте на вопросы Что такое параллелограмм? Сформулируйте теорему 6.1.(признак параллелограмма) Домашнее задание: п 51, №3,№4 стр. 79