Презентация на тему: Многоугольник

Многоугольник Геометрия, 9 класс Учитель Вишневская Н.В.

План урока Понятие ломаной. Длина ломаной Понятие многоугольника Выпуклые и невыпуклые многоуголь-ники Сумма углов многоугольника Правильные многоугольники

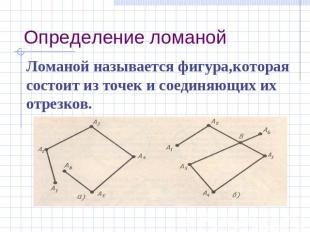
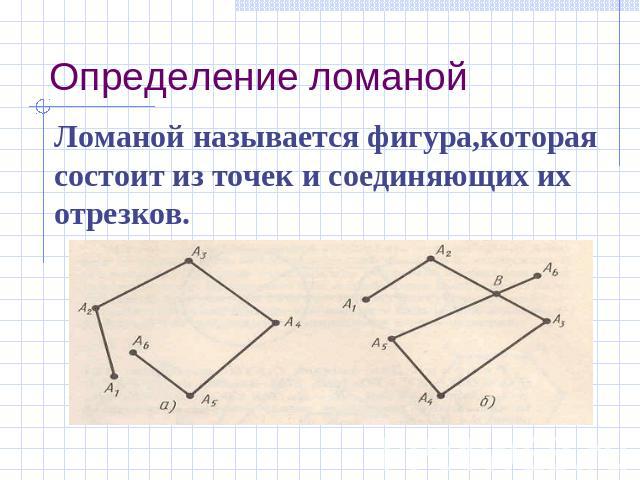
Определение ломаной Ломаной называется фигура,которая состоит из точек и соединяющих их отрезков.

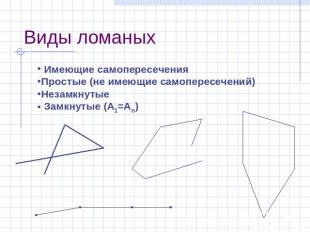
Виды ломаных Имеющие самопересечения Простые (не имеющие самопересечений) Незамкнутые Замкнутые (А1=Аn)

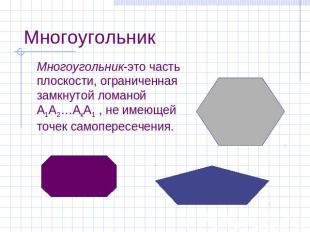
Многоугольник Многоугольник-это часть плоскости, ограниченная замкнутой ломаной А1А2…АкА1 , не имеющей точек самопересечения.

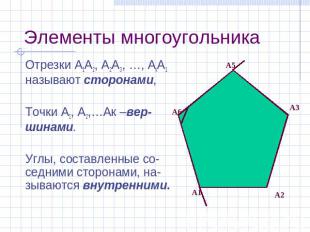
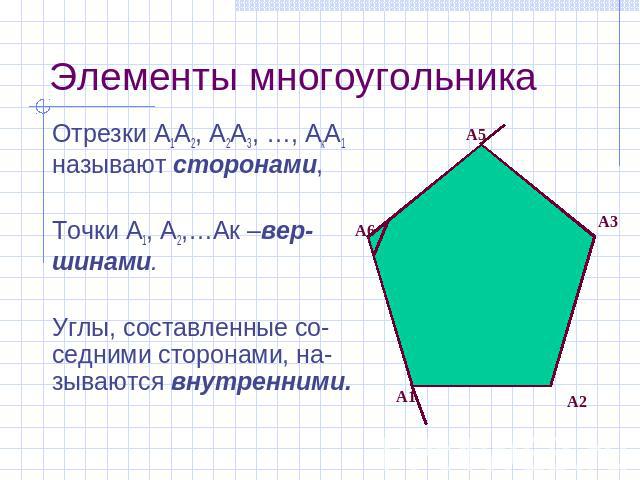
Элементы многоугольника Отрезки А1А2, А2А3, …, АкА1 называют сторонами, Точки А1, А2,…Ак –вер-шинами. Углы, составленные со-седними сторонами, на-зываются внутренними.

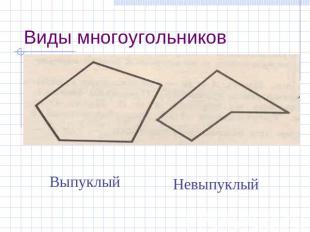
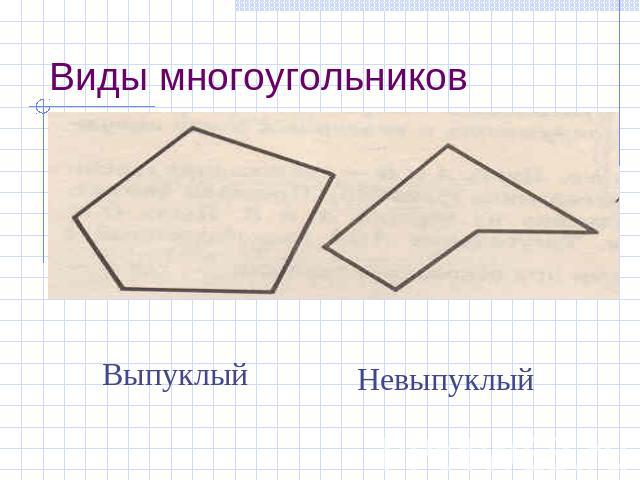
Виды многоугольников Выпуклый Невыпуклый

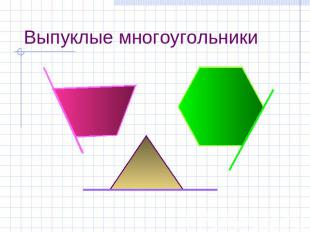
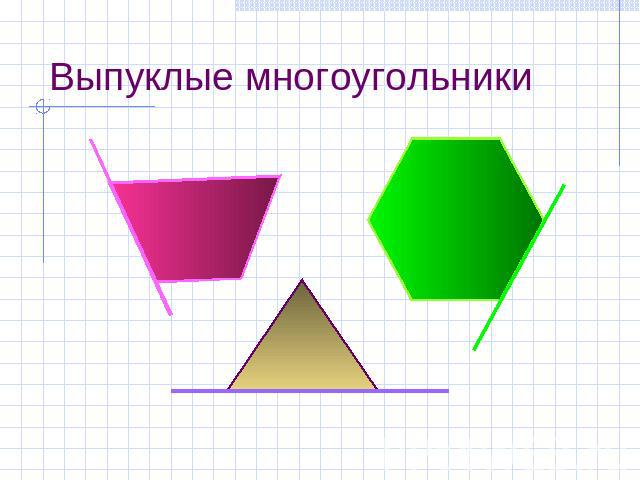
Выпуклые многоугольники

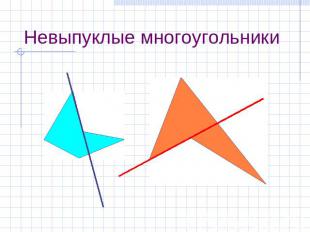
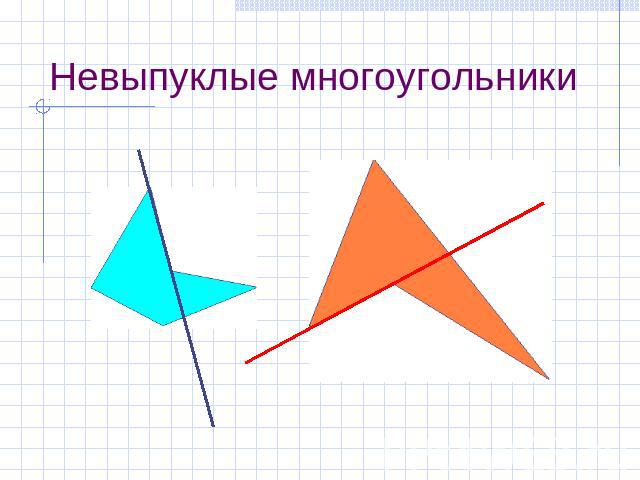
Невыпуклые многоугольники

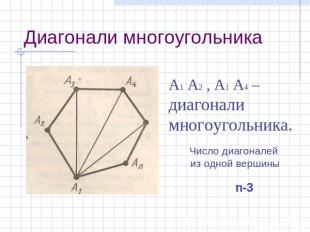
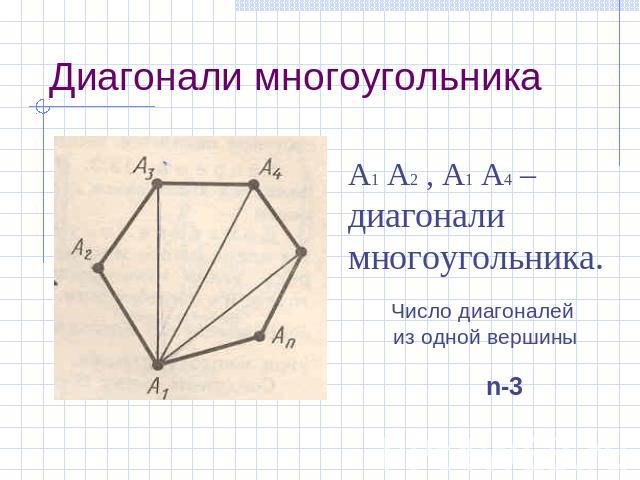
Диагонали многоугольника А1 А2 , А1 А4 – диагонали многоугольника. Число диагоналей из одной вершины n-3

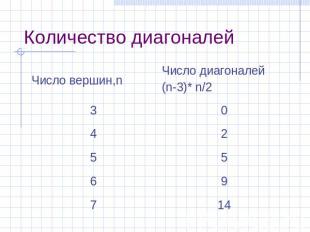
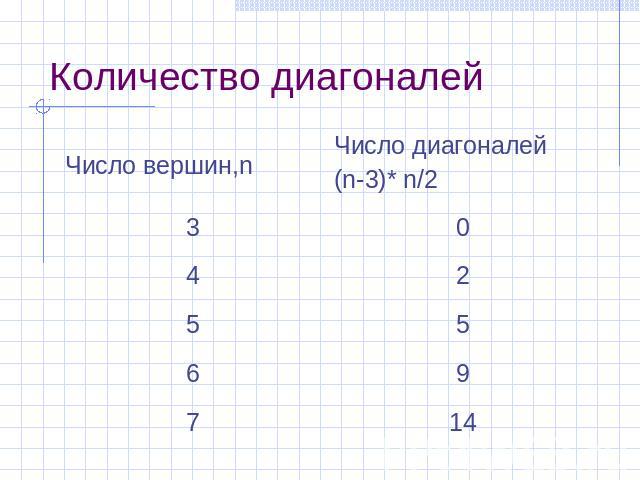
Количество диагоналей

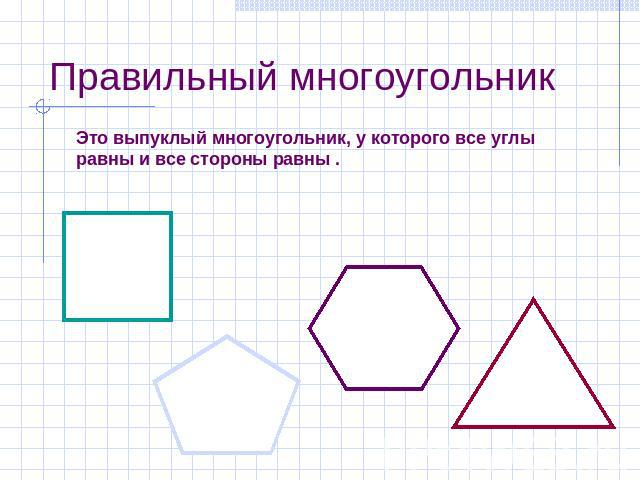
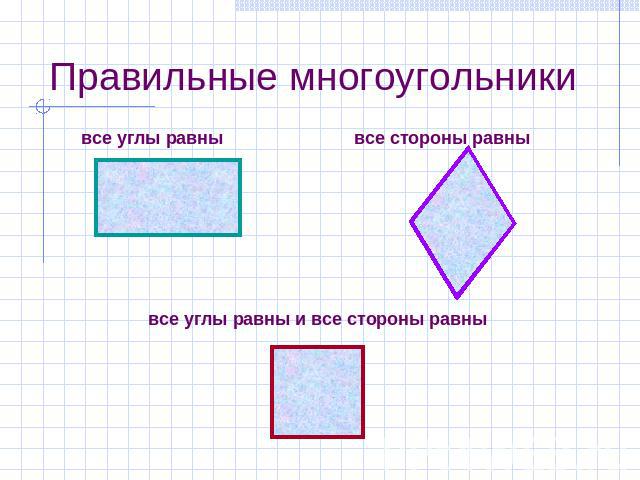
Правильный многоугольник Это выпуклый многоугольник, у которого все углы равны и все стороны равны .

Правильные многоугольники все углы равны все стороны равны все углы равны и все стороны равны

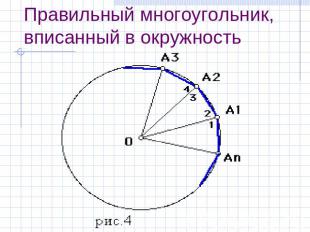
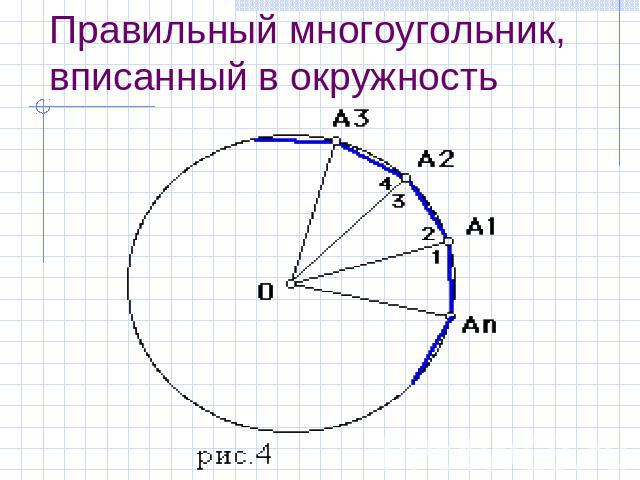
Правильный многоугольник, вписанный в окружность

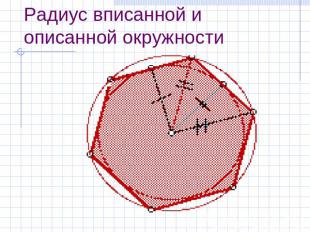
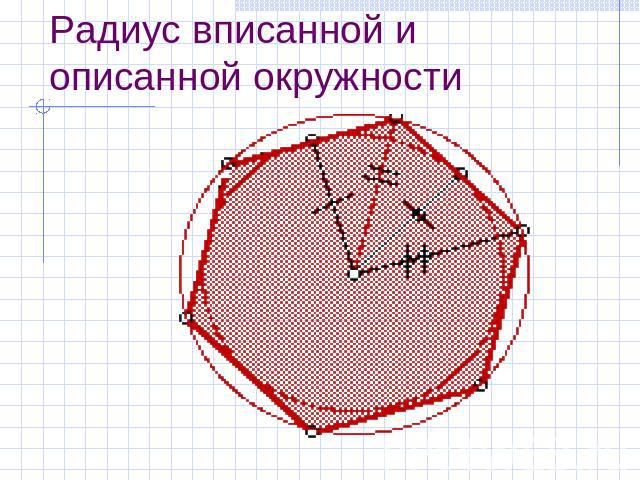
Радиус вписанной и описанной окружности

Паркеты из правильных многоугольников В математике паркетом называют «замощение» плоскости повторяю-щимися фигурами без пропусков и перекры-тий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников (3600: 600 = 6), либо четыре квадрата (3600: 900 = 4), либо три правильных шестиугольника (3600: 1200 = 3), так как сумма углов с вершиной этой точки равна 3600.

Правильные многоугольники в природе Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника? Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек. Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов. И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».

Творческие работы Правильные многоугольники в орнаментах и паркетах Правильные многоугольники в природе Кроссворд по теме