Презентация на тему: Линейные функции

ЛИНЕЙНЫе ФУНКЦИи

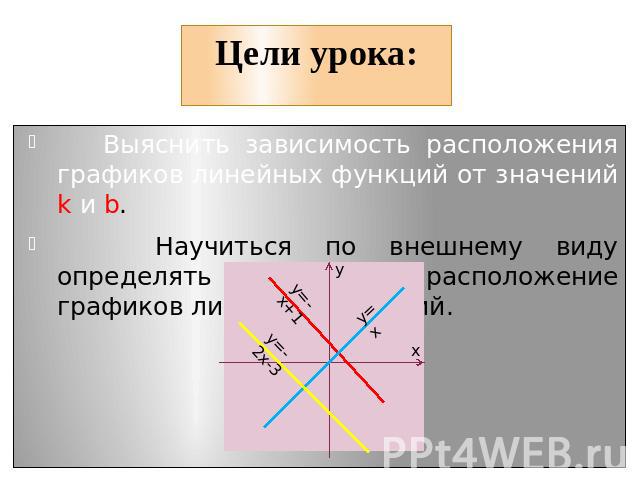
Цели урока: Выяснить зависимость расположения графиков линейных функций от значений k и b. Научиться по внешнему виду определять взаимное расположение графиков линейных функций.

АКТУАЛИЗАЦИЯ ЗНАНИЙ Какую функцию называют линейной? Что является графиком линейной функции? Сколько нужно отметить точек на плоскости , чтобы построить прямую? Как построить график линейной функции? Какую функцию называют прямой пропорциональностью? Что является графиком прямой пропорциональности? В каких координатных четвертях расположен график функции y=k •x при k>0‚k<0? Как называется k? Что зависит на графике от k? Каким может быть взаимное расположение двух прямых на плоскости?

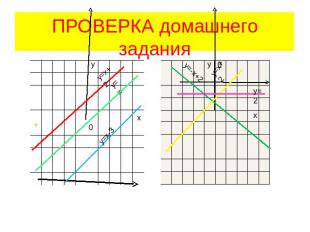
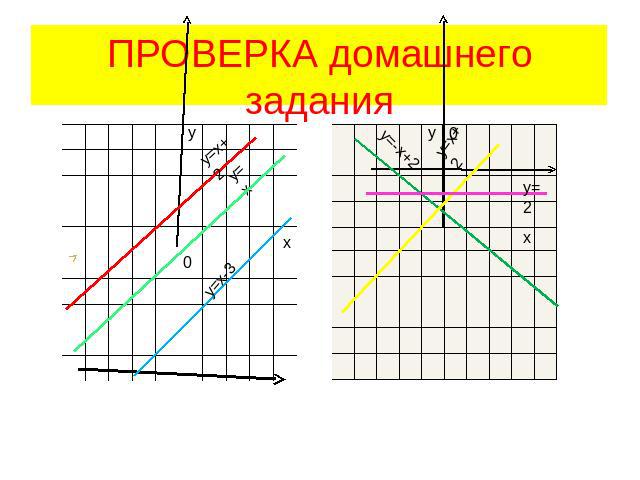
ПРОВЕРКА домашнего задания

Найти координаты точки пересечения графиков линейных функций у=-4х-1 и у=2х+5 4х-1=2х+5 4х-2х=5+1 2х=6 х=3 у=2·3=6 Ответ: (3, 2)

k>0 угол наклона прямой к оси ОХ острый;k<0 угол наклона прямой к оси ОХ тупой;k=0 прямая параллельна оси Ох b>0 график пересекает ось Оу выше оси Ох; b<0 график пересекает ось Оу ниже оси Ох; b=0 график проходит через начало координат (прямая пропорциональность) Даны : у=к₁х+в₁ и у=к₂х+в₂ Если: к₁≠к₂ графики пересекаются к₁≠к₂, в₁=в₂ графики пересекаются в точке(0,в) к₁=к₂, в₁≠в₂ графики параллельны к₁=к₂, в₁=в₂ графики совпадают

Среди функций, заданных формулами у=х+0,5 (1) ; у=-0,5х+4 (2) ; у=5х-1 (3) ; у=1+0,5х (4) ; у=2х-5 (5); у=0,5х-2 (6) назовите те, графики которых а)параллельны графику функции у=0,5х+4 б)пересекается с графиком функции у=2х+3 в)совпадает с графиком функции у=4-0,5х

Для функции у=35х-42 составить функцию, график которой: а)параллелен ему; б)параллелен ему и проходит через начало координат; в)пересекается с ним; г)пересекается с ним в точке (0,-42)

Задания: 1.Найти координаты точки пересечения графика у=3х+4 с осями координат; 2.График функции у=kх+5 проходит через точку М(-7,12).Найдите k. 3.График функции у=kх+b проходит через точку А(-3,2) и параллелен прямой у=-4х.Найдите к и в. Напишите получившуюся формулу.

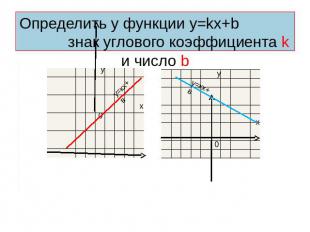
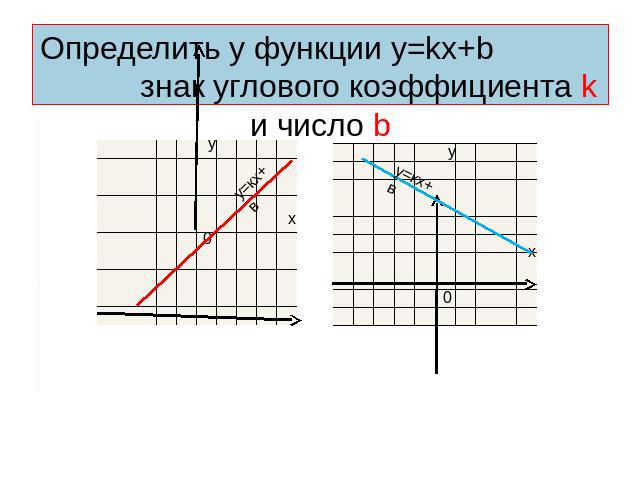
Определить у функции у=kх+b знак углового коэффициента k и число b

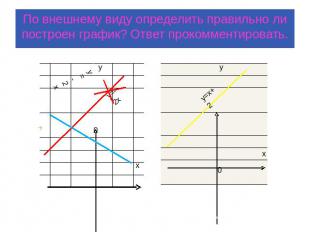
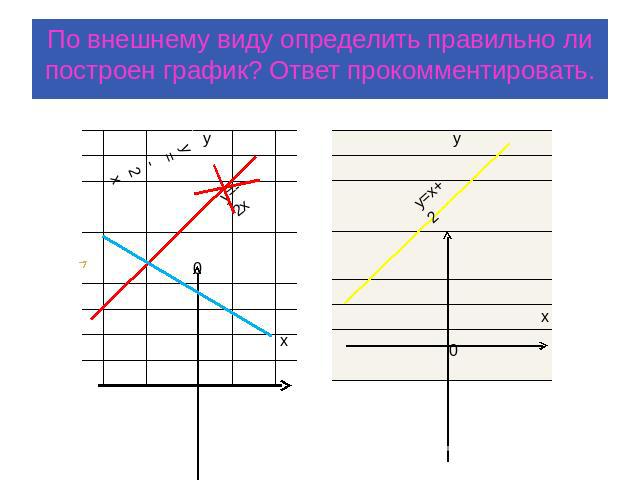
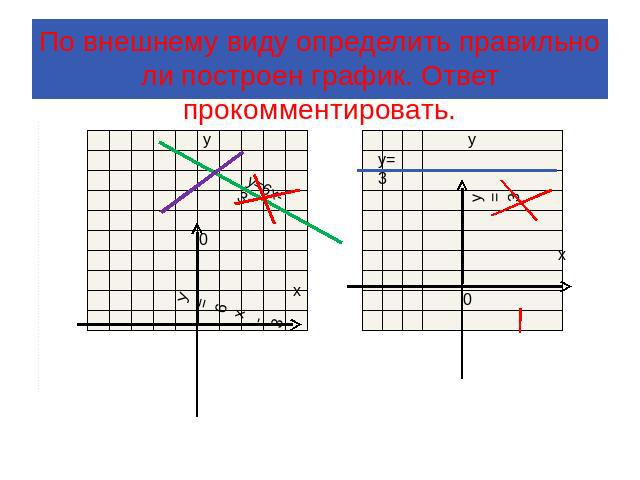
По внешнему виду определить правильно ли построен график? Ответ прокомментировать.

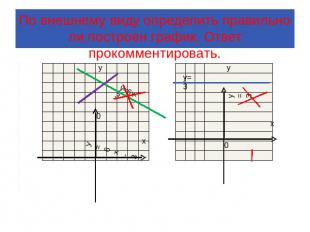
По внешнему виду определить правильно ли построен график. Ответ прокомментировать.

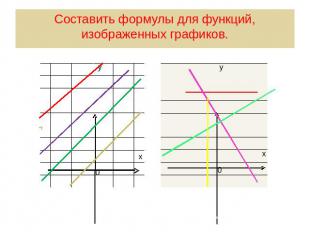
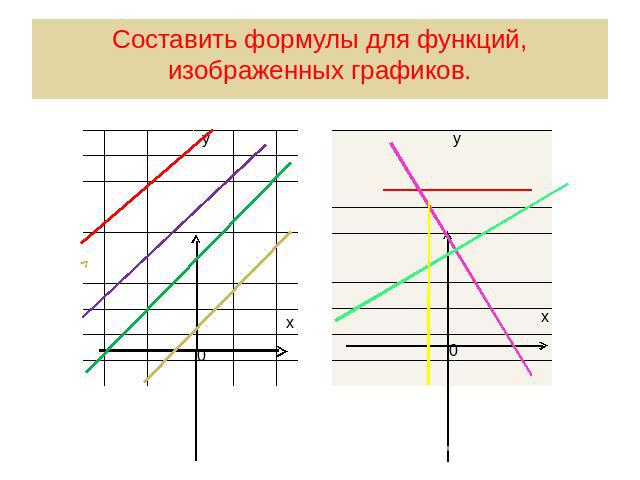
Составить формулы для функций, изображенных графиков.