Презентация на тему: Теорема Пифагора

Теорема Пифагора

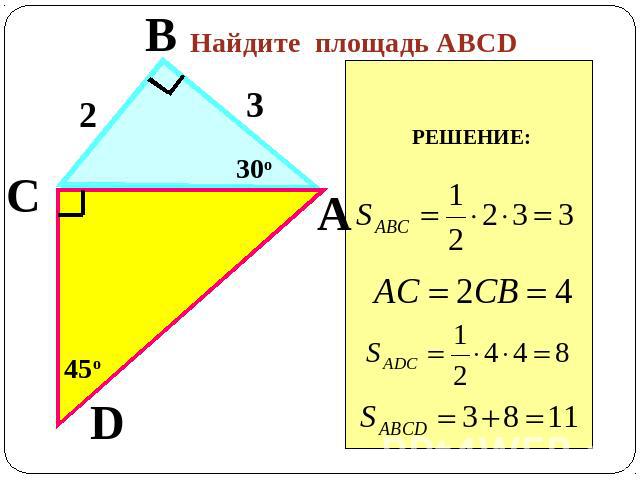
Устная работа

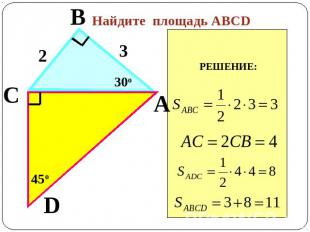
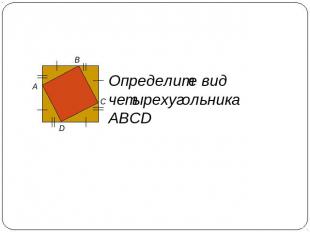
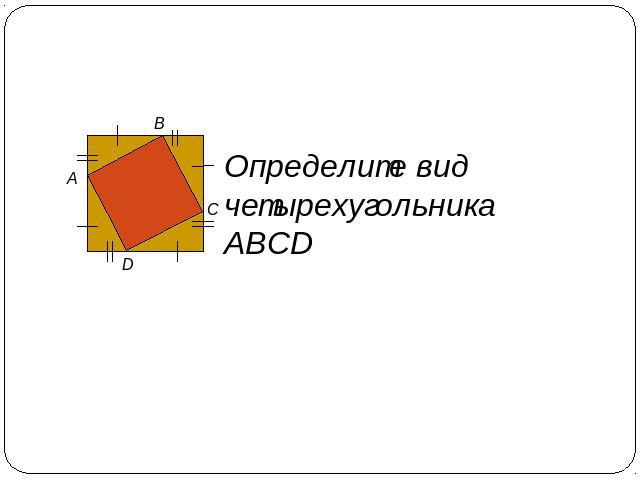
Определите вид четырехугольника АВСD

Теорема Пифагора Из истории Теорема Пифагора

Рафаэль. Пифагор в окружении учеников.

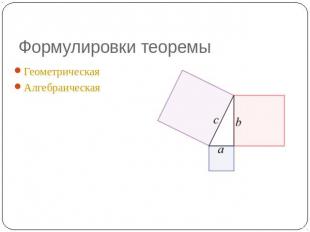
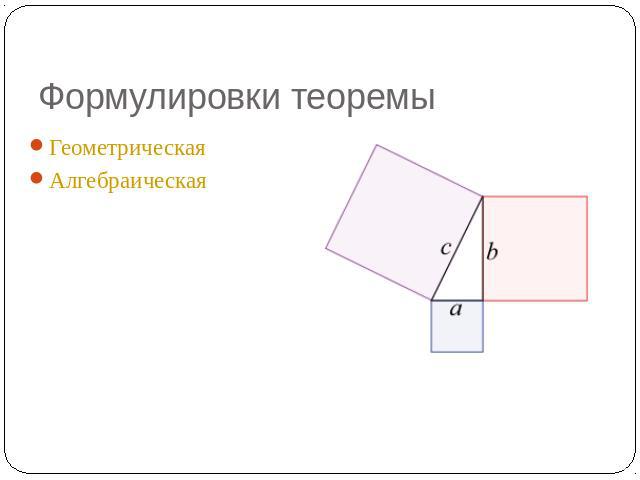
Формулировки теоремы Геометрическая Алгебраическая

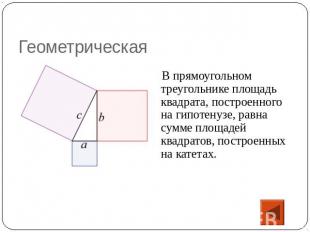
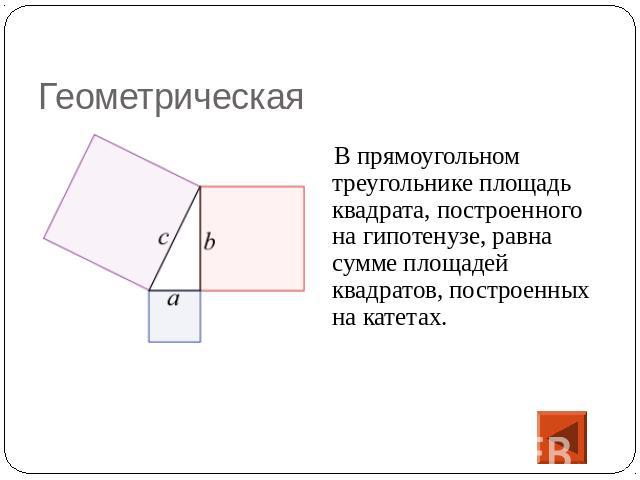
Геометрическая В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

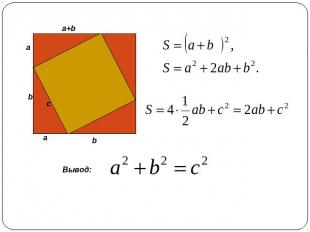
Алгебраическая В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:

Доказательства В научной литературе зафиксировано 367 доказательств данной теоремы. Теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Способы доказательства теоремы: Через подобные треугольники. Доказательство методом площадей. Доказательство через равнодополняемость. Доказательство через равносоставленность. Доказательство Евклида.

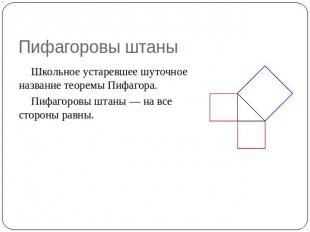
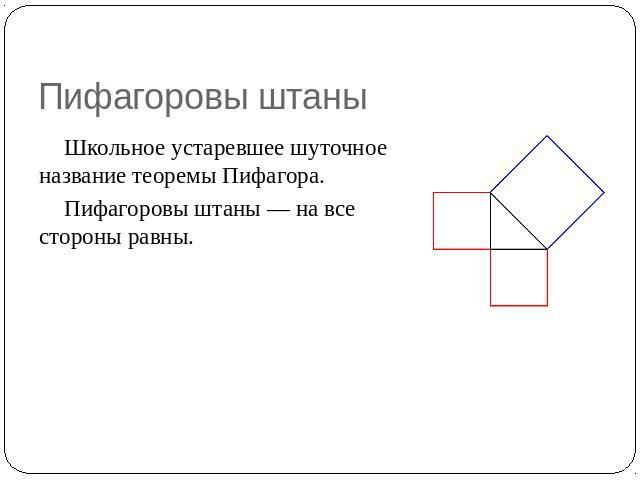
Пифагоровы штаны Школьное устаревшее шуточное название теоремы Пифагора. Пифагоровы штаны — на все стороны равны.

И .Дырченко Если дан нам треугольник, И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим- И таким простым путем К результату мы придем.

Самое ценное в математике - это возможность быстрого приложения теории к практике

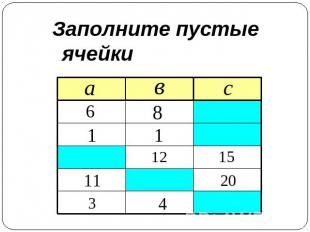
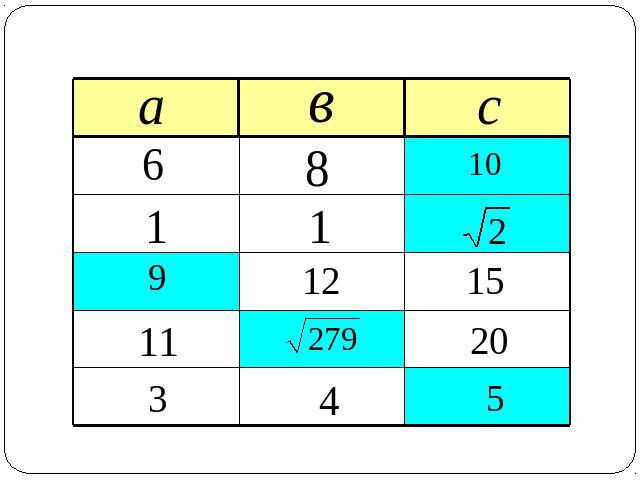
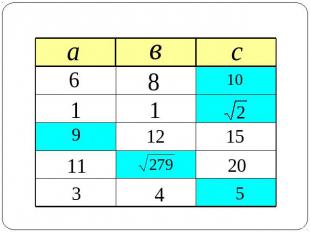
Заполните пустые ячейки таблицы

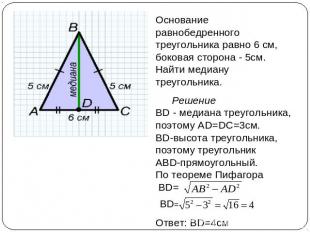
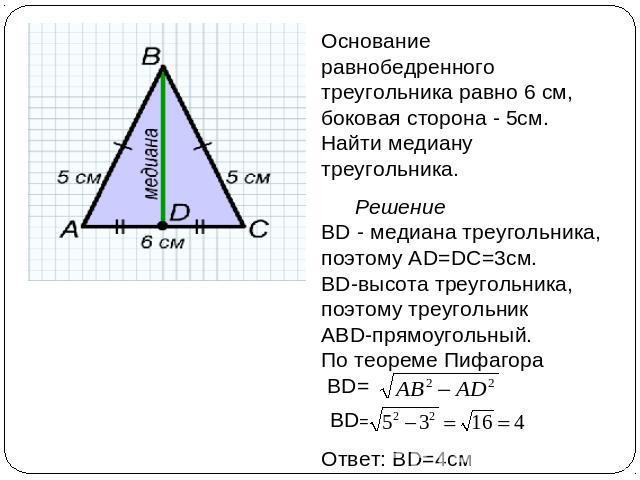
Основание равнобедренного треугольника равно 6 см, боковая сторона - 5см. Найти медиану треугольника. Решение ВD - медиана треугольника, поэтому АD=DC=3см. BD-высота треугольника, поэтому треугольник АВD-прямоугольный. По теореме Пифагора ВD=

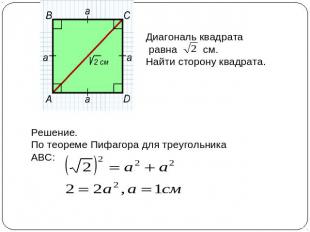
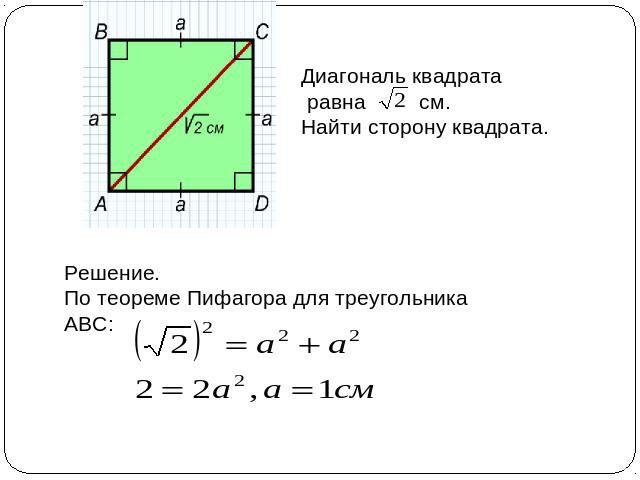
Диагональ квадрата равна см. Найти сторону квадрата. Решение. По теореме Пифагора для треугольника АВС:

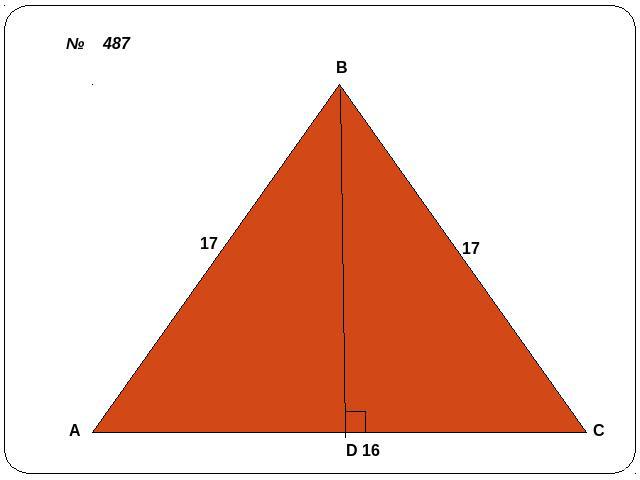
Дано: АВС-равнобедренный АВ=17см, АС=16 см, ВD АС. Найти: ВD