Презентация на тему: Признаки равенства треугольников

Признаки равенства треугольников Урок в 7 классе Г Учитель Мошнина Ирина Владимировна

Треугольник Треугольник - простейшая плоская фигура. Три вершины и три стороны. Изучение треугольника породило науку – тригонометрию. Эта наука возникла из практических потребностей при измерении земельных участков, составлении карт на местности, конструировании машин и механизмов.

Первое упоминание о треугольнике и его свойствах мы находим в египетских папирусах Которым более 4000лет.Через 2000лет в древней Греции

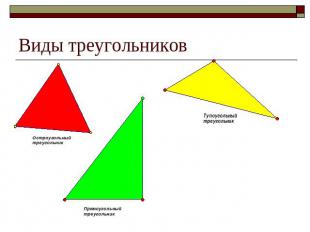
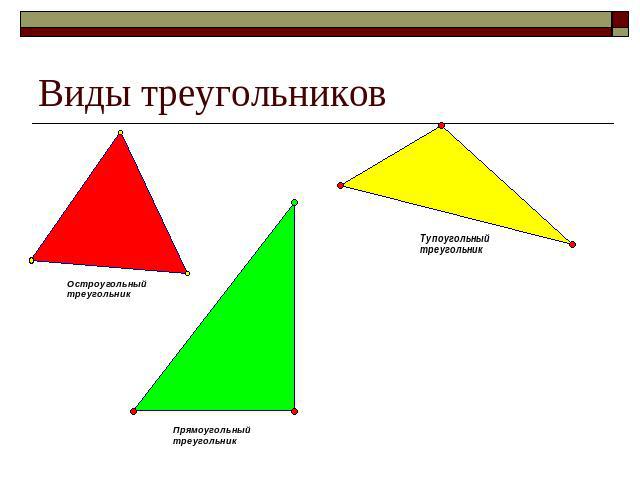
Виды треугольников

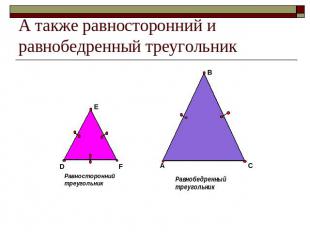
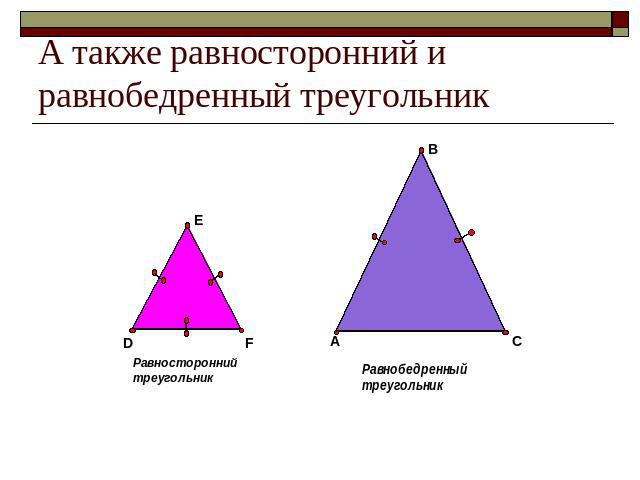
А также равносторонний и равнобедренный треугольник

Медиана треугольника Отрезок соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Любой треугольник имеет три медианы

Высота треугольника Перпендикуляр проведенный из вершины треугольника к прямой, содержащей противоположную. Сторону, называется высотой треугольника Любой треугольник имеет три высоты

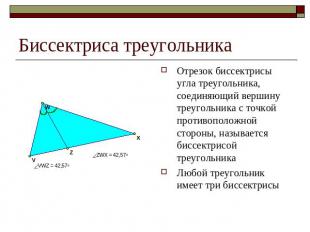
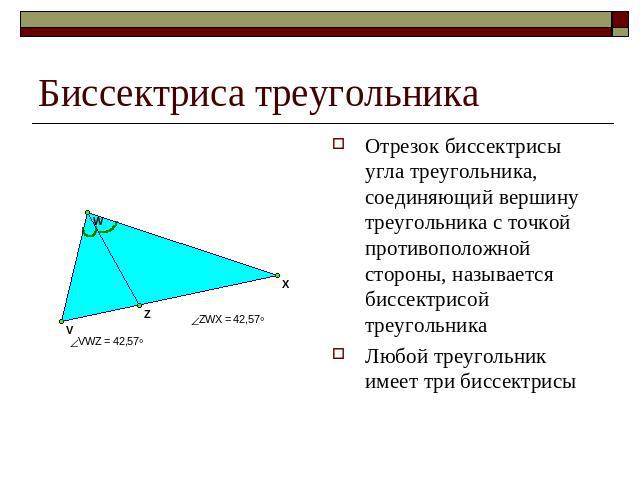
Биссектриса треугольника Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника Любой треугольник имеет три биссектрисы

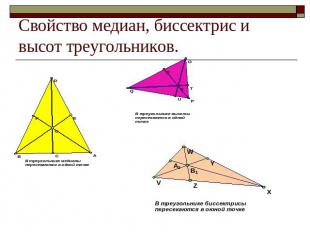
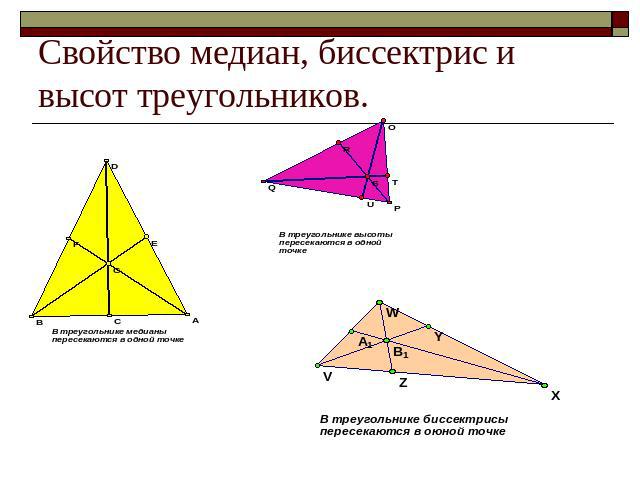
Свойство медиан, биссектрис и высот треугольников.

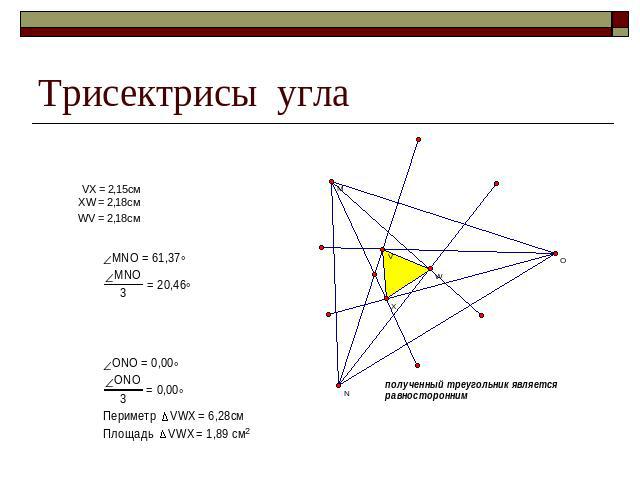
Открытия в геометрии треугольника есть и в нашем веке Так, в 1904 году американский математик Ф.Морли доказал , что если из каждой вершины треугольника провести лучи, делящие соответствующий угол на три равные части(трисектрисы угла,) то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника. Доказательство этого утверждения было под силу и древнегреческим математикам , но они прошли мимо этого факта, видимо, потому, что тогда было принято рассматривать лишь построения при помощи циркуля и линейки, а с помощью этих инструментов такое деление сделать не возможно.

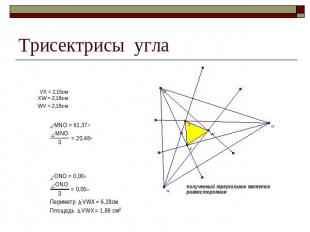
Трисектрисы угла

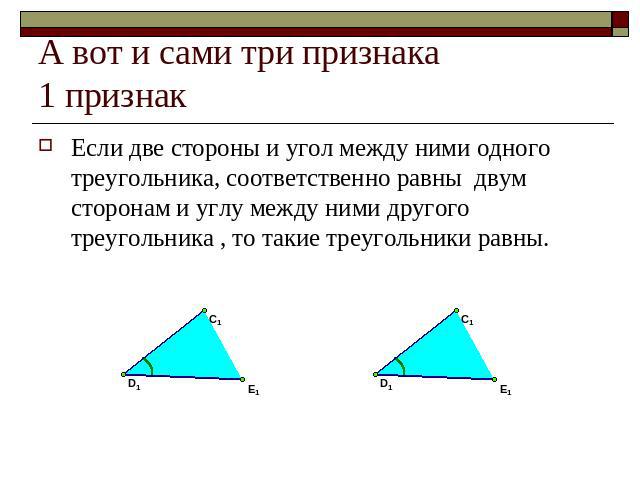
А вот и сами три признака1 признак Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника , то такие треугольники равны.

2-й признак Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника , то такие треугольники равны.

3-й признак Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника . То такие треугольники равны.

Решение задач Желаем удачи! 06.12.06 Признаки