Презентация на тему: Признаки равенства треугольников

Признаки равенства треугольников Треугольник и его элементыЗадачи по теме «Первый признак равенства треугольников»Задачи по теме «Второй признак равенства треугольников»Задачи по теме «Третий признак равенства треугольников»Справочный материал (формулировка теоремы и ее доказательство): а) Первый признак равенства треугольников б) Второй признак равенства треугольников в) Третий признак равенства треугольников

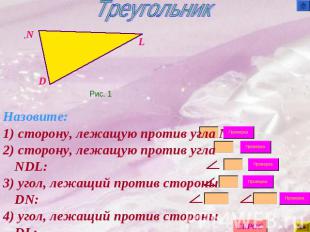
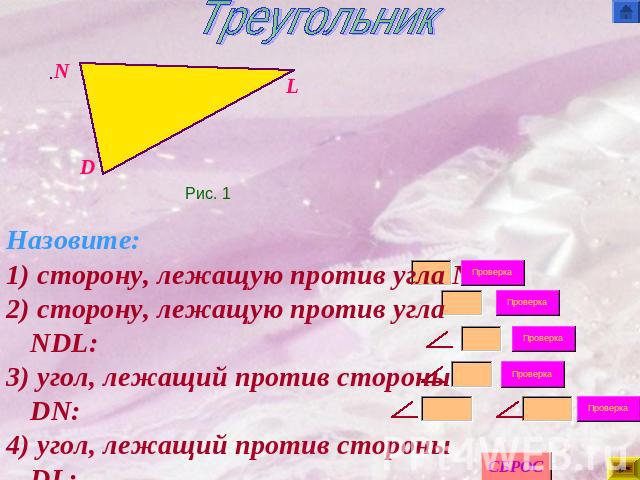
Треугольник Назовите:1) сторону, лежащую против угла N :2) сторону, лежащую против угла NDL:3) угол, лежащий против стороны DN:4) угол, лежащий против стороны DL:5) углы, прилежащие к стороне NL: и

Первый признак равенства треугольников Задача. Заполните пропуски. Докажите, что OLF = OMNРешение:1) Рассмотрим OLF и :а) OL = - по условию,б) OF = - по условию, в) LOF = - как вертикальные углы. Следовательно OLF = - по двум сторонам и углу между ними.

Задача. Заполните пропуски. Докажите, что ARS = BRS а) Сторона = - по условию.б) Сторона = - общая сторона.в) = - по условию.г) Следовательно, ARS = - по двум и углу .2) Т. к. ASR= BSR, то соответственные стороны и углы равны, BR = AR = 18 см, BRS = ARS =

Второй признак равенства треугольников Докажите, что AXO = BZOРешение: У них: а) Сторона = - по условию; б) = - по условию; в) = - как вертикальные.Следовательно AXO = - по стороне и двум прилежащим к ней .

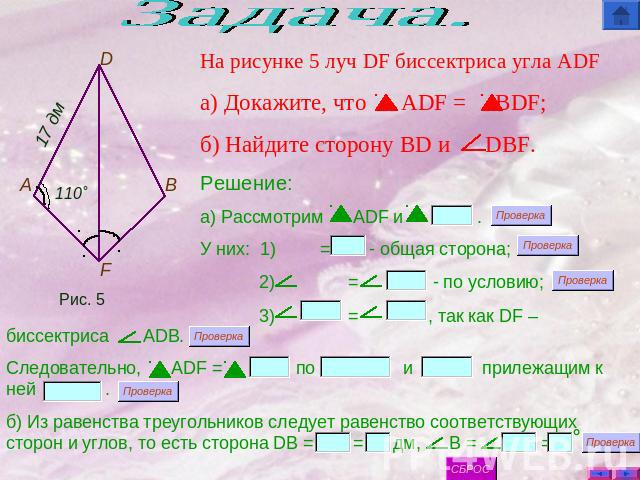
Задача. На рисунке 5 луч DF биссектриса угла ADFа) Докажите, что ADF = BDF;б) Найдите сторону BD и DBF.Решение: а) Рассмотрим ADF и .У них: 1) = - общая сторона; 2) = - по условию; 3) = , так как DF – биссектриса ADB.Следовательно, ADF = по и прилежащим к ней .б) Из равенства треугольников следует равенство соответствующих сторон и углов, то есть сторона DB = = дм, B = = .

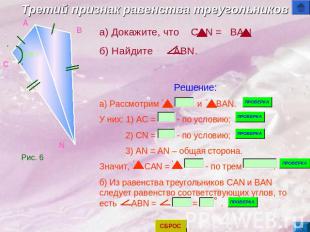
Третий признак равенства треугольников а) Докажите, что CAN = BANб) Найдите ABN.Решение:а) Рассмотрим и BAN. У них: 1) AC = - по условию; 2) CN = - по условию; 3) AN = AN – общая сторона.Значит, CAN = - по трем . б) Из равенства треугольников CAN и BAN следует равенство соответствующих углов, то есть ABN = = .

Теорема Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Рассмотрим треугольники ABC и DEF, у которых AB=DE, AC=DF, углы A и D равны (рис. 7). Докажем, что ABC = DEF.Так как A = D, то треугольник ABC можно наложить на треугольник DEF так, что вершина A совместится с вершиной D, а стороны AB и AC наложатся соответственно на лучи DE и DF. Поскольку AB=DE, AC=DF, то сторона AB совместится со стороной DE, а сторона AC – со стороной DF; в частности, совместятся точки B и E, C и F. Следовательно, совместятся стороны BC и EF. Итак, треугольники ABC и DEF полностью совместятся, значит, они равны.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Доказательство Рассмотрим треугольники ABC и DEF, у которых AB = DE, A = D, B = E (рис. 8). Докажем, что ABC= DEF.Наложим треугольник ABC на треугольник DEF так, чтобы вершина A совместилась с вершиной D, сторона AB – с равной ей стороной DE, а вершины C и F оказались по одну сторону от прямой DE.Так как A = D и B= E, то сторона AC наложится на луч DF, а сторона BC – на луч EF. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче DF, так и на луче EF и, следовательно, совместится с общей точкой этих лучей – вершиной F. Значит, совместятся стороны AC и DF, BC и EF. Итак, треугольники ABC и DEF полностью совместятся, поэтому они равны.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Рассмотрим треугольники ABC и DEF, у которых AB = DE, BC = EF, CA = FD (рис. 9). Докажем, что ABC = DEF. Приложим треугольник ABC к треугольнику DEF так, чтобы вершина A совместилась с вершиной D, вершина B – с вершиной E, а вершины C и F оказались по разные стороны от прямой DE (рис. 10).Возможны три случая: луч FC проходит внутри угла DFE (рис. 10, а); луч FC совпадает с одной из сторон этого угла (рис. 10, б); луч FC проходит вне угла DFE (рис. 10, в). Рассмотрим первый случай (остальные случаи можете рассмотреть самостоятельно). Так как по условию теоремы стороны AC и DF, BC и EF равны, то треугольники DFC и EFC – равнобедренные (см. рис. 10, а). По теореме о свойстве углов равнобедренного треугольника 1 = 2, 3 = 4, поэтому DCE = DFE. Итак, AC = DF, BC = EF, C = F.Следовательно, треугольники ABC и DEF равны по первому признаку равенства треугольников.