Презентация на тему: Теорема Пифагора

Урок по теме«Теорема Пифагора» c² = a² + b²

Исторический экскурсРассказ о Пифагоре Пифагор жил в VI в. до н. э. в Древней Греции Основал философскую школу – пифагорейский союз.

Пифагорейцы занимались математикой, философией, естественными науками. Ими были сделаны важные открытия в арифметике и геометрии. В школе существовало правило, по которому авторство всех работ приписывалось Пифагору. Так что достоверно неизвестно, какие открытия принадлежат самому ученому.

Из истории теоремы Пифагора Во времена самого ученого её формулировали так: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».Или в виде задачи: « Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах: S = S1 + S2».

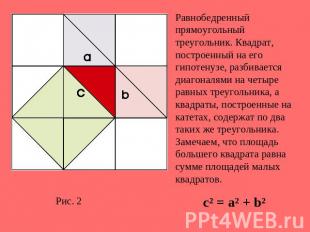
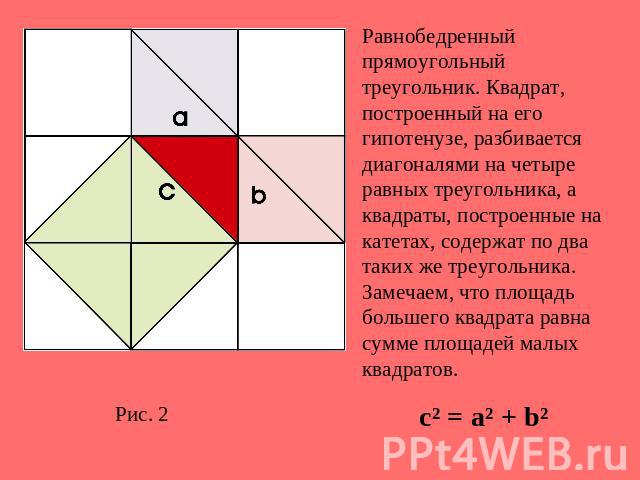
Равнобедренный прямоугольный треугольник. Квадрат, построенный на его гипотенузе, разбивается диагоналями на четыре равных треугольника, а квадраты, построенные на катетах, содержат по два таких же треугольника. Замечаем, что площадь большего квадрата равна сумме площадей малых квадратов.с² = a² + b²

Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его «ослиным мостом» или «бегством убогих»

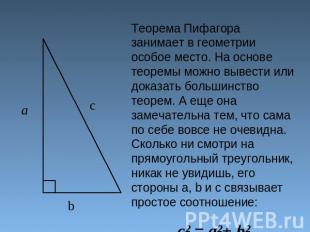
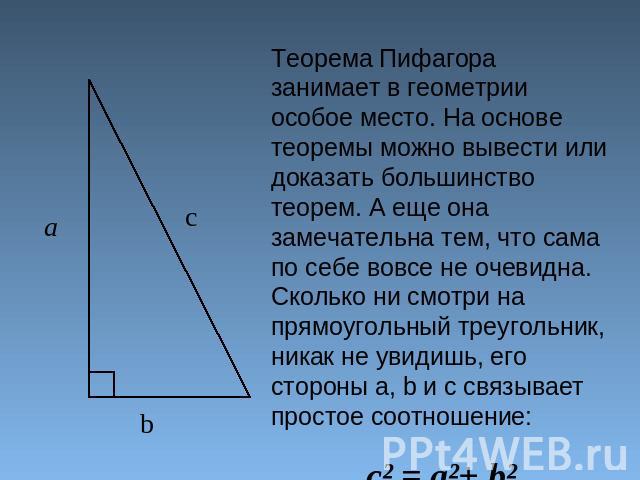
Теорема Пифагора занимает в геометрии особое место. На основе теоремы можно вывести или доказать большинство теорем. А еще она замечательна тем, что сама по себе вовсе не очевидна. Сколько ни смотри на прямоугольный треугольник, никак не увидишь, его стороны а, b и с связывает простое соотношение:c² = a²+ b²

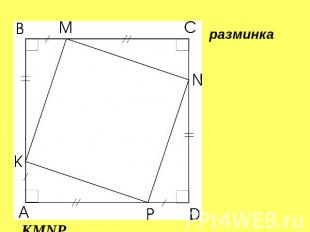
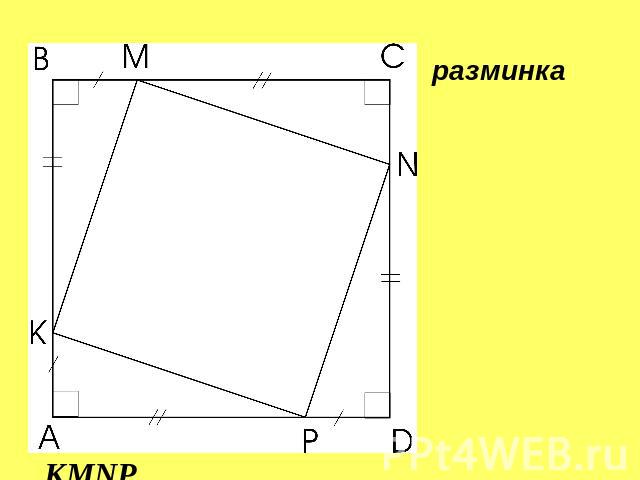
разминка

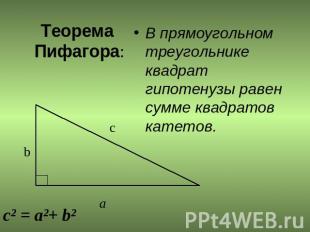
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.c² = a²+ b²

Забавное стихотворение , которое помогает запомнить формулировку теоремы Пифагора. Если дан нам треугольник,И при том с прямым углом,То квадрат гипотенузыМы всегда легко найдем:Катеты в квадрат возводим,Сумму степеней находим – И таким простым путем К результату мы придем.

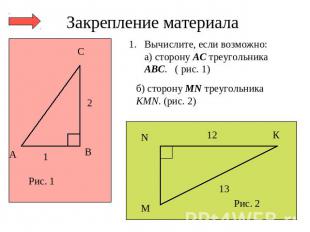
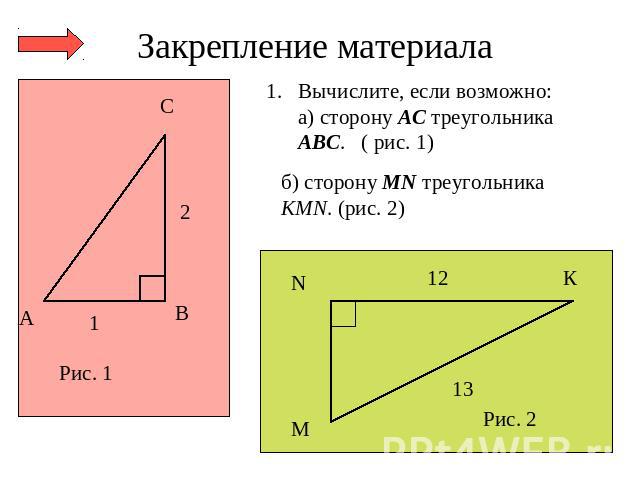
Закрепление материала Вычислите, если возможно:а) сторону АС треугольника АВС. ( рис. 1)б) сторону МN треугольника КМN. (рис. 2)

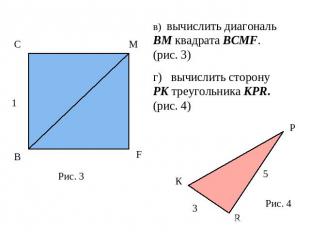
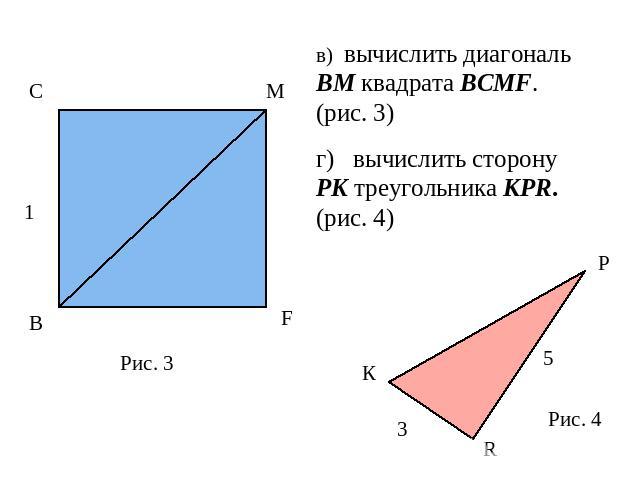
в) вычислить диагональ ВМ квадрата ВСМF. (рис. 3)г) вычислить сторону PK треугольника КPR. (рис. 4)

Решение старинных задач Задача индийского математика XII в. Бхаскары.На берегу реки рос тополь одинокий.Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял.Запомни теперь, что в том месте рекаВ четыре лишь фута всего широка.Верхушка склонилась у края реки,Осталось три фута всего от ствола.Прошу тебя, скоро теперь мне скажи:У тополя как велика высота?

Найти высоту тополя, если ширина реки 4 фута, а ствол надломился на высоте 3 фута.

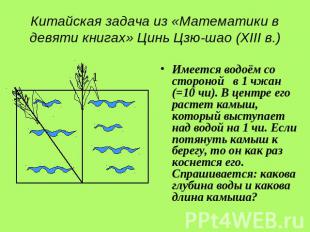
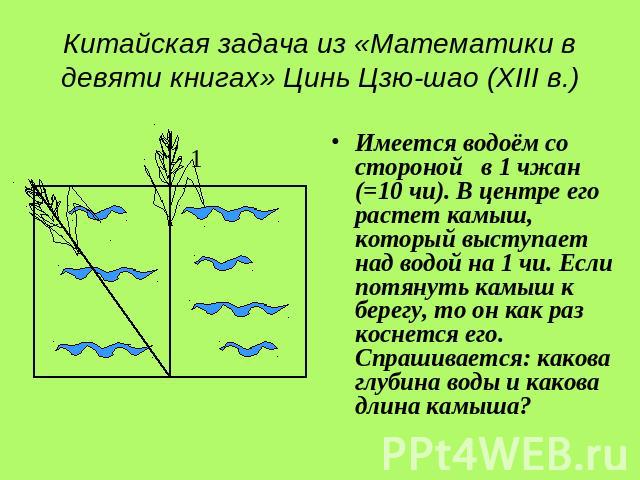
Китайская задача из «Математики в девяти книгах» Цинь Цзю-шао (XIII в.) Имеется водоём со стороной в 1 чжан (=10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?

Если, обозначить глубину воды через х, то получим прямоугольный треугольник, один катет которого есть х, второй равен 5, а гипотенуза х+1. (x+1)²=5²+x²x²+2х+1=5²+x²2х =25 – 12х = 24х = 12.

Домашнее задание: п. 54, №483 а), 485.