Презентация на тему: Площади плоских фигур

Игра"Интеллектуальное казино"урок по геометрии в 8 классе по теме "Площади плоских фигур"МБОУ «Первомайская СОШ» Оренбургского района Оренбургской области Учитель математики Газизова В.В.

Цель:Обобщить и систематизировать знания учащихся по теме «Площади плоских фигур»:Повторить определения и свойства фигур, формулы для вычисления площади.Совершенствовать навыки решения задач.Развивать смекалку и навык применения знаний математики в различных ситуациях.

правила игры В игре могут участвовать несколько команд, по 2 или 3 человека в каждой. Команды по очереди выбирают задания различной сложности. Если команда даёт правильный ответ, то её капитал увеличивается на стоимость задания, то есть на 5; 10; 15 или 20 умов. На обдумывание задания даётся 1- 5 минут.Игрок может взять подсказку для решения задачи II уровня, при этом стоимость задачи уменьшится в 2 раза. Победителем объявляется тот, в чьём банке будет больше «умов» по окончанию игры.

Загадки и определенияСвойства иформулыЗадачи I уровняЗадачи II уровня

1.Хоть стороны мои Попарно и равны, И параллельны, Всё же я в печали, Что не равны мои диагонали, Да и углы они не делят пополам. А кто я, догадайся сам.2.Дайте определение данной фигуры.

1.А у меня равны диагонали, Вам подскажу я, чтоб меня узнали. И хоть я не зовусь квадратом, Считаю я себя квадрата братом.2.Дайте определение этой фигуры.

1.Мои хотя и не равны диагонали, По значимости всем я уступлю едва ли. Ведь под прямым углом они пересекаются,И каждый угол делят пополам!2. Дайте определение этой фигуры.

1.Первая- такой многоугольник, Знать который должен каждый школьник. На второй гимнасты выступают, Их она под купол поднимает.2. Дайте определение этой фигуры.

1.Нет углов у меня И похож на блюдце я. На тарелку и на крышку, На кольцо, на колесо, Кто же я такой, друзья?2.Дайте определение этой фигуры.

1.Перечислите свойства квадрата.2. Напишите формулу для вычисления его площади.

1.Перечислите свойства параллелограмма.2. Запишите формулу для вычисления его площади.

1.Перечислите свойства трапеции.2.Напишите формулу для вычисления её площади.

1.Сформулируйте свойства прямоугольника.2. Запишите формулу для вычисления его площади.

Какая связь между радиусом круга и диаметром?Запишите формулу для нахождения площади круга.

1.Сформулируйте свойства ромба.2.Запишите формулу для вычисления его площади.

Сформулируйте свойства равнобедренного треугольника.Запишите формулу для вычисления площади произвольного треугольника.

Дано: АВСD -параллелограмм; АВ=7см; АD=10см; угол ВАD= 30°Найти: площадь пар-ма АВСD.Решение: проведём высоту ВН к стороне АD.В ∆АВН катет ВН лежит против гипотенузы АВ.ВН=½АВ=3,5см; S= ah = 3,5*10=35см2Ответ: 3,5см2

Дано: АВСD-квадрат;SАВСD = 81см2СЕ=2 см;Найти: площадь Трапеции АВСЕ. Решение: обозначим сторону квадрата за a см. Sкв=a2 ,Поэтому a2=81, отсюда a=9;SтрАВСЕ= ½ (9+2)*9=49,5см2Ответ: 49,5см2

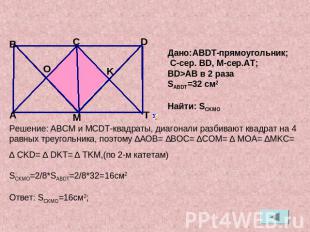
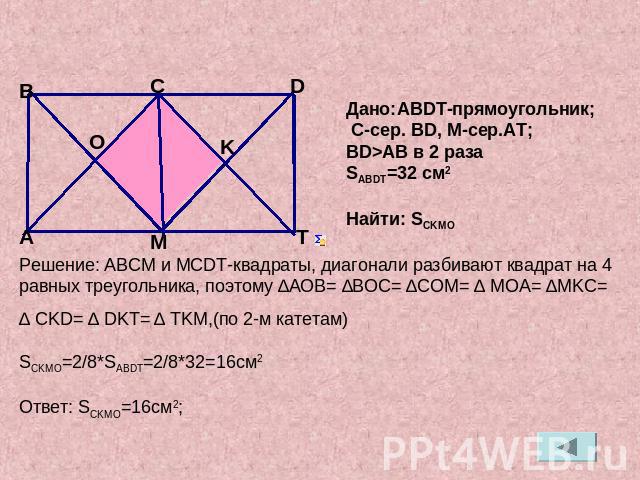
Дано:ABDT-прямоугольник; C-сер. BD, М-сер.AT;BD>AB в 2 разаSABDT=32 см2Найти: SCKMOРешение: АВСМ и МСDT-квадраты, диагонали разбивают квадрат на 4 равных треугольника, поэтому ∆АОВ= ∆ВОС= ∆СOМ= ∆ МOA= ∆MKC= ∆ CKD= ∆ DKT= ∆ TKM,(по 2-м катетам)SCKMO=2/8*SABDT=2/8*32=16см2Ответ: SCKМО=16см2;

Дано: АВСP-квадрат,АB=12 cм,F-середина СP;Найти: S ∆ABDРешение: ∆AFP= ∆DFC по II признаку равенства треугольников, значит S ∆AFP=S ∆DFC ;S ∆ABD=SABCF+S ∆ DFC=SABCF+S ∆AFP=sABCP=122=144cм2Ответ: SABCP=144cм2

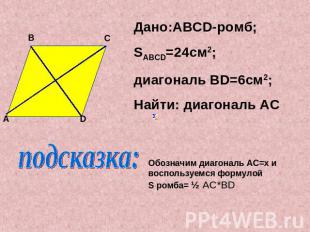
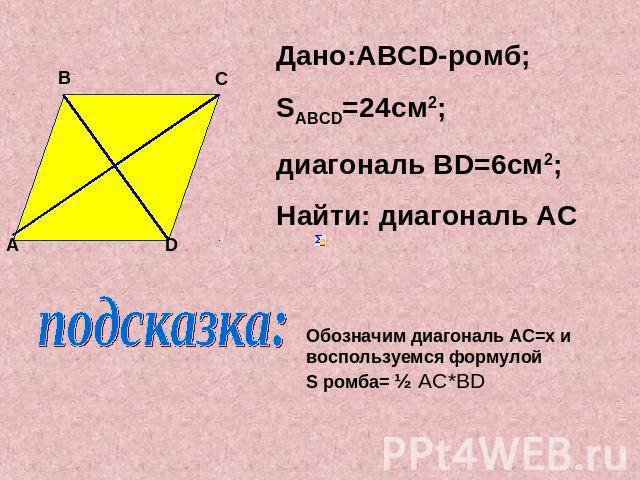
Дано:ABCD-ромб;SABCD=24см2;диагональ ВD=6см2;Найти: диагональ ACпОбозначим диагональ AC=x и воспользуемся формулойS ромба= ½ AC*BD

Решение: пусть AC=X cм, подставим в формулу S ромба= ½ AC*BD, получим:½X*6=24;3X=24;X=8Ответ: AC=8cм;

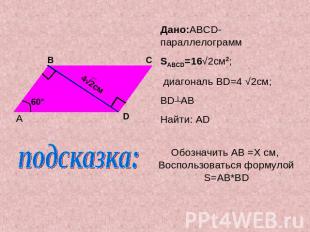
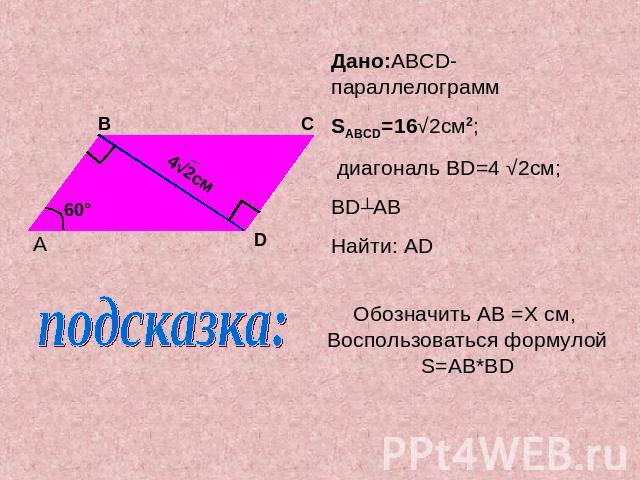
Дано:ABCD-параллелограмм SABCD=16√2см2; диагональ BD=4 √2см;BD┴ABНайти: ADОбозначить AB =X cм, Воспользоваться формулойS=AB*BD

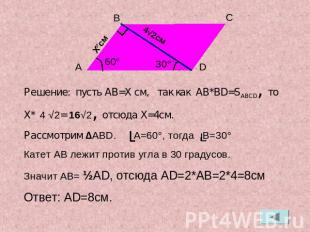
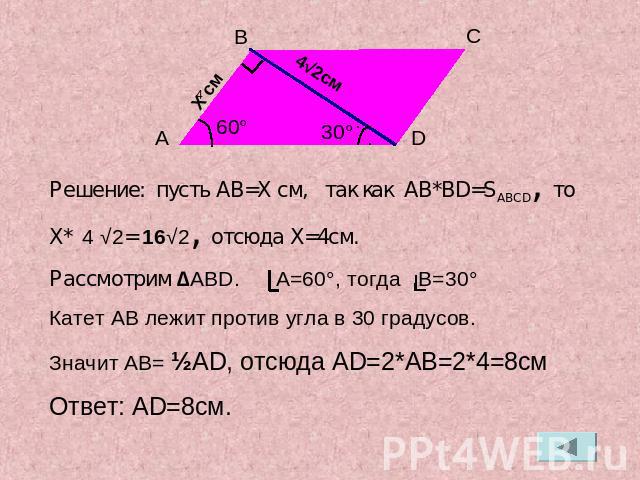
Решение: пусть AB=X см, так как AB*BD=SABCD, то X* 4 √2= 16√2, отсюда X=4см.Рассмотрим ∆ABD. A=60°, тогда B=30°Катет AB лежит против угла в 30 градусов. Значит AB= ½AD, отсюда AD=2*AB=2*4=8смОтвет: AD=8см.

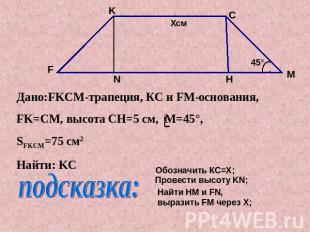
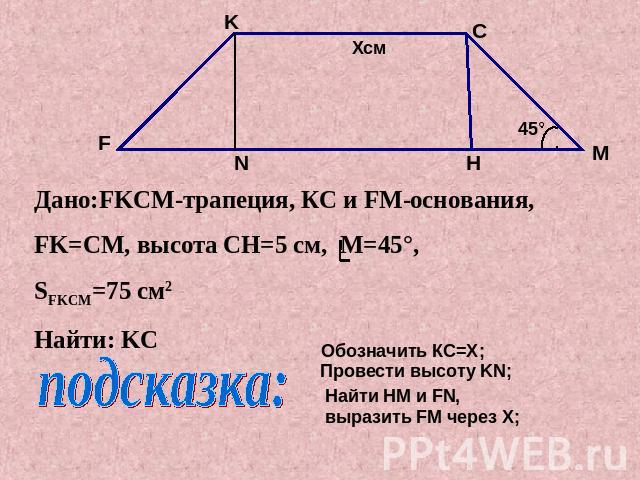
Дано:FKCM-трапеция, КС и FM-основания,FK=CМ, высота CH=5 см, M=45°,SFKCM=75 см2Найти: KC Обозначить КС=X;Провести высоту KN;Найти HM и FN, выразить FM через X;

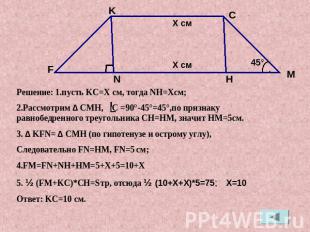
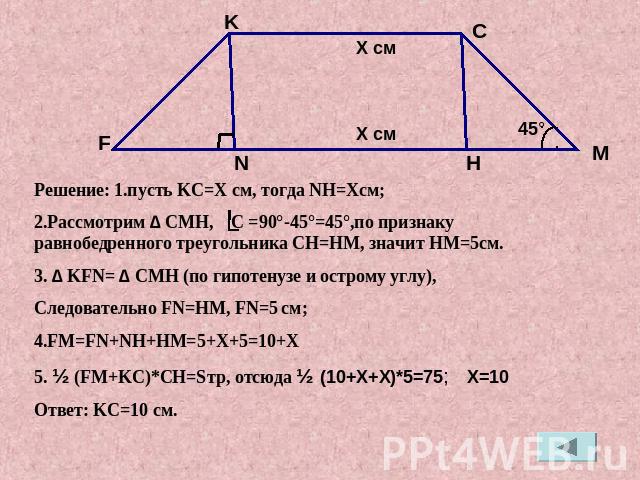
Решение: 1.пусть KC=X см, тогда NH=Xсм;2.Рассмотрим ∆ CMH, C =90°-45°=45°,по признаку равнобедренного треугольника CH=HM, значит HM=5см.3. ∆ KFN= ∆ CMH (по гипотенузе и острому углу), Следовательно FN=HM, FN=5 см;4.FM=FN+NH+HM=5+X+5=10+X5. ½ (FM+KC)*CH=Sтр, отсюда ½ (10+X+X)*5=75; X=10Ответ: KC=10 см.

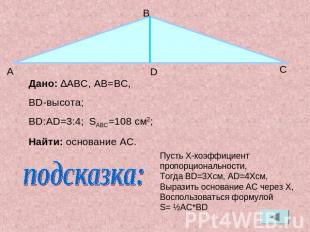
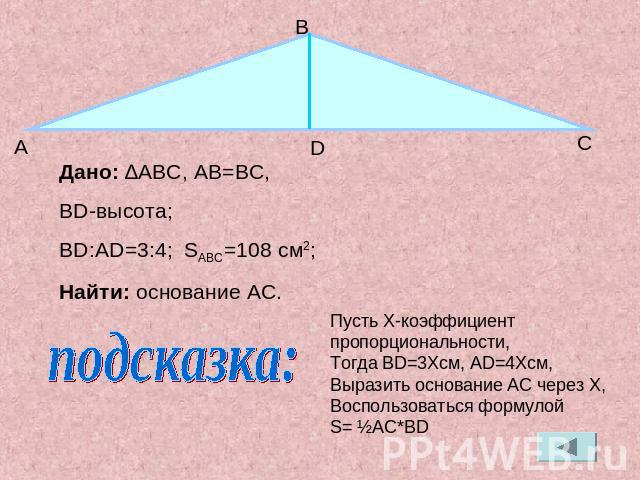
Дано: ∆ABC, АB=BC,BD-высота;BD:AD=3:4; SABC=108 см2;Найти: основание AC.Пусть X-коэффициент пропорциональности,Тогда BD=3Xсм, АD=4Xсм, Выразить основание AC через X,Воспользоваться формулой S= ½AC*BD

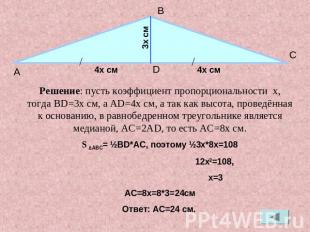
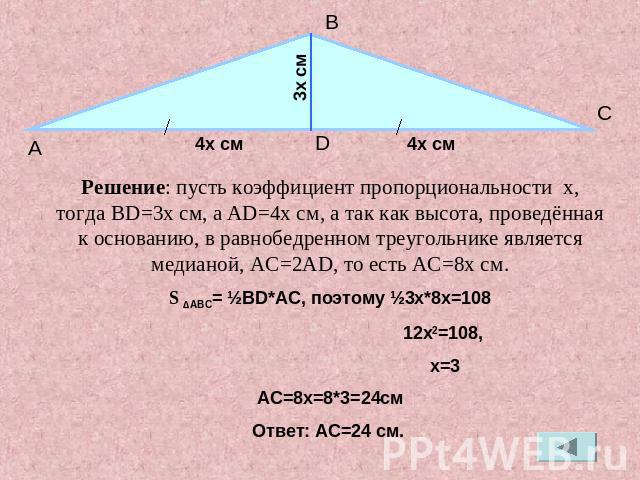
Решение: пусть коэффициент пропорциональности x, тогда BD=3x см, а AD=4x cм, а так как высота, проведённая к основанию, в равнобедренном треугольнике является медианой, AC=2AD, то есть AC=8x cм.S ∆ABC= ½BD*AC, поэтому ½3x*8x=108 12x2=108, x=3АС=8x=8*3=24cмОтвет: AC=24 cм.

Ребята, вы молодцы!!!

Ребята, вы молодцы!!!