Презентация на тему: Чевианы треугольника. Свойства медиан

Чевианы треугольникаСвойства медиан

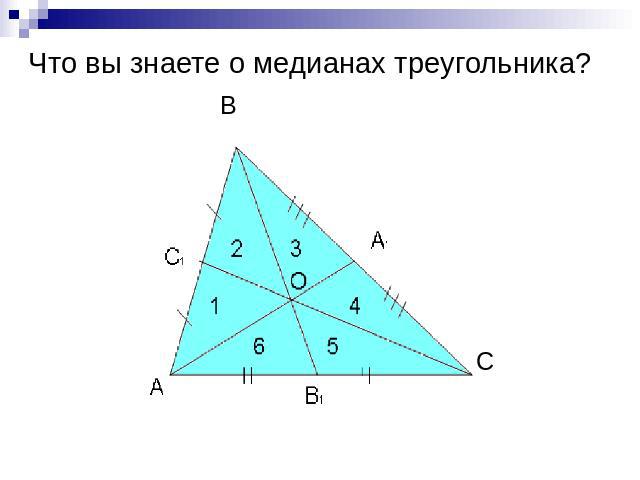
Что вы знаете о медианах треугольника?

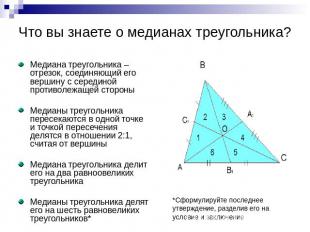
Что вы знаете о медианах треугольника? Медиана треугольника – отрезок, соединяющий его вершину с серединой противолежащей стороны Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины Медиана треугольника делит его на два равноовеликих треугольника Медианы треугольника делят его на шесть равновеликих треугольников* *Сформулируйте последнее утверждение, разделив его на условие и заключение

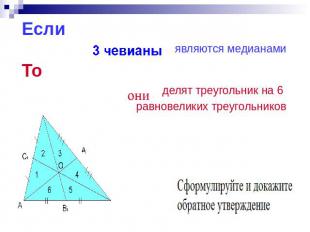
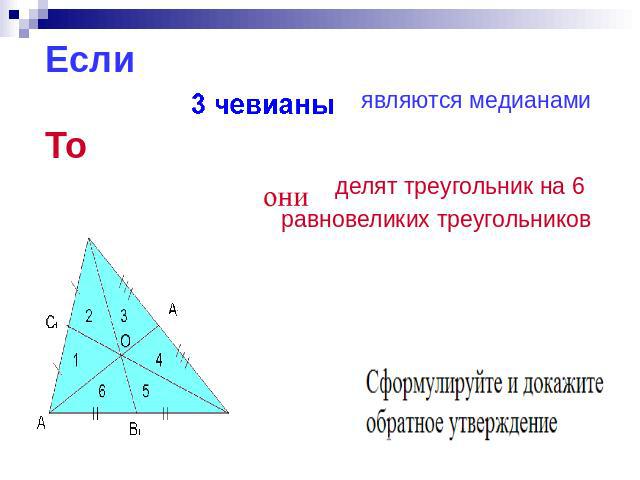
Если являются медианами То делят треугольник на 6 равновеликих треугольников

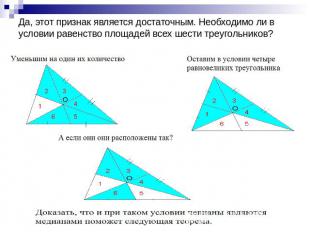
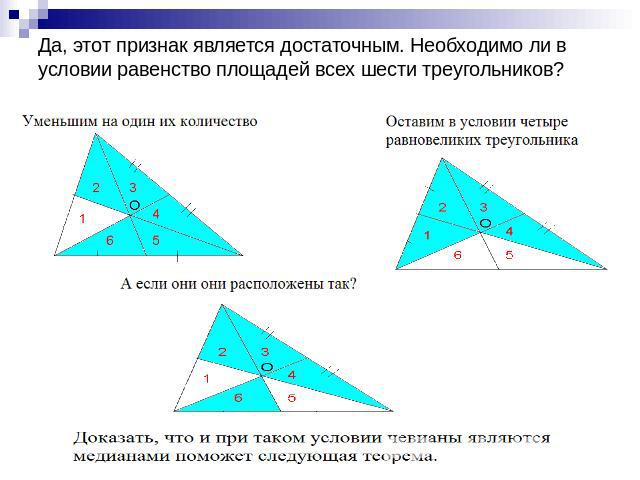
Да, этот признак является достаточным. Необходимо ли в условии равенство площадей всех шести треугольников?

Критерий точки медианы

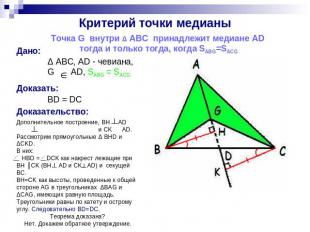
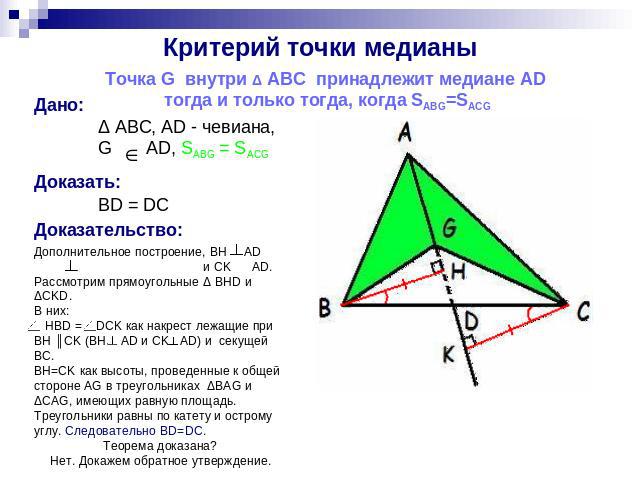
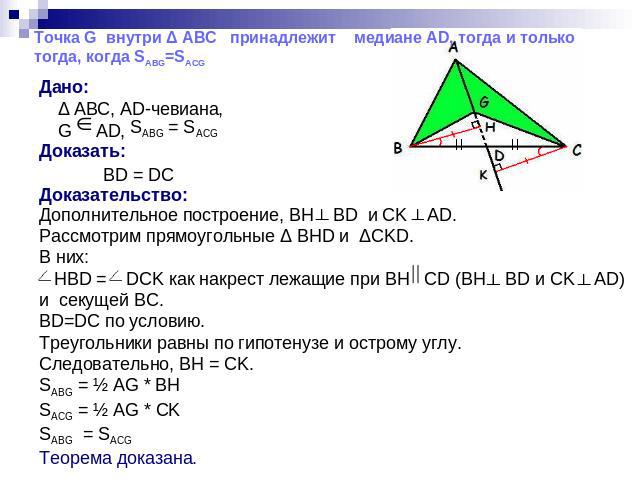
Критерий точки медианы Точка G внутри Δ АВС принадлежит медиане AD тогда и только тогда, когда SABG=SACG Дано: Δ ABC, AD - чевиана, G ADДоказать: BD = DC , SABG = SACG Доказательство: Дополнительное построение, BH AD и CK AD. Рассмотрим прямоугольные Δ BHD и ΔСKD. В них: НBD = DCK как накрест лежащие при BH ║CK (BH AD и CK AD) и секущей BC. ВH=CK как высоты, проведенные к общей стороне AG в треугольниках ΔBAG и ΔCAG, имеющих равную площадь. Треугольники равны по катету и острому углу. Следовательно BD=DC. Теорема доказана? Нет. Докажем обратное утверждение.

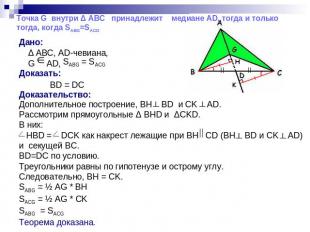
Точка G внутри Δ АВС принадлежит медиане AD, тогда и только тогда, когда SABG=SACG Дано: Δ ABC, AD-чевиана, G AD, Доказать: BD = DC Доказательство: Дополнительное построение, BH BD и CK AD. Рассмотрим прямоугольные Δ BHD и ΔСKD. В них: НBD = DCK как накрест лежащие при BH CD (BH BD и CK AD) и секущей BC. BD=DC по условию. Треугольники равны по гипотенузе и острому углу. Следовательно, BH = CK. SABG = ½ AG * BH SACG = ½ AG * CK SABG = SACG Теорема доказана.

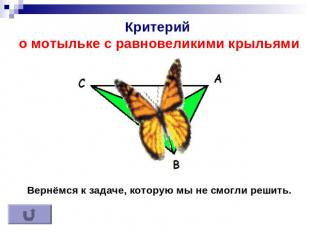
Критерий о мотыльке с равновеликими крыльями Вернёмся к задаче, которую мы не смогли решить.

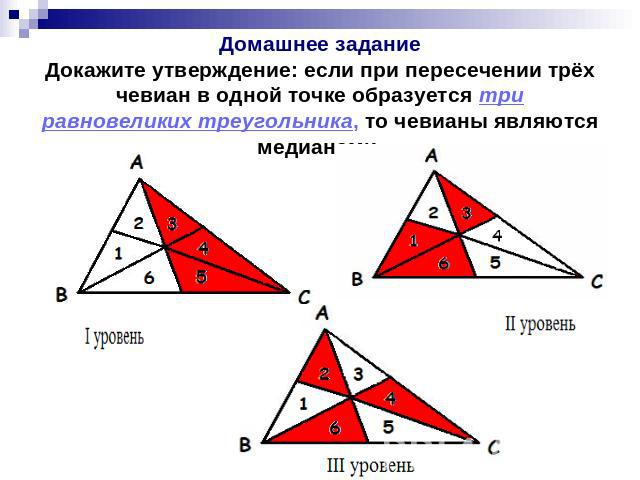
Домашнее заданиеДокажите утверждение: если при пересечении трёх чевиан в одной точке образуется три равновеликих треугольника, то чевианы являются медианами.

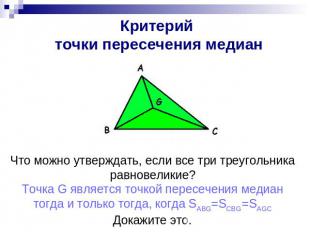
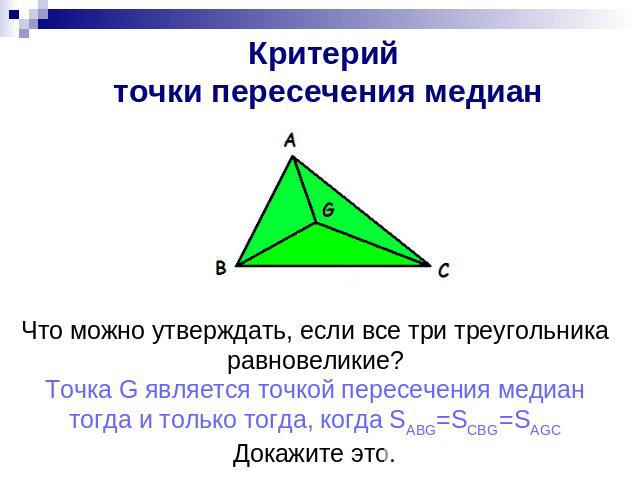
Критерий точки пересечения медиан Что можно утверждать, если все три треугольника равновеликие? Точка G является точкой пересечения медиан тогда и только тогда, когда SABG=SCBG=SAGC Докажите это.

Задача На каком расстоянии от стороны треугольника, равной 12 см, находится его центр масс, если от стороны, равной 18 см, он находится на расстоянии 4 см?