Презентация на тему: Чевианы треугольникаСвойства медиан

Чевианы треугольника Свойства медиан
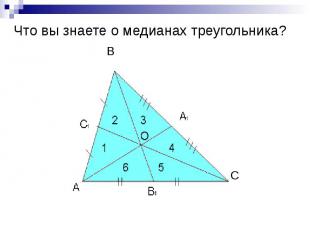
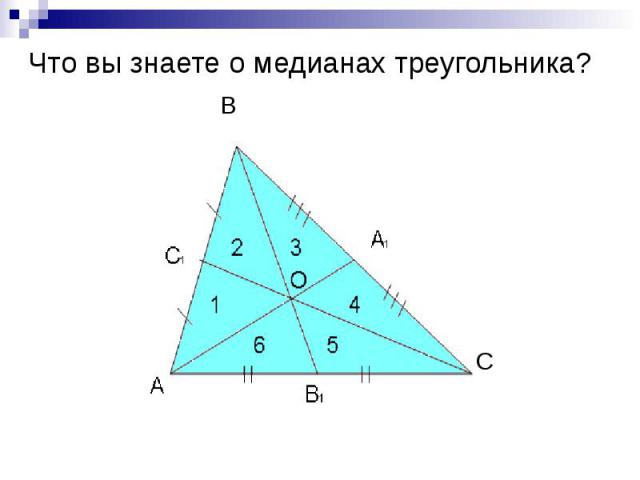
Что вы знаете о медианах треугольника?
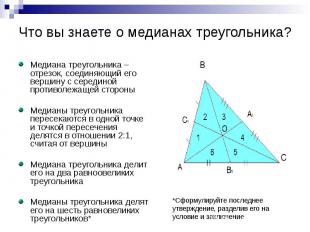
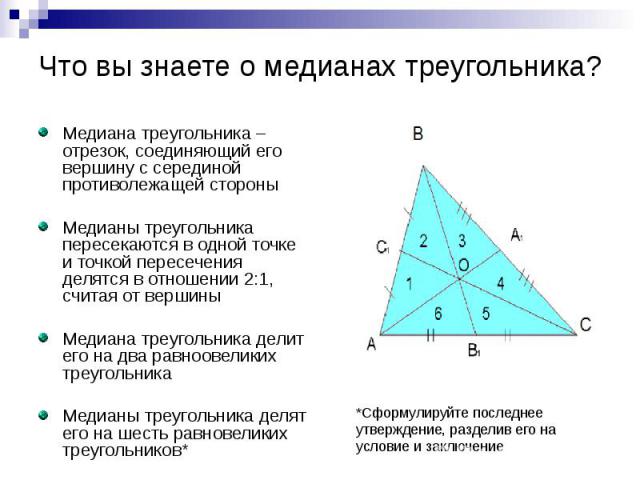
Что вы знаете о медианах треугольника? Медиана треугольника – отрезок, соединяющий его вершину с серединой противолежащей стороны Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины Медиана треугольника делит его на два равноовеликих треугольника Медианы треугольника делят его на шесть равновеликих треугольников*
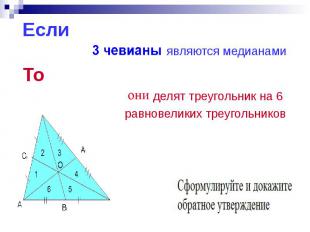
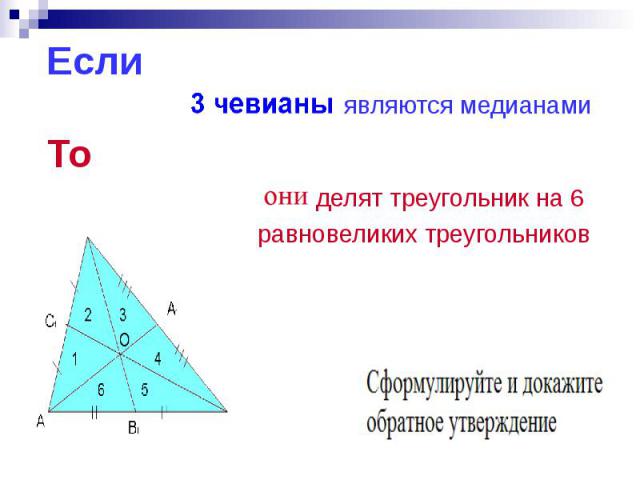
Если Если являются медианами То делят треугольник на 6 равновеликих треугольников
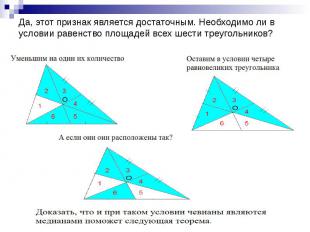
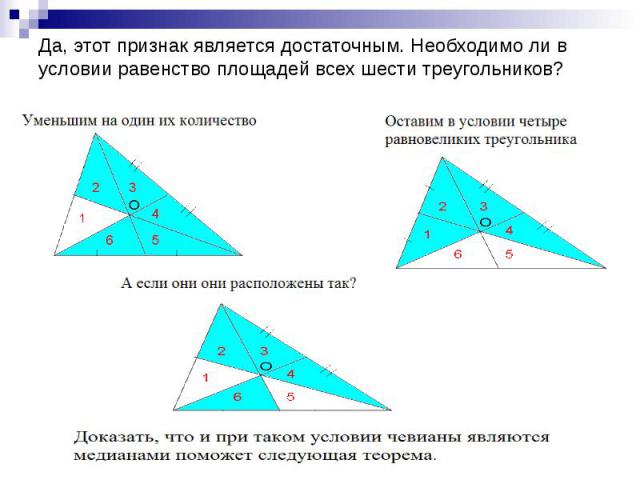
Да, этот признак является достаточным. Необходимо ли в условии равенство площадей всех шести треугольников?

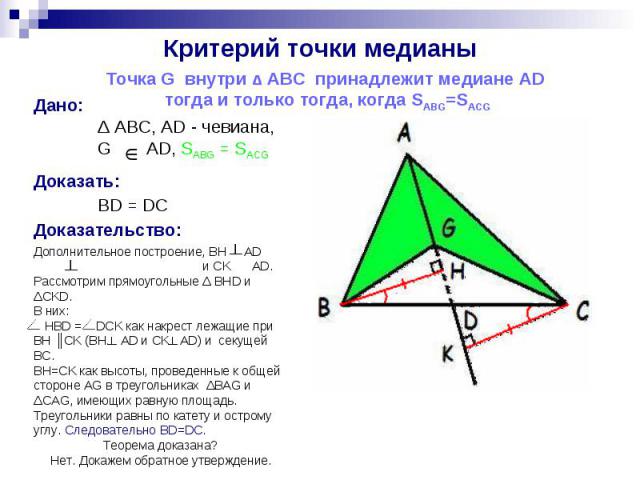
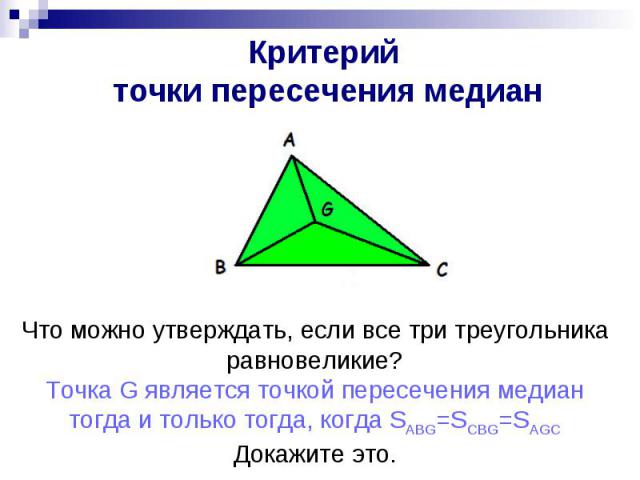
Критерий точки медианы
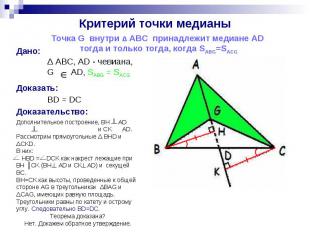
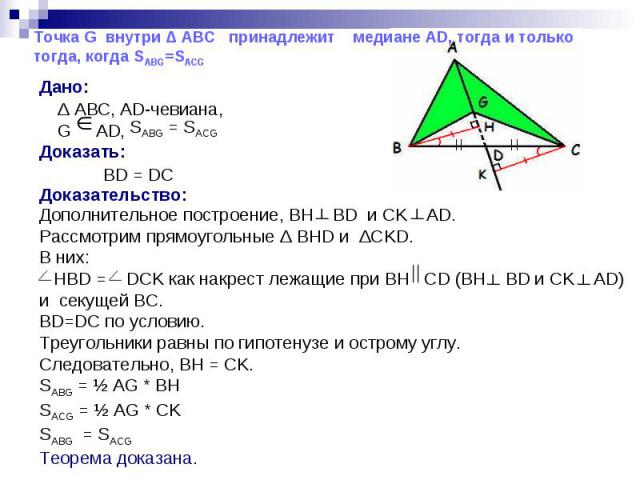
Дано: Δ ABC, AD - чевиана, G AD, SABG = SACG

Дано: Дано: Δ ABC, AD-чевиана, G AD,
Критерий точки медианы
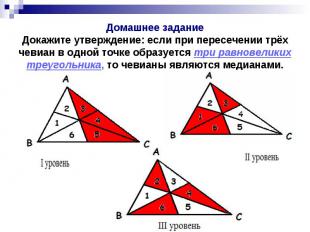
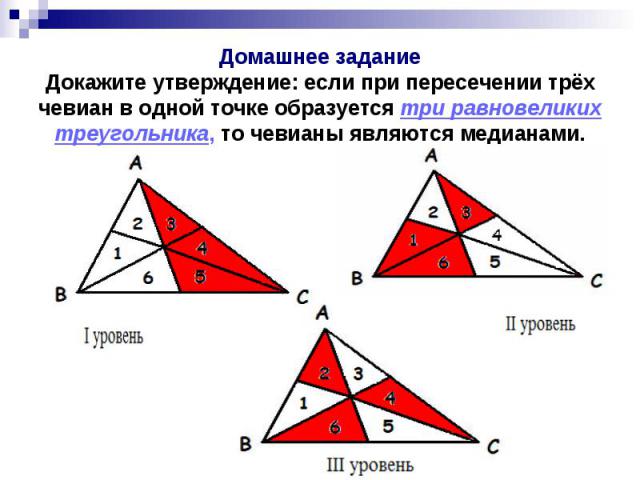
Домашнее задание Докажите утверждение: если при пересечении трёх чевиан в одной точке образуется три равновеликих треугольника, то чевианы являются медианами.
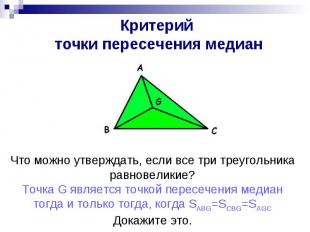
Критерий точки медианы

Задача На каком расстоянии от стороны треугольника, равной 12 см, находится его центр масс, если от стороны, равной 18 см, он находится на расстоянии 4 см?