Презентация на тему: Квадратичная функция и её график

Квадратичная функция и её график

График функции y = ax2. График функции y = ax2 + bx + c. Лабораторно-графическая работа

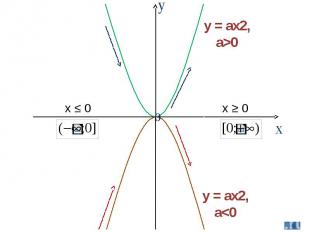
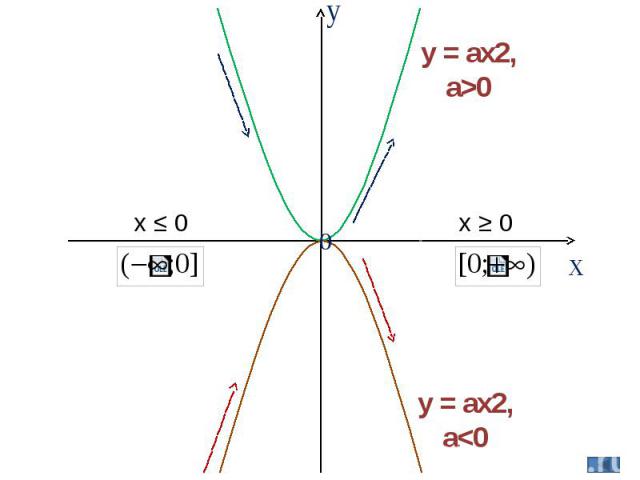
y = ax2, a>0 y = ax2, a

Задача: Построить график функции y = x2 – 2x + 3 и сравнить с графиком функции y = x2 Построение.Графиком функции y = x2 – 2x + 3 является парабола, ветви которой направлены вверх.Составим таблицу значений функции y = x2 – 2x + 3 Построим график функции y = x2 – 2x + 3 Сравним графики y = x2 – 2x + 3 и y = x2 y = x2 – 2x + 3 = x2 – 2x + 1+ 2 = (x – 1)2 + 2 Вывод: Графиком функции y = x2 – 2x + 3 является парабола, получаемая сдвигом параболы y = x2 на единицу вправо и на две единицы вверх.

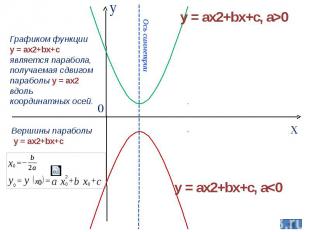
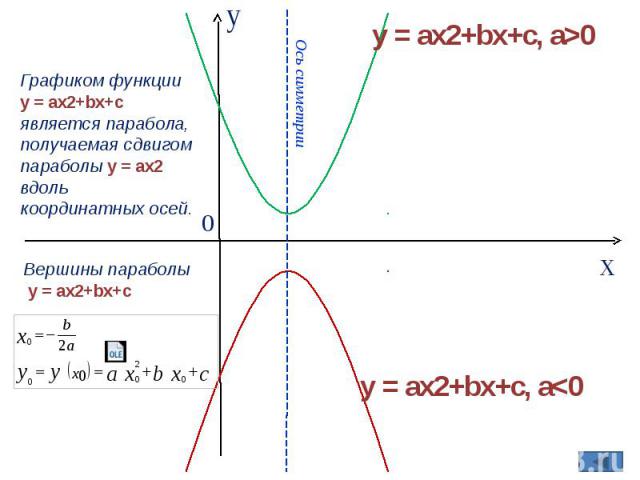
Графиком функции y = ax2+bx+c является парабола, получаемая сдвигом параболы y = ax2 вдоль координатных осей. Вершины параболы y = ax2+bx+c Ось симметрии y = ax2+bx+c, a>0 y = ax2+bx+c, a

ЗаданияДана функция y = ax2 +bx + c.Найдите координаты точек пересечения графика функции с осями координат.Постройте график данной функции.С помощью графика найдите: множество значений х, на котором функция: 1) возрастает, 2) убывает, 3) принимает положительные значения, 4) принимает отрицательные значения;значения переменной х, при которых функция принимает наибольшее и наименьшее значение.Проходит ли график данной функции через точки A(m; n), B(-m; n), C(-m; -n), D(m; -n).

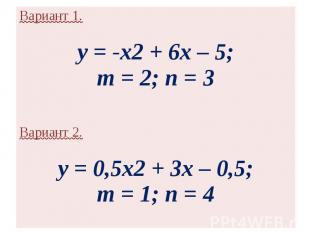
Вариант 1.y = -x2 + 6x – 5;m = 2; n = 3 Вариант 2.y = 0,5x2 + 3x – 0,5;m = 1; n = 4