Презентация на тему: Квадратичная функция. Ее свойства и график

Квадратичная функция. Её свойства и график.

1. Определить, какие из данных функций являются квадратичными: 1. Определить, какие из данных функций являются квадратичными:

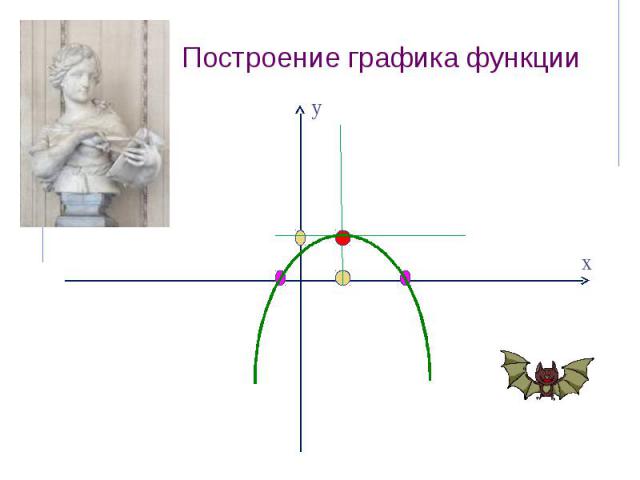
Алгоритм построения параболы у = ах2 + bх + с : Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось симмертрии. Определить направление ветвей параболы. Найти координаты еще нескольких точек , принадлежащих искомому графику ( в частности, координаты точки пересечения параболы с осью у и нули функции, если они существуют). Отметить на координатной плоскости найденные точки и соединить их плавной линией.

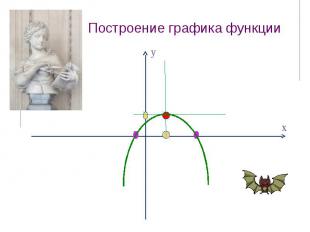
Построение графика функции

Мы уже строили графики функций вида Мы уже строили графики функций вида у = ах2 + bх + с , выделяя квадрат двучлена. Используем этот прием в общем виде: ах2 + bx + с = а (х2 + x ) + с = = а + с = = а + с = а

Графиком квадратичной функции Графиком квадратичной функции у = ах2 + bх + с является парабола, которая получается из параболы у = ах2 параллельным переносом.

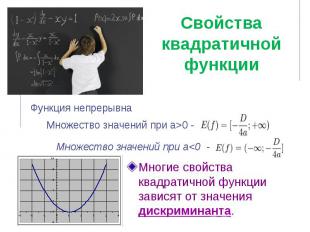
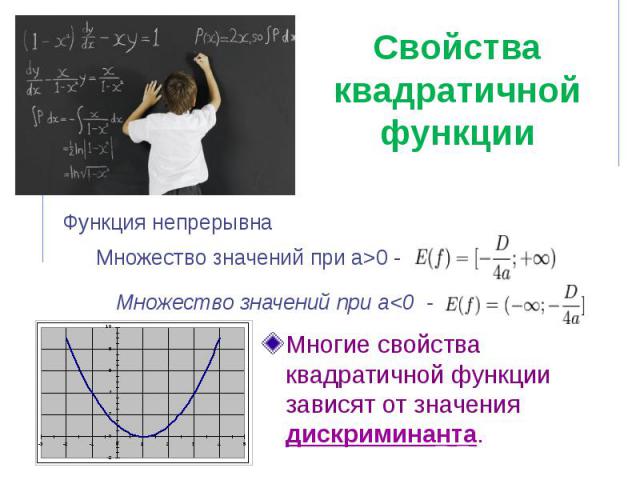
Свойства квадратичной функции Многие свойства квадратичной функции зависят от значения дискриминанта.

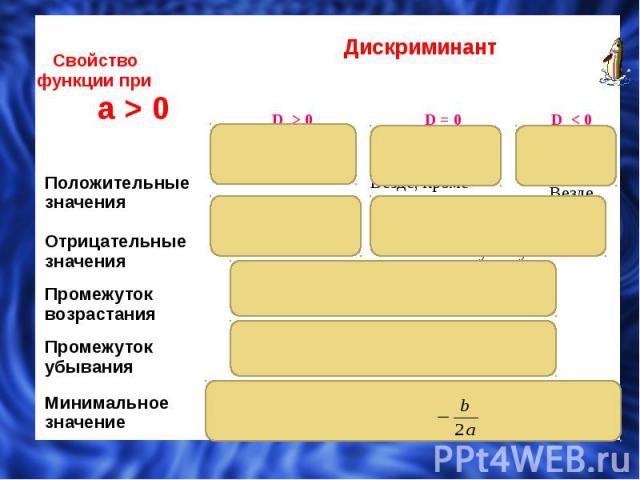
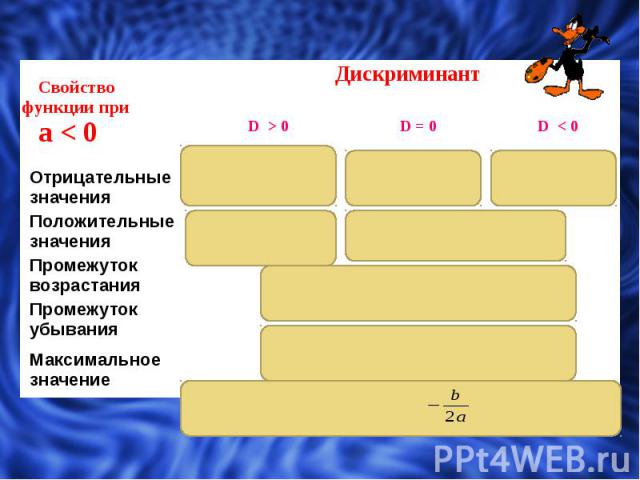
Вспоминаем : Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac Его обозначают буквой D, т.е. D= b2 – 4ac. Возможны три случая: D 0 D 0 D 0

   

   

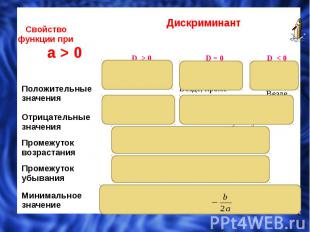
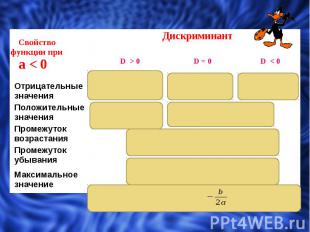
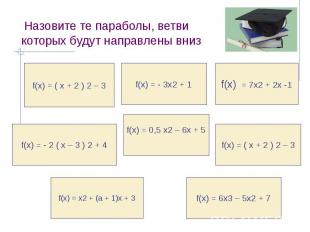
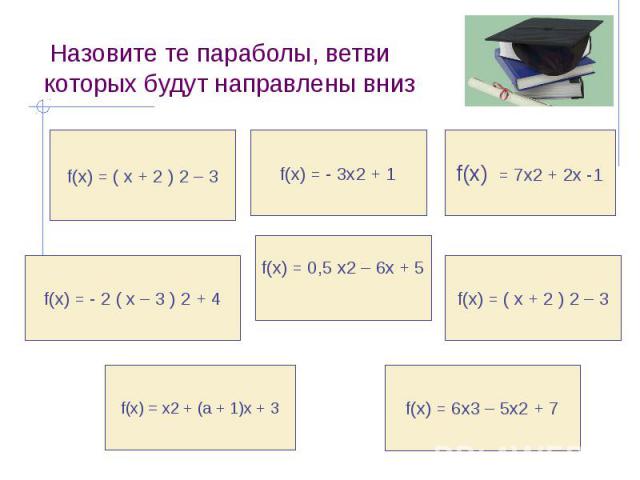
Назовите те параболы, ветви которых будут направлены вниз

Для закрепления теоретических знаний решим задачу.

Решение :

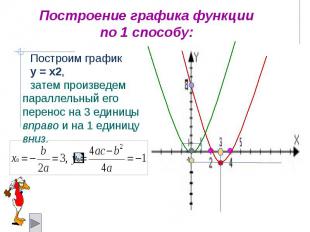
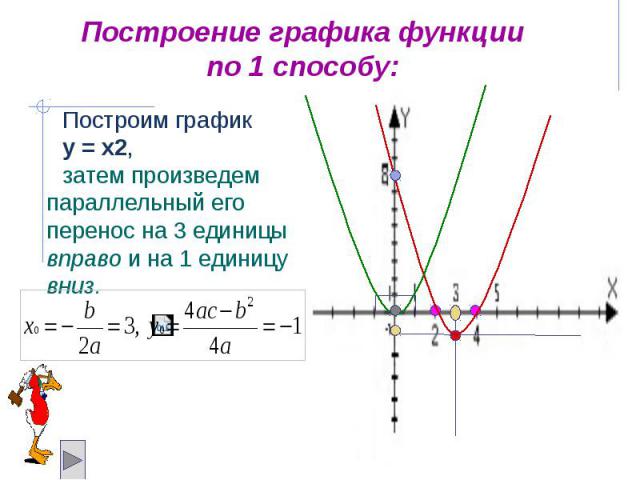
Построение графика функции по 1 способу:

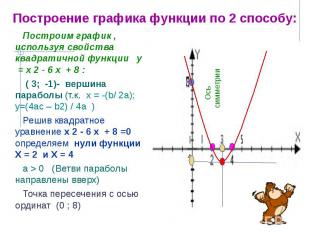
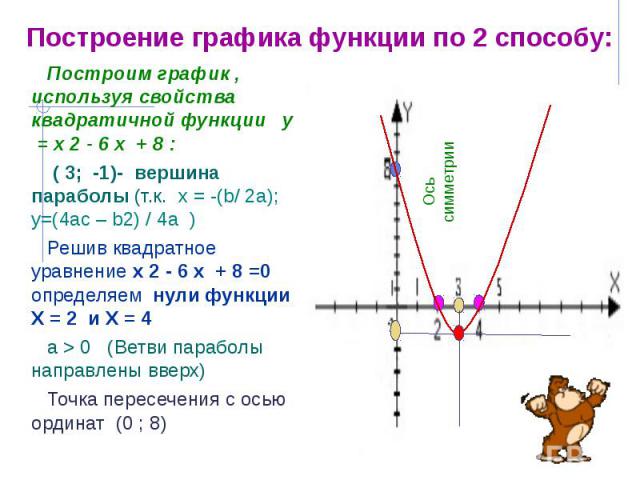
Построение графика функции по 2 способу:

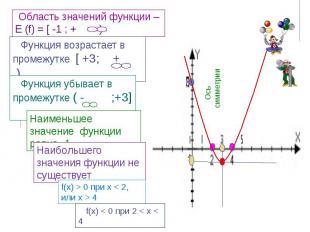
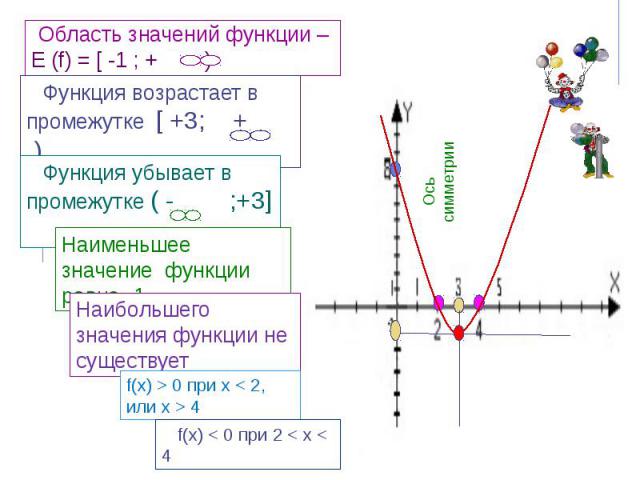
Область значений функции – Е (f) = [ -1 ; + )

Литература