Презентация на тему: Объем шара радиуса R выражается формулой

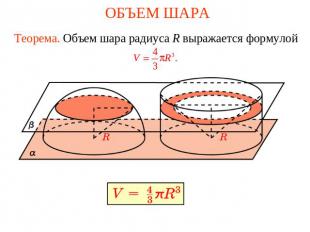
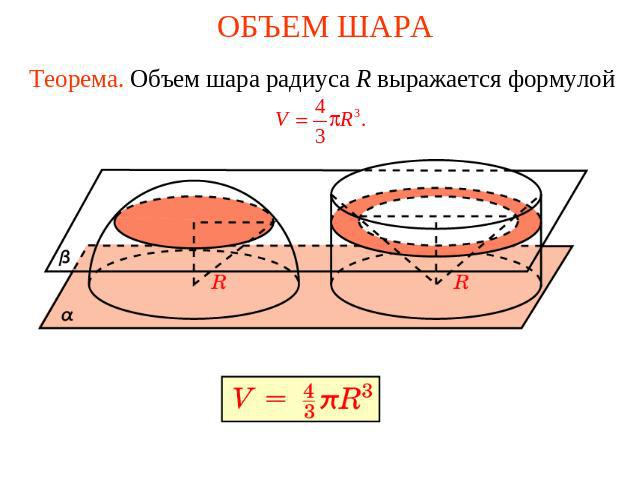
ОБЪЕМ ШАРА Теорема. Объем шара радиуса R выражается формулой

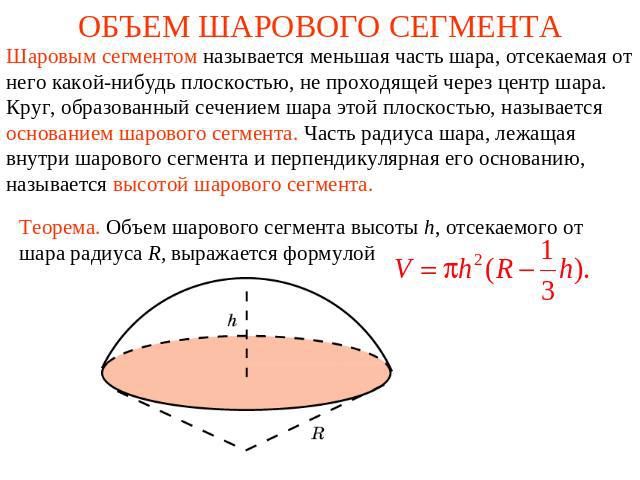
ОБЪЕМ ШАРОВОГО СЕГМЕНТА Шаровым сегментом называется меньшая часть шара, отсекаемая от него какой-нибудь плоскостью, не проходящей через центр шара. Круг, образованный сечением шара этой плоскостью, называется основанием шарового сегмента. Часть радиуса шара, лежащая внутри шарового сегмента и перпендикулярная его основанию, называется высотой шарового сегмента.Теорема. Объем шарового сегмента высоты h, отсекаемого от шара радиуса R, выражается формулой

ОБЪЕМ ШАРОВОГО СЕКТОРА Шаровым сектором называется часть шара, составленная из шарового сегмента и конуса, основанием которого является основание шарового сегмента, а вершиной - центр шара. Теорема. Объем шарового сектора радиуса R и углом при вершине выражается формулой

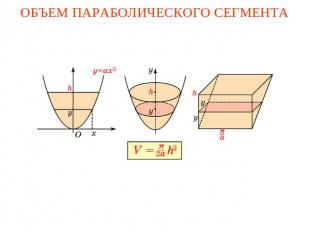
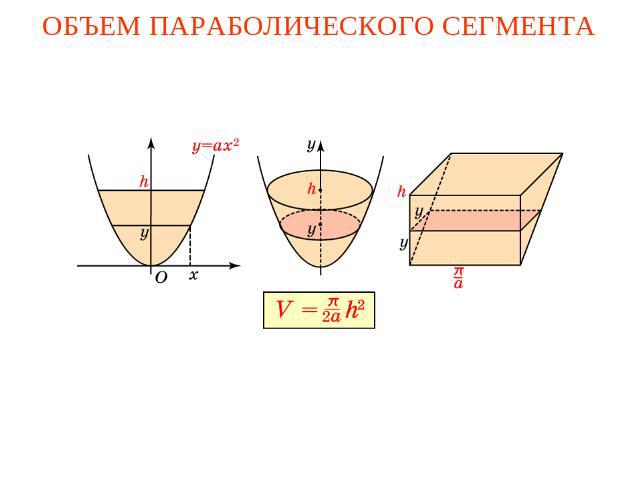
ОБЪЕМ ПАРАБОЛИЧЕСКОГО СЕГМЕНТА

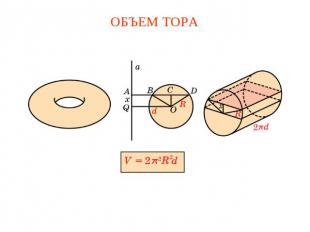
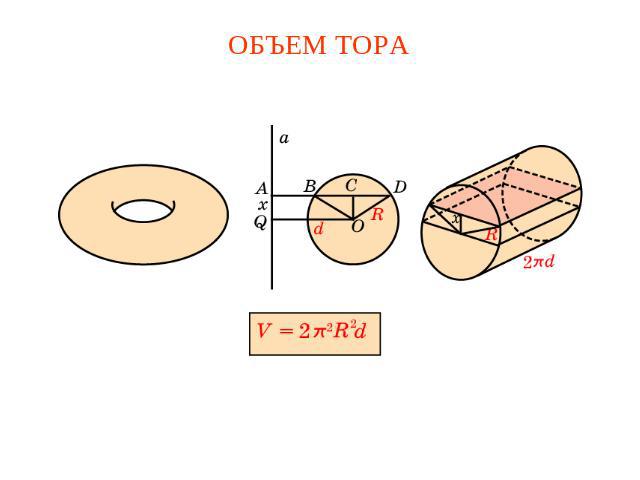
ОБЪЕМ ТОРА

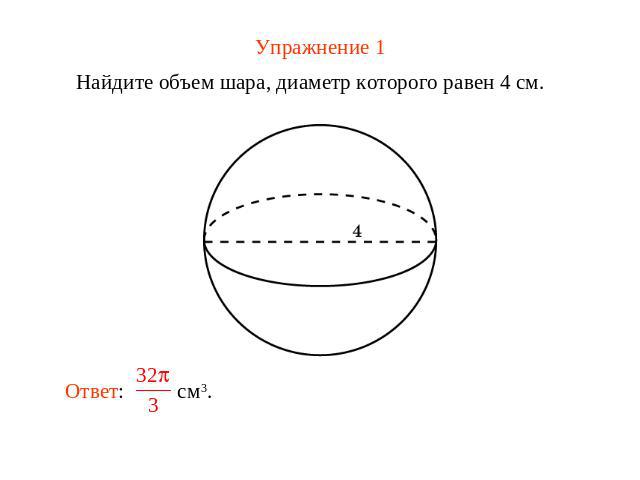
Упражнение 1 Найдите объем шара, диаметр которого равен 4 см.

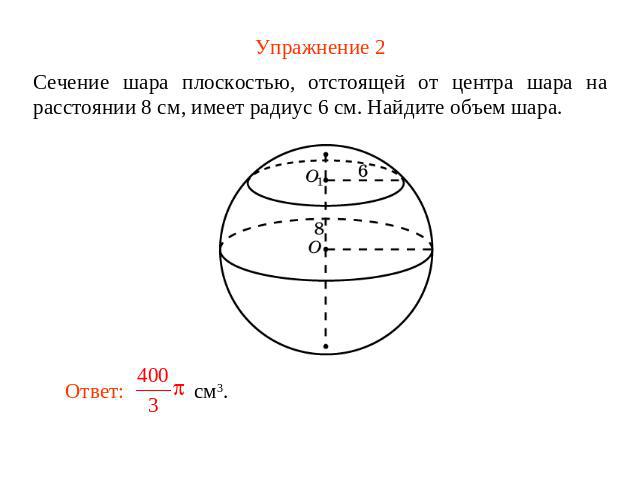
Упражнение 2 Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите объем шара.

Упражнение 3 Во сколько раз увеличится объем шара, если его радиус увеличить: а) в 3 раза; б) в 4 раза?

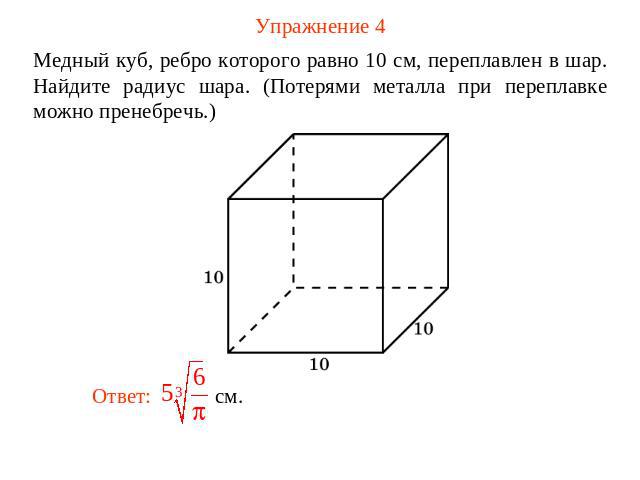
Упражнение 4 Медный куб, ребро которого равно 10 см, переплавлен в шар. Найдите радиус шара. (Потерями металла при переплавке можно пренебречь.)

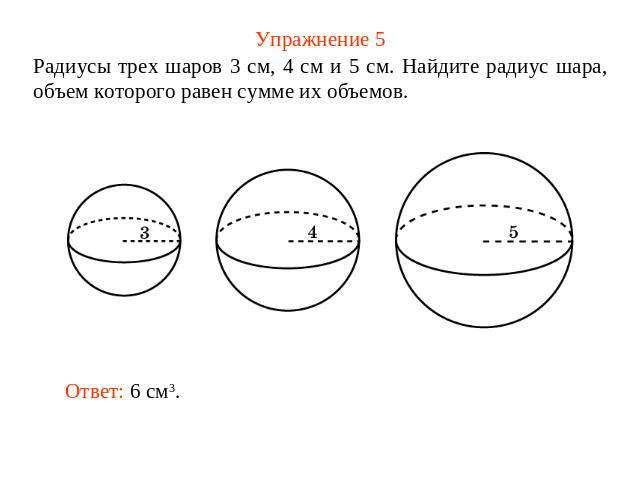
Упражнение 5 Радиусы трех шаров 3 см, 4 см и 5 см. Найдите радиус шара, объем которого равен сумме их объемов.

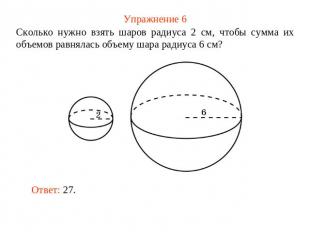
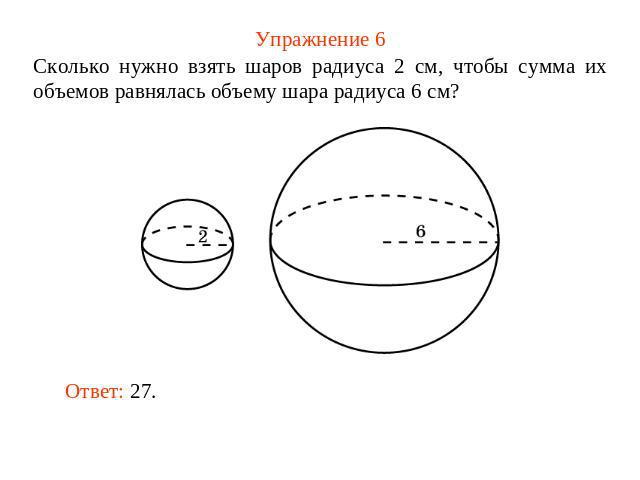
Упражнение 6 Сколько нужно взять шаров радиуса 2 см, чтобы сумма их объемов равнялась объему шара радиуса 6 см?

Упражнение 7 Найдите объем шара, вписанного в куб с ребром, равным единице.

Упражнение 8 Найдите объем шара, описанного около куба с ребром, равным единице.

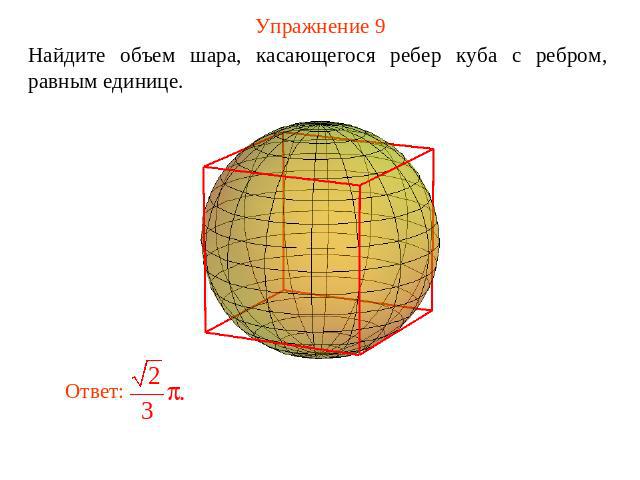
Упражнение 9 Найдите объем шара, касающегося ребер куба с ребром, равным единице.

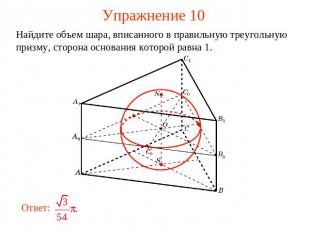
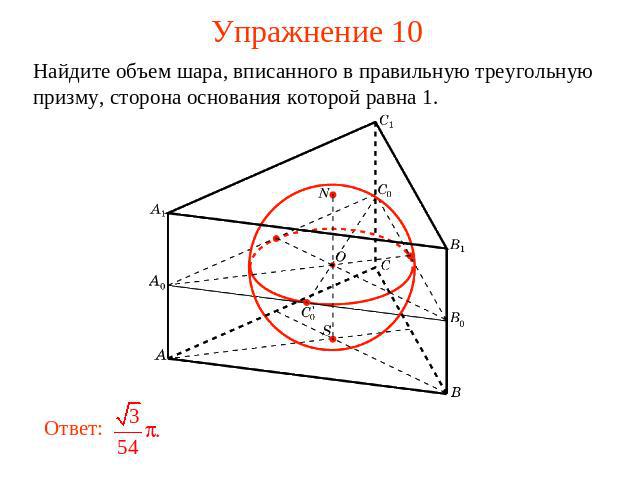
Упражнение 10 Найдите объем шара, вписанного в правильную треугольную призму, сторона основания которой равна 1.

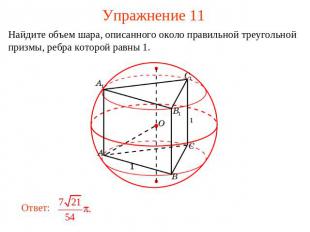
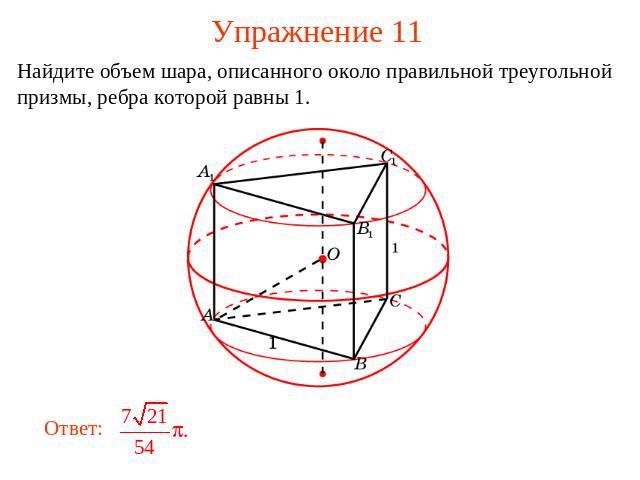
Упражнение 11 Найдите объем шара, описанного около правильной треугольной призмы, ребра которой равны 1.

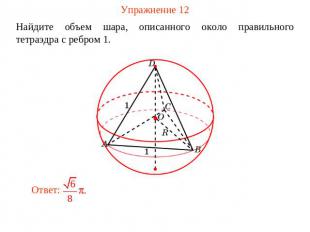
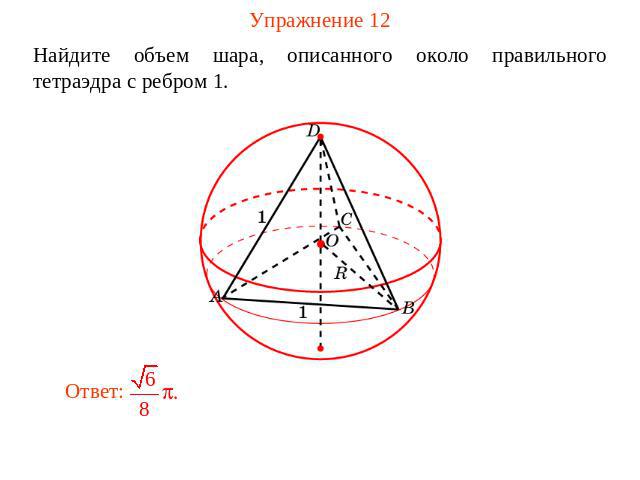
Упражнение 12 Найдите объем шара, описанного около правильного тетраэдра с ребром 1.

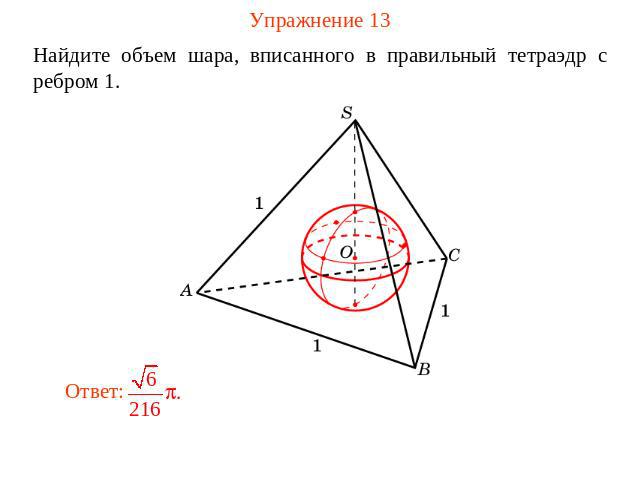
Упражнение 13 Найдите объем шара, вписанного в правильный тетраэдр с ребром 1.

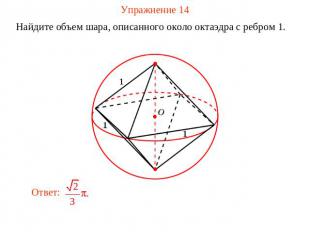
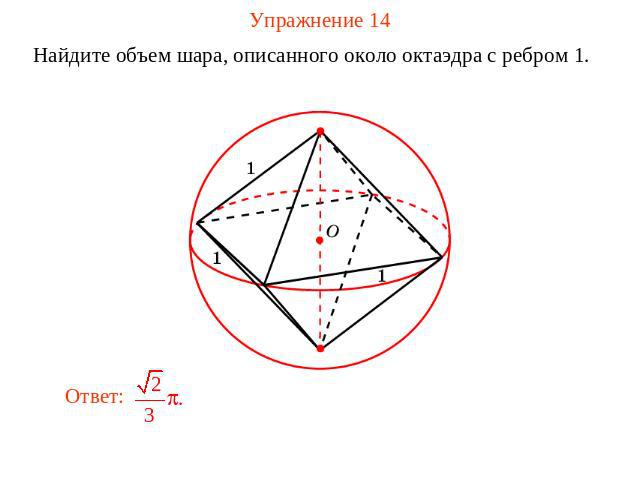
Упражнение 14 Найдите объем шара, описанного около октаэдра с ребром 1.

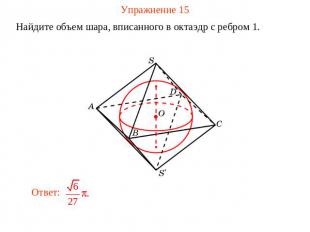
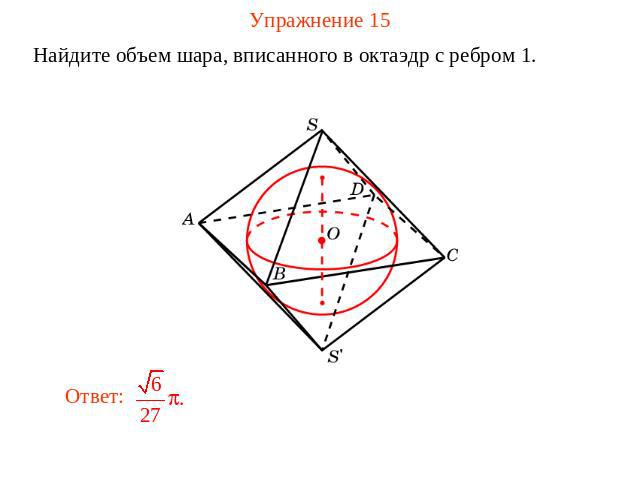
Упражнение 15 Найдите объем шара, вписанного в октаэдр с ребром 1.

Упражнение 16 Найдите объем шара, вписанного в цилиндр, радиус основания которого равен 1.

Упражнение 17 Найдите объем шара, описанного около цилиндра, радиус основания которого равен 3, а высота равна 8.

Упражнение 18 В конус, радиус основания которого равен 1, а образующая равна 2, вписан шар. Найдите его объем.

Упражнение 19 Около конуса, радиус основания которого равен 1, а образующая равна 2, описан шар. Найдите его объем.

Упражнение 20 В усеченный конус, радиусы оснований которого равны 2 и 1, вписан шар. Найдите его объем.

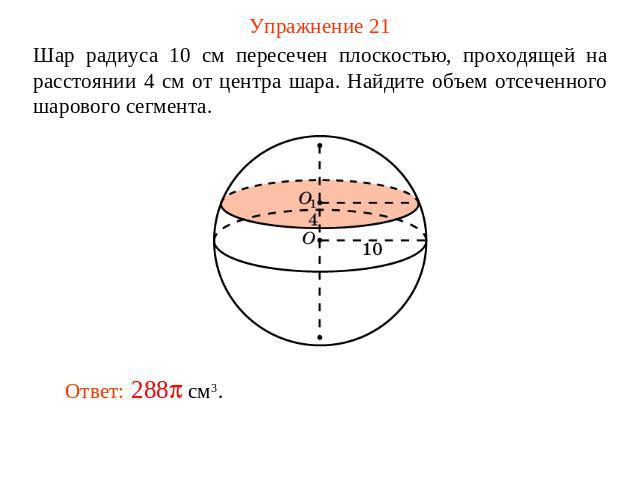
Упражнение 21 Шар радиуса 10 см пересечен плоскостью, проходящей на расстоянии 4 см от центра шара. Найдите объем отсеченного шарового сегмента.

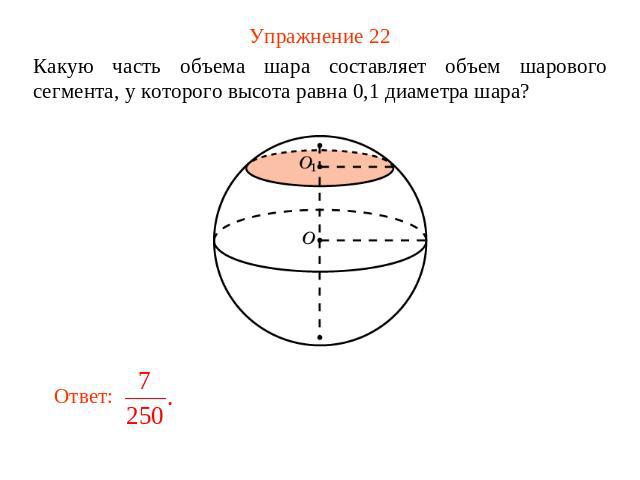
Упражнение 22 Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара?

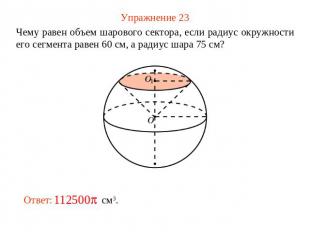
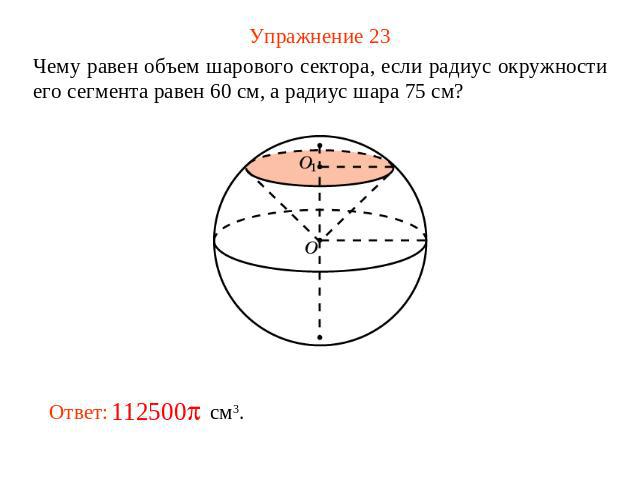
Упражнение 23 Чему равен объем шарового сектора, если радиус окружности его сегмента равен 60 см, а радиус шара 75 см?

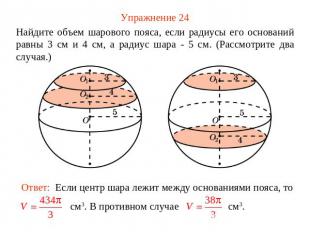
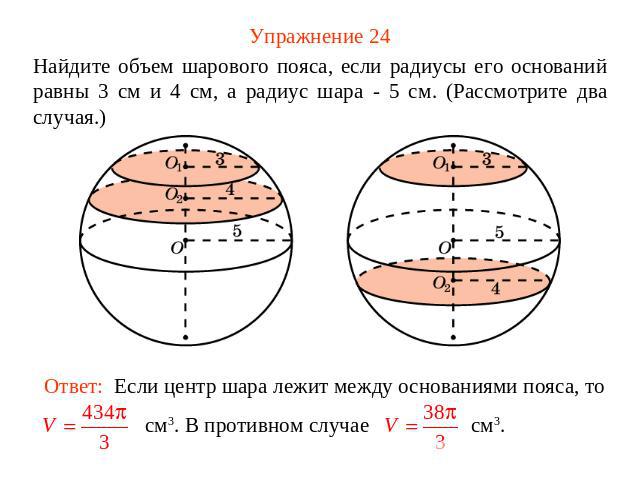
Упражнение 24 Найдите объем шарового пояса, если радиусы его оснований равны 3 см и 4 см, а радиус шара - 5 см. (Рассмотрите два случая.)Ответ: Если центр шара лежит между основаниями пояса, то см3. В противном случае см3.

Упражнение 25 Шар касается всех двенадцати ребер единичного куба. Найдите объем части шара, заключенной внутри этого куба.Решение: Часть шара, заключенная внутри куба, получается отсечением от шара радиуса шести шаровых сегментов высоты Объем каждого такого сегмента равенОбъем части шара, содержащейся в кубе, равен