Презентация на тему: Объем конуса

Объем конуса Решение задач

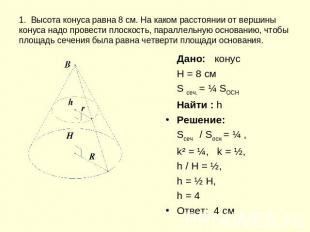
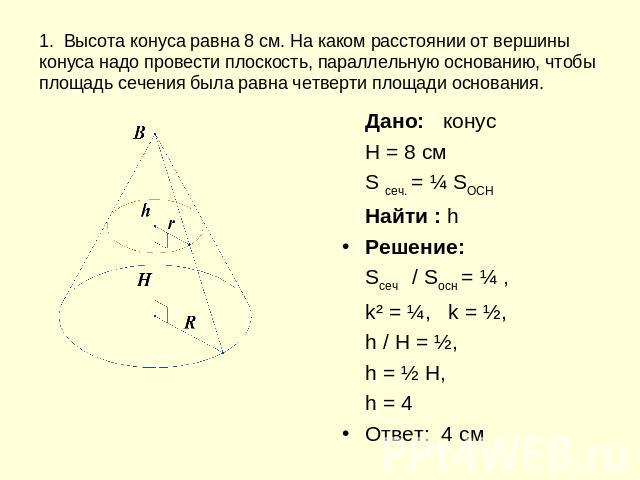
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна четверти площади основания. Дано: конусH = 8 см S сеч. = ¼ SOCHНайти : hРешение:Sсеч / Sосн = ¼ , k² = ¼, k = ½,h / H = ½, h = ½ Н, h = 4Ответ: 4 см

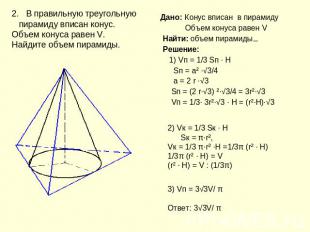
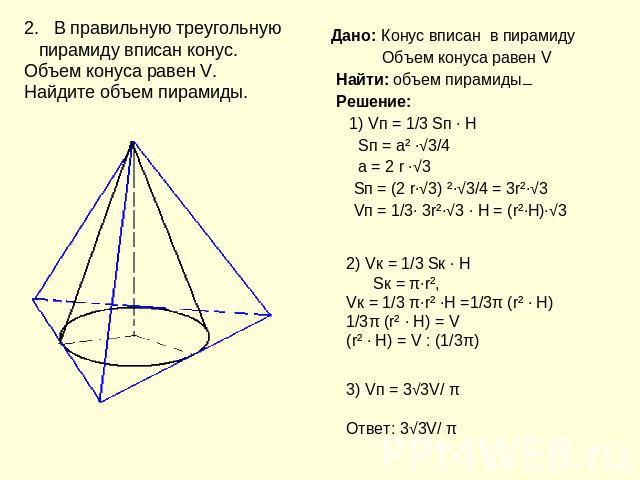
2. В правильную треугольную пирамиду вписан конус. Объем конуса равен V. Найдите объем пирамиды. Дано: Конус вписан в пирамиду Объем конуса равен V Найти: объем пирамиды Решение: 1) Vп = 1/3 Sп ∙ H Sп = а² ∙√3/4 а = 2 r ∙√3 Sп = (2 r∙√3) ²∙√3/4 = 3r²∙√3 Vп = 1/3∙ 3r²∙√3 ∙ H = (r²∙H)∙√3 2) Vк = 1/3 Sк ∙ H Sк = π∙r², Vк = 1/3 π∙r² ∙H =1/3π (r² ∙ Н)1/3π (r² ∙ Н) = V(r² ∙ Н) = V : (1/3π)

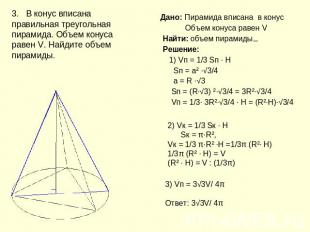
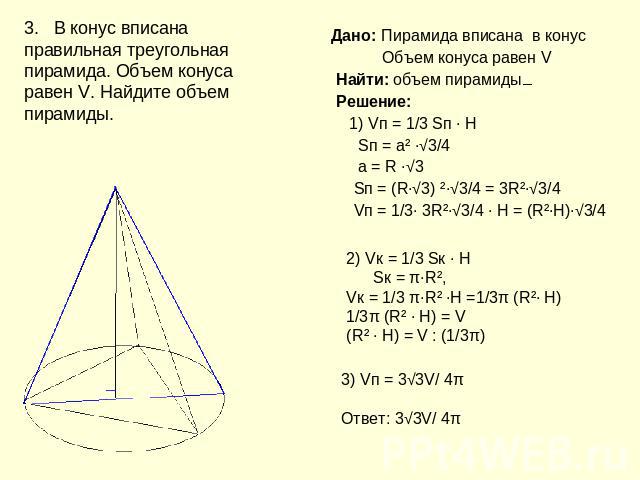
3. В конус вписана правильная треугольная пирамида. Объем конуса равен V. Найдите объем пирамиды. Дано: Пирамида вписана в конус Объем конуса равен V Найти: объем пирамиды Решение: 1) Vп = 1/3 Sп ∙ H Sп = а² ∙√3/4 а = R ∙√3 Sп = (R∙√3) ²∙√3/4 = 3R²∙√3/4 Vп = 1/3∙ 3R²∙√3/4 ∙ H = (R²∙H)∙√3/4 2) Vк = 1/3 Sк ∙ H Sк = π∙R², Vк = 1/3 π∙R² ∙H =1/3π (R²∙ Н)1/3π (R² ∙ Н) = V(R² ∙ Н) = V : (1/3π)