Презентация на тему: Объем конуса

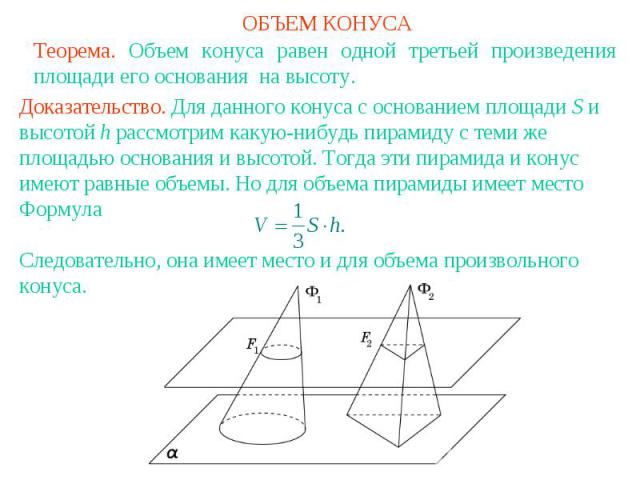
ОБЪЕМ КОНУСА Теорема. Объем конуса равен одной третьей произведения площади его основания на высоту.Доказательство. Для данного конуса с основанием площади S и высотой h рассмотрим какую-нибудь пирамиду с теми же площадью основания и высотой. Тогда эти пирамида и конус имеют равные объемы. Но для объема пирамиды имеет место Формула Следовательно, она имеет место и для объема произвольного конуса.
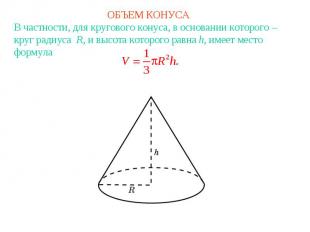
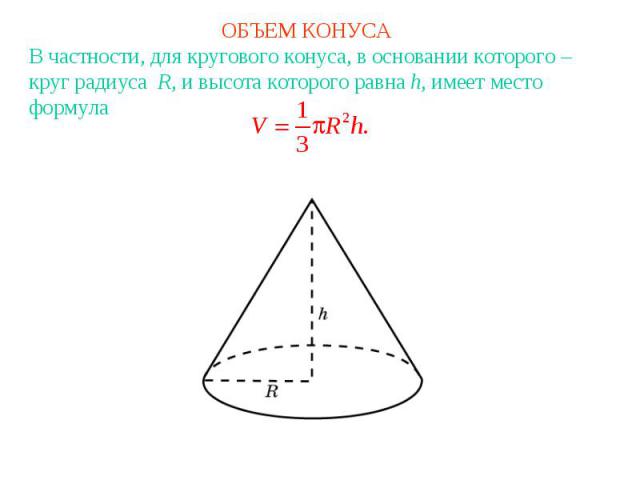
ОБЪЕМ КОНУСАВ частности, для кругового конуса, в основании которого – круг радиуса R, и высота которого равна h, имеет место формула

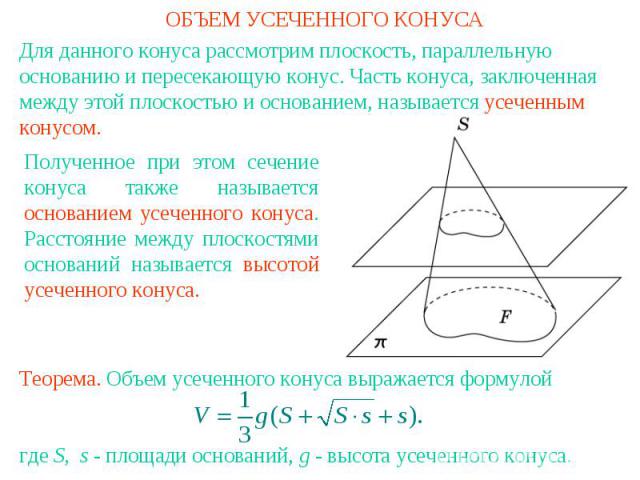
ОБЪЕМ УСЕЧЕННОГО КОНУСАДля данного конуса рассмотрим плоскость, параллельную основанию и пересекающую конус. Часть конуса, заключенная между этой плоскостью и основанием, называется усеченным конусом. Полученное при этом сечение конуса также называется основанием усеченного конуса. Расстояние между плоскостями оснований называется высотой усеченного конуса.Теорема. Объем усеченного конуса выражается формулойгде S, s - площади оснований, g - высота усеченного конуса.

ОБЪЕМ УСЕЧЕННОГО КОНУСАОбъем усеченного конуса, основания которого – круги радиусов R и r, а высота равна h, выражается формулой

Упражнение 1Во сколько раз увеличится объем кругового конуса, если: а) высоту увеличить в 3 раза; б) радиус основания увеличить в 2 раза?

Упражнение 2Изменится ли объем кругового конуса, если радиус основания увеличить в 2 раза, а высоту уменьшить в 2 раза?

Упражнение 3Цилиндр и конус имеют общее основание и высоту. Вычислите объем цилиндра, если объем конуса равен 40 π см3.
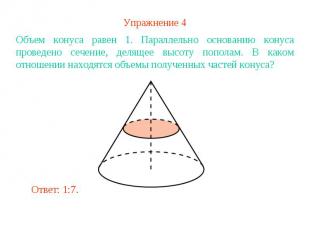
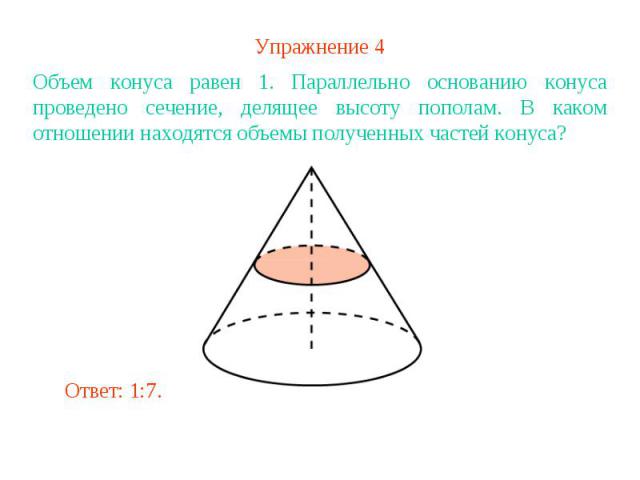
Упражнение 4Объем конуса равен 1. Параллельно основанию конуса проведено сечение, делящее высоту пополам. В каком отношении находятся объемы полученных частей конуса?
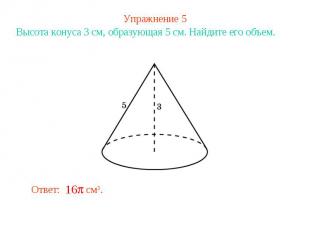
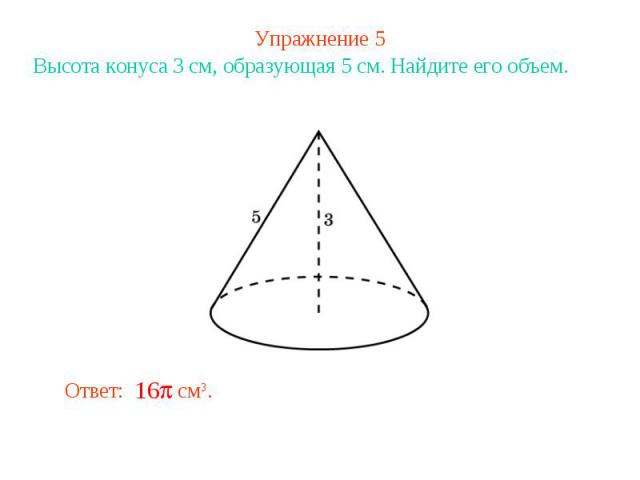
Упражнение 5Высота конуса 3 см, образующая 5 см. Найдите его объем.
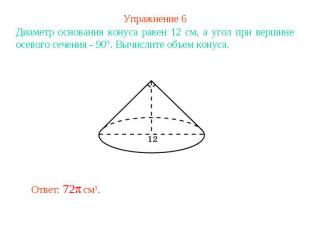
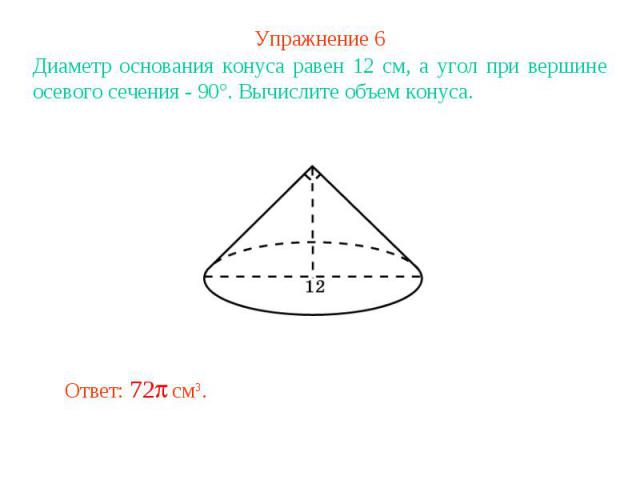
Упражнение 6Диаметр основания конуса равен 12 см, а угол при вершине осевого сечения - 90°. Вычислите объем конуса.
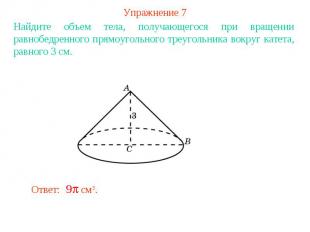
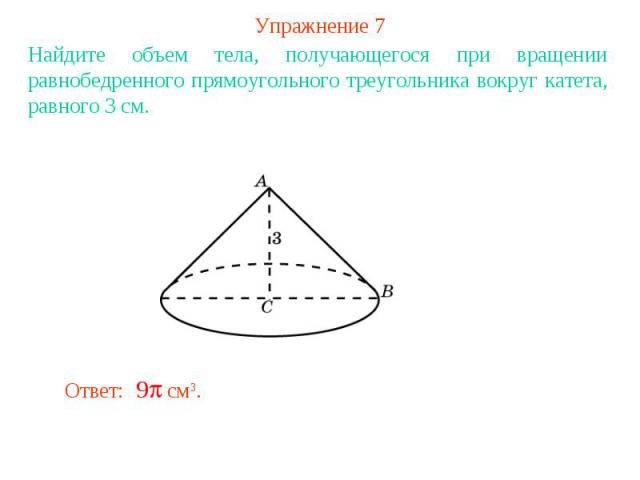
Упражнение 7Найдите объем тела, получающегося при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 3 см.
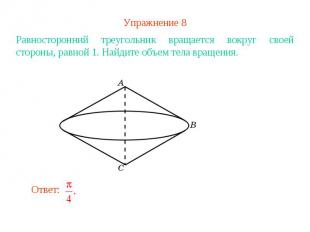
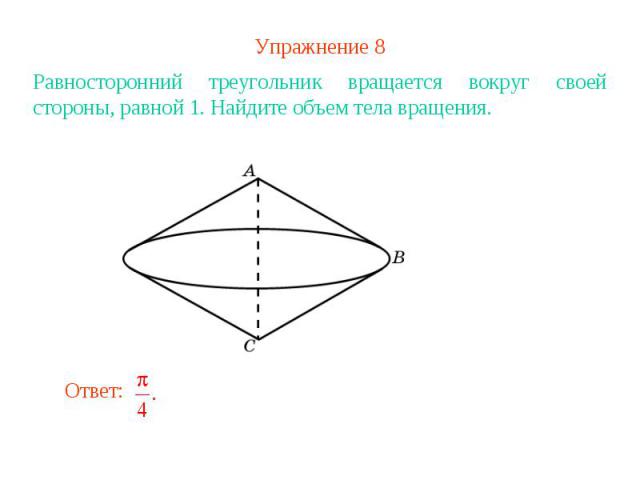
Упражнение 8Равносторонний треугольник вращается вокруг своей стороны, равной 1. Найдите объем тела вращения.

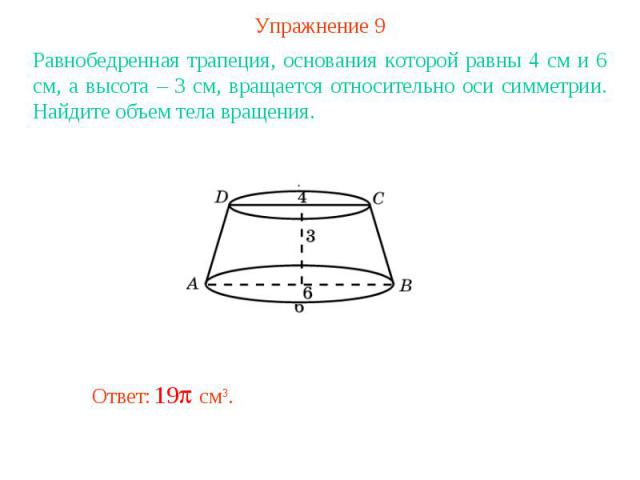
Упражнение 9Равнобедренная трапеция, основания которой равны 4 см и 6 см, а высота – 3 см, вращается относительно оси симметрии. Найдите объем тела вращения.
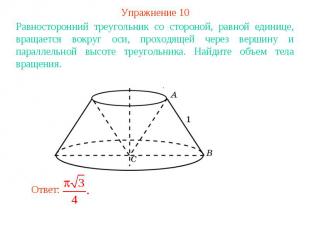
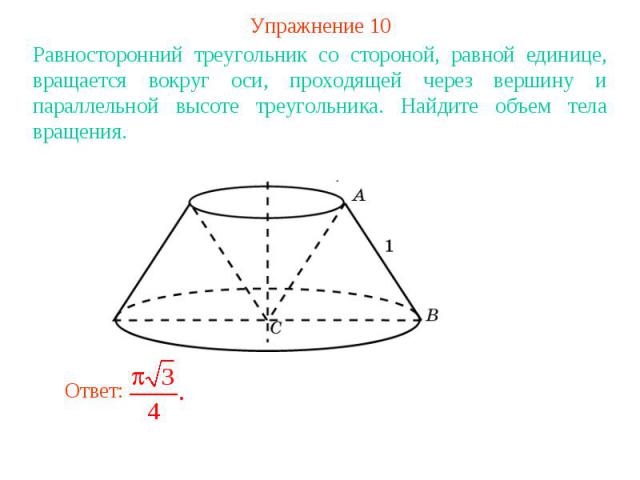
Упражнение 10Равносторонний треугольник со стороной, равной единице, вращается вокруг оси, проходящей через вершину и параллельной высоте треугольника. Найдите объем тела вращения.
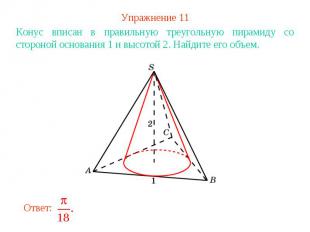
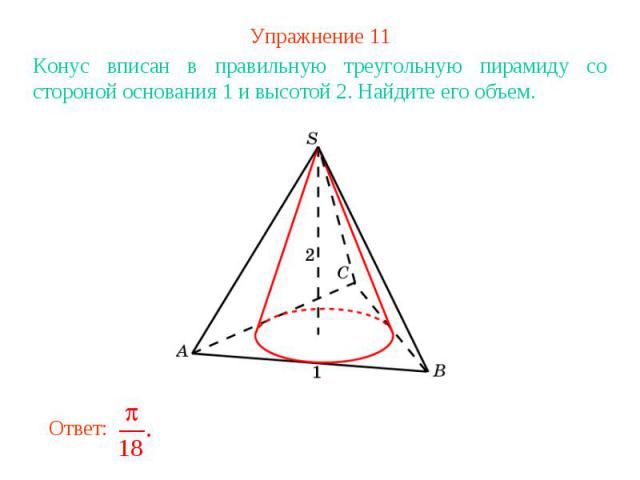
Упражнение 11Конус вписан в правильную треугольную пирамиду со стороной основания 1 и высотой 2. Найдите его объем.
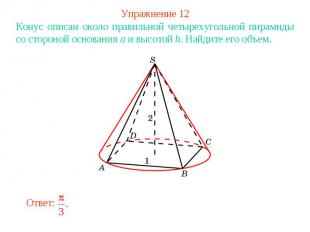
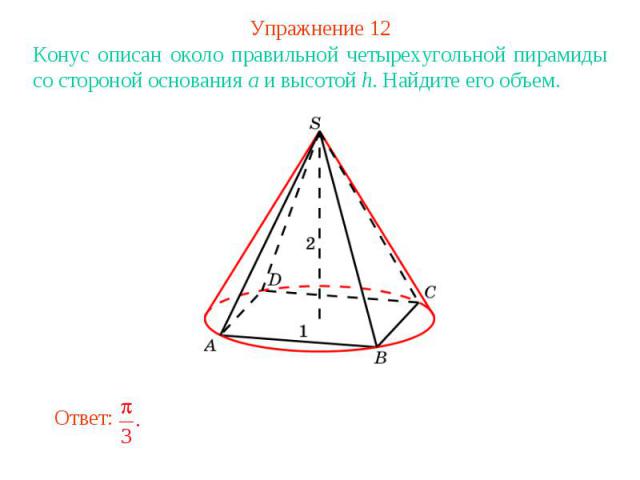
Упражнение 12Конус описан около правильной четырехугольной пирамиды со стороной основания a и высотой h. Найдите его объем.
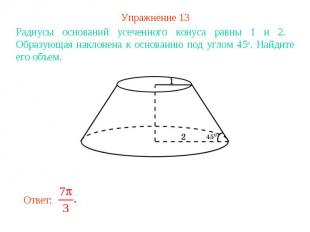
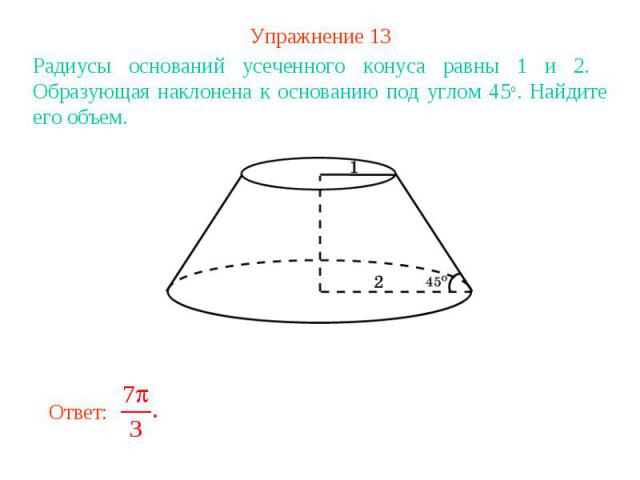
Упражнение 13Радиусы оснований усеченного конуса равны 1 и 2. Образующая наклонена к основанию под углом 45о. Найдите его объем.

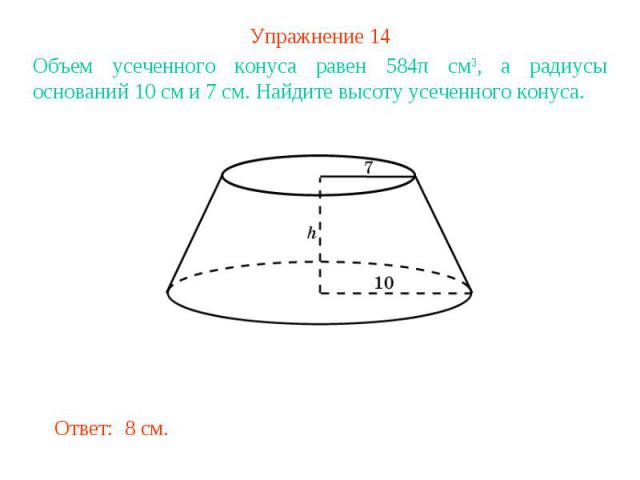
Упражнение 14Объем усеченного конуса равен 584π см3, а радиусы оснований 10 см и 7 см. Найдите высоту усеченного конуса.

Упражнение 15Усеченный конус, у которого радиусы оснований 3 см и 5 см, и полный конус такой же высоты равновелики. Чему равен радиус основания полного конуса?

Упражнение 16На меньшем основании усеченного конуса построен цилиндр, второе основание которого лежит в плоскости большего основания. Объем цилиндра составляет седьмую часть объема усеченного конуса. Найдите зависимость между радиусами оснований усеченного конуса.

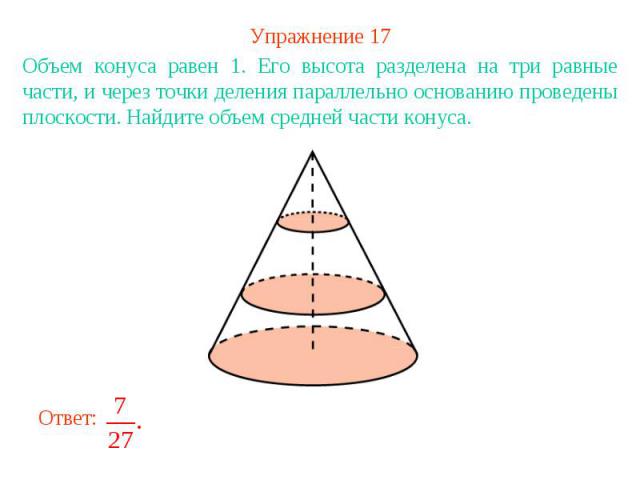
Упражнение 17Объем конуса равен 1. Его высота разделена на три равные части, и через точки деления параллельно основанию проведены плоскости. Найдите объем средней части конуса.

Упражнение 18Высота усеченного конуса равна 3. Радиус одного основания вдвое большее другого, а образующая наклонена к основанию под углом 45°. Найдите объем.
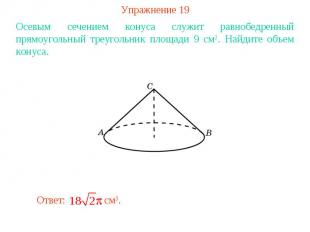
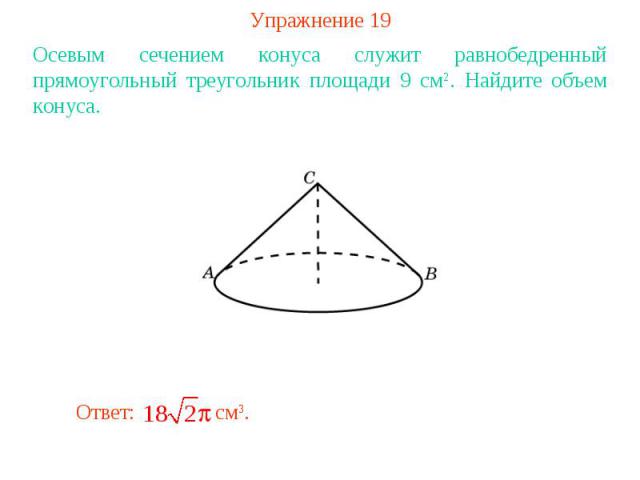
Упражнение 19Осевым сечением конуса служит равнобедренный прямоугольный треугольник площади 9 см2. Найдите объем конуса.

Упражнение 20Радиусы оснований усеченного конуса равны 3 см и 5 см. Найдите отношение объемов частей усеченного конуса, на которые он делится средним сечением.
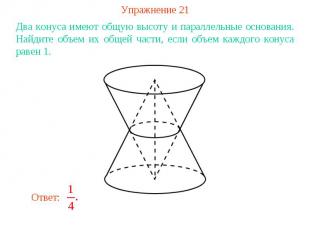
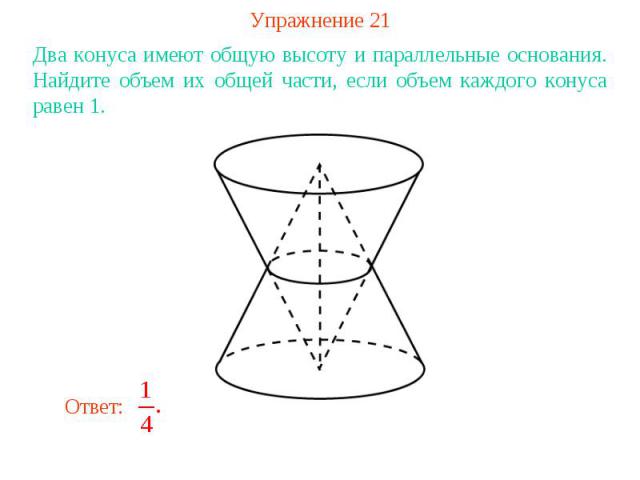
Упражнение 21Два конуса имеют общую высоту и параллельные основания. Найдите объем их общей части, если объем каждого конуса равен 1.

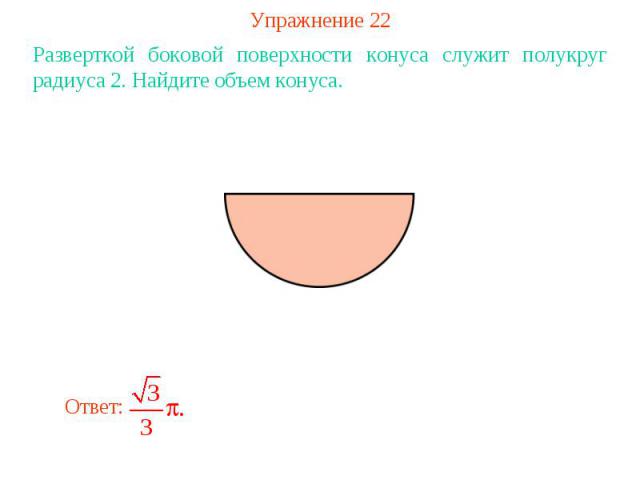
Упражнение 22Разверткой боковой поверхности конуса служит полукруг радиуса 2. Найдите объем конуса.

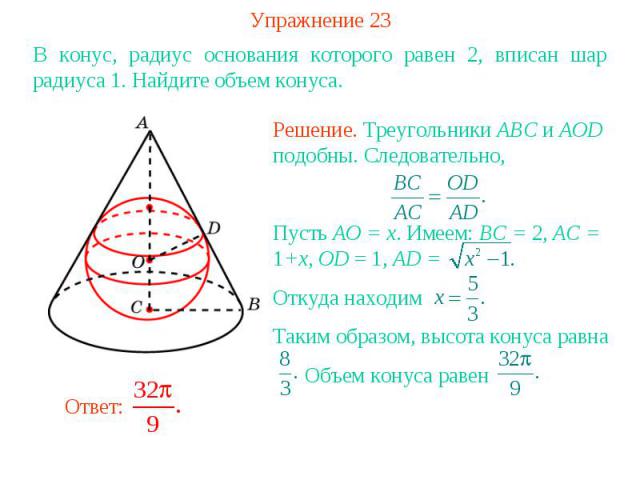
Упражнение 23В конус, радиус основания которого равен 2, вписан шар радиуса 1. Найдите объем конуса.Решение. Треугольники ABC и AOD подобны. Следовательно, Пусть AO = x. Имеем: BC = 2, AC = 1+x, OD = 1, AD = Откуда находимТаким образом, высота конуса равна Объем конуса равен