Презентация на тему: Кристаллы

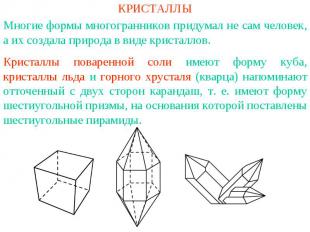
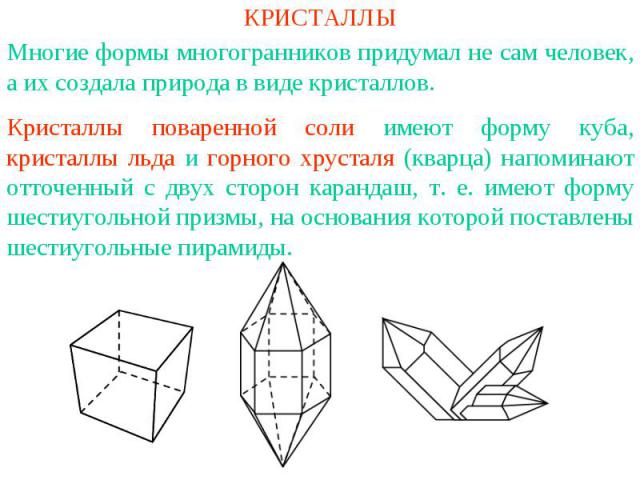
КРИСТАЛЛЫМногие формы многогранников придумал не сам человек, а их создала природа в виде кристаллов. Кристаллы поваренной соли имеют форму куба, кристаллы льда и горного хрусталя (кварца) напоминают отточенный с двух сторон карандаш, т. е. имеют форму шестиугольной призмы, на основания которой поставлены шестиугольные пирамиды.

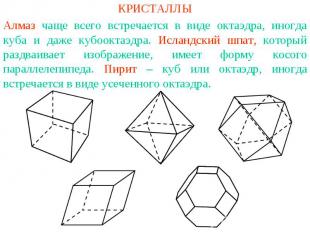
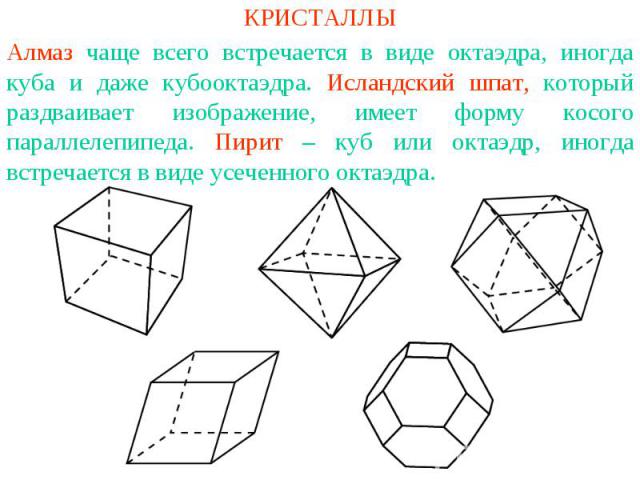
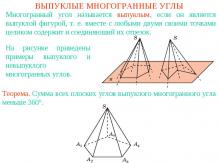
КРИСТАЛЛЫАлмаз чаще всего встречается в виде октаэдра, иногда куба и даже кубооктаэдра. Исландский шпат, который раздваивает изображение, имеет форму косого параллелепипеда. Пирит – куб или октаэдр, иногда встречается в виде усеченного октаэдра.

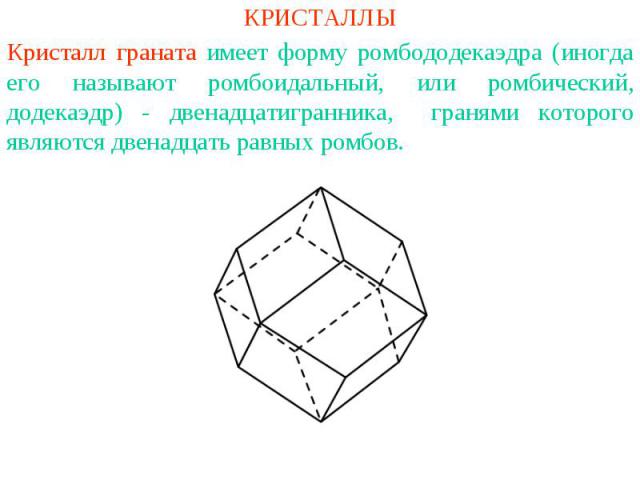
КРИСТАЛЛЫКристалл граната имеет форму ромбододекаэдра (иногда его называют ромбоидальный, или ромбический, додекаэдр) - двенадцатигранника, гранями которого являются двенадцать равных ромбов.

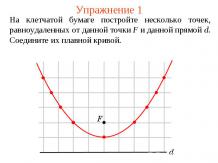
Упражнение 1Возьмем два одинаковых куба. Разобьем один из них на шесть одинаковых четырехугольных пирамид с вершинами в центре куба и основаниями - гранями куба. Приложим теперь эти пирамиды к граням второго куба так, чтобы основания пирамид совместились с гранями куба. Покажите, что образовавшийся при этом многогранник будет ромбододекаэдром.

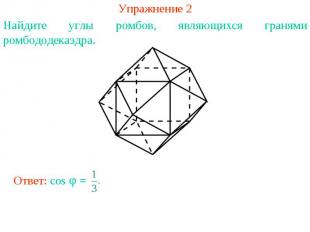
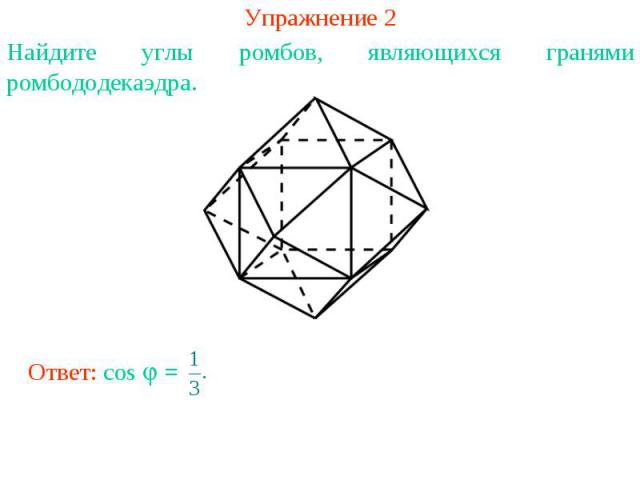
Упражнение 2Найдите углы ромбов, являющихся гранями ромбододекаэдра.

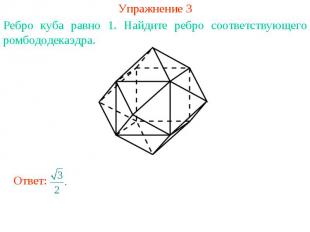
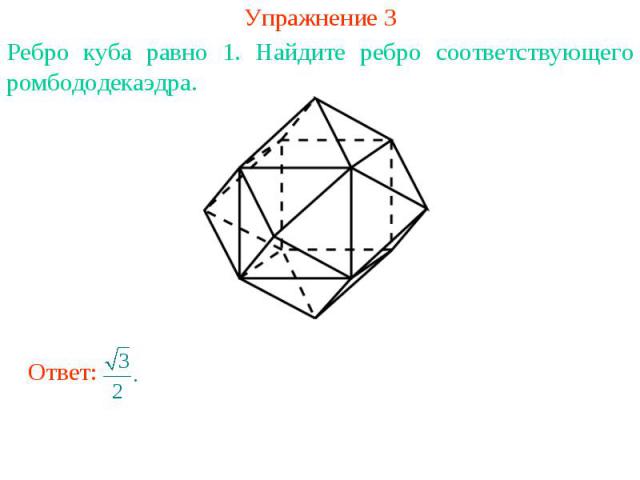
Упражнение 3Ребро куба равно 1. Найдите ребро соответствующего ромбододекаэдра.

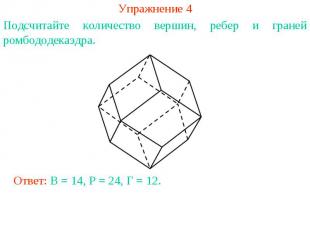
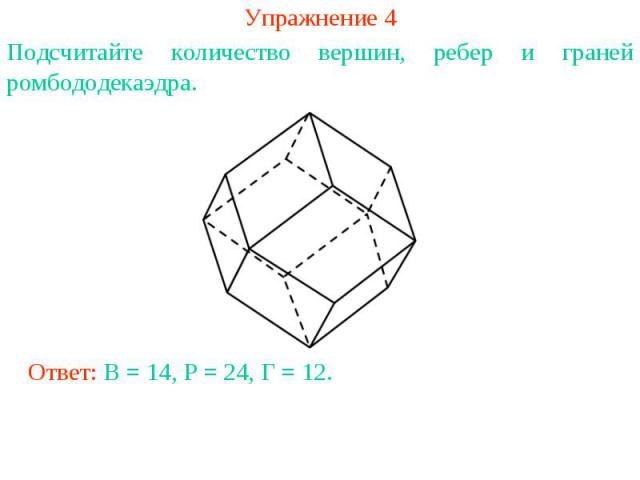
Упражнение 4Подсчитайте количество вершин, ребер и граней ромбододекаэдра.

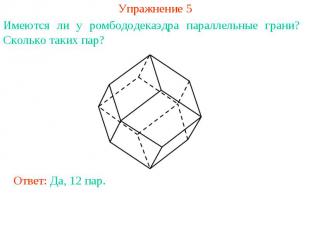
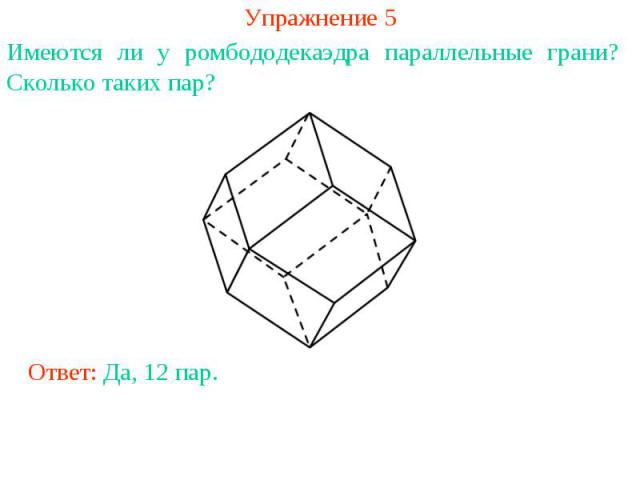
Упражнение 5Имеются ли у ромбододекаэдра параллельные грани? Сколько таких пар?

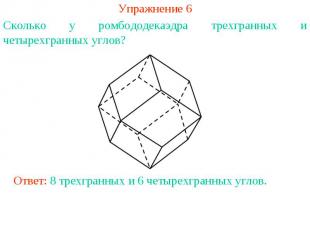
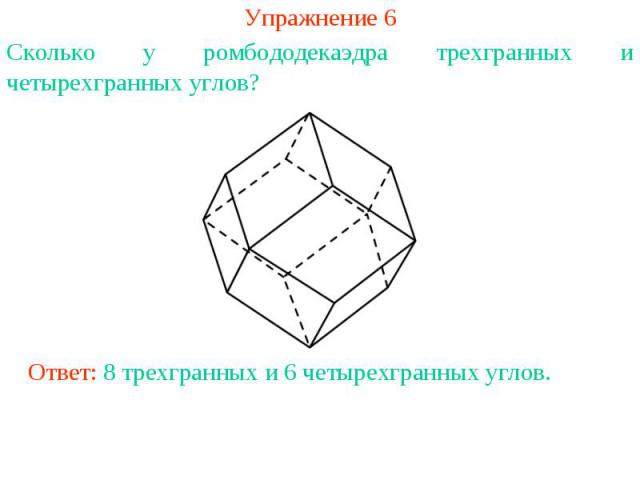
Упражнение 6Сколько у ромбододекаэдра трехгранных и четырехгранных углов?Ответ: 8 трехгранных и 6 четырехгранных углов.

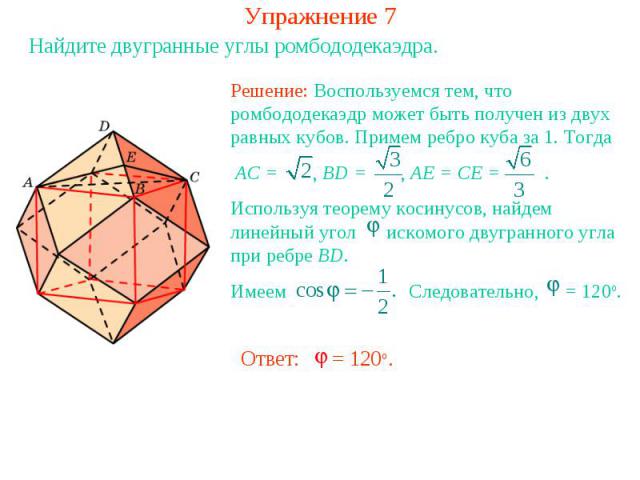
Упражнение 7Найдите двугранные углы ромбододекаэдра.Решение: Воспользуемся тем, что ромбододекаэдр может быть получен из двух равных кубов. Примем ребро куба за 1. Тогда AC = , BD = , AE = CE = . Используя теорему косинусов, найдем линейный угол искомого двугранного угла при ребре BD. Имеем Следовательно, = 120о.

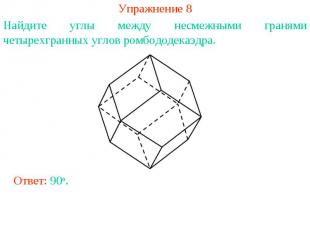
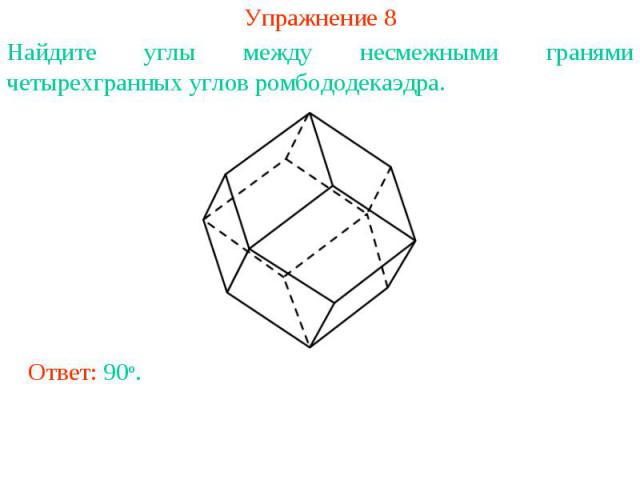
Упражнение 8Найдите углы между несмежными гранями четырехгранных углов ромбододекаэдра.

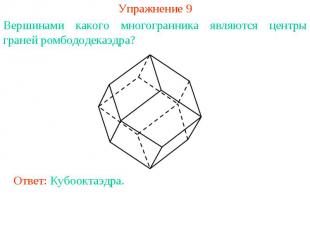
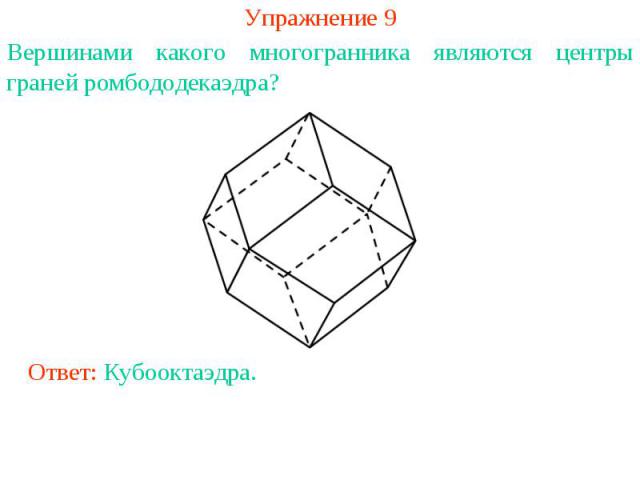
Упражнение 9Вершинами какого многогранника являются центры граней ромбододекаэдра?Ответ: Кубооктаэдра.

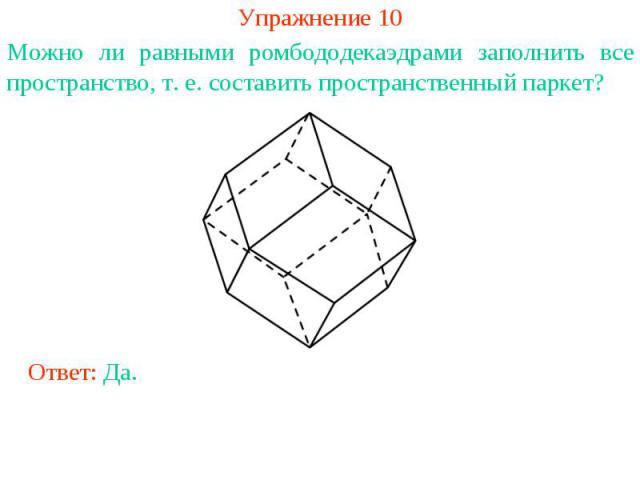
Упражнение 10Можно ли равными ромбододекаэдрами заполнить все пространство, т. е. составить пространственный паркет?

Упражнение 11Найдите трехгранные и четырехгранные углы ромбододекаэдра – многогранника, поверхность которого состоит из двенадцати ромбов.Заметим, что равными ромбододекаэдрами можно заполнить все пространство (составить пространственный паркет). Для этого сначала заполним пространство равными кубами, закрашенными в черный и белый цвета в шахматном порядке. Затем белые кубы разобьем на правильные четырехугольные пирамиды и присоединим их к черным кубам. Получим искомое заполнение пространства ромбододекаэдрами. При этом в каждой вершине сходится или шесть равных четырехгранных углов, или четыре равных трехгранных углов ромбододекаэдров. Таким образом, величина четырехгранного угла ромбододекаэдра равна 60о, а величина трехгранного угла ромбододекаэдра равна 90о.

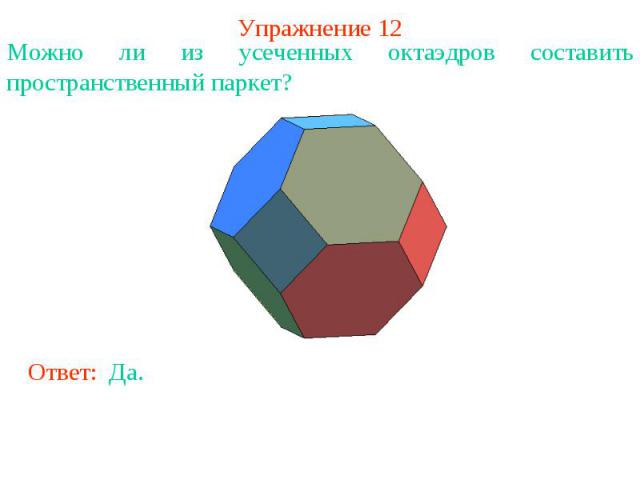
Упражнение 12Можно ли из усеченных октаэдров составить пространственный паркет?

Фотографии кристаллов можно посмотреть на сайте минералогического музея им. А.Е. Ферсмана в Москве, www.fmm.ru