Презентация на тему: Расстояние от точки до прямой и плоскости
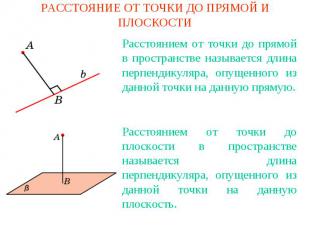
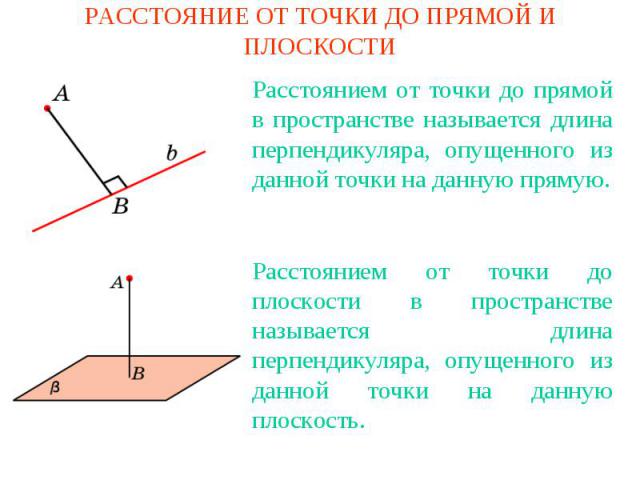
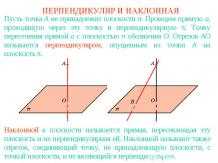
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ И ПЛОСКОСТИРасстоянием от точки до прямой в пространстве называется длина перпендикуляра, опущенного из данной точки на данную прямую.Расстоянием от точки до плоскости в пространстве называется длина перпендикуляра, опущенного из данной точки на данную плоскость.
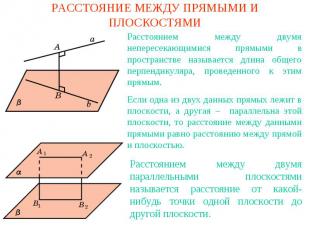
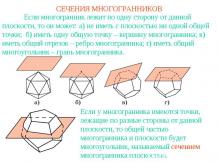
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИРасстоянием между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым. Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.Расстоянием между двумя параллельными плоскостями называется расстояние от какой-нибудь точки одной плоскости до другой плоскости.

Упражнение 1Из точки А, не принадлежащей плоскости α, проведена наклонная к этой плоскости. Определите угол между этой наклонной и плоскостью α, если расстояние от точки А до плоскости α: а) равно ортогональной проекции наклонной; б) в два раза меньше самой наклонной.

Упражнение 2В кубе А...D1 с ребром а найдите расстояние между вершиной А1 и: а) ребром CD; б) диагональю BD; в) диагональю АС1.

Упражнение 3Чему равно расстояние между параллельными гранями в кубе?

Упражнение 4В кубе A...D1 с ребром а найдите расстояние: а) от вершины А1 до плоскости грани ABCD; б) от вершины А до плоскости грани BB1D1D; в) от вершины А1 до плоскости AB1D1.
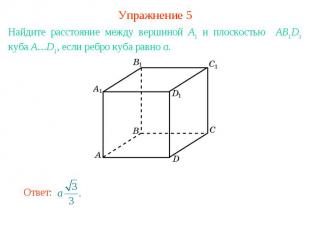
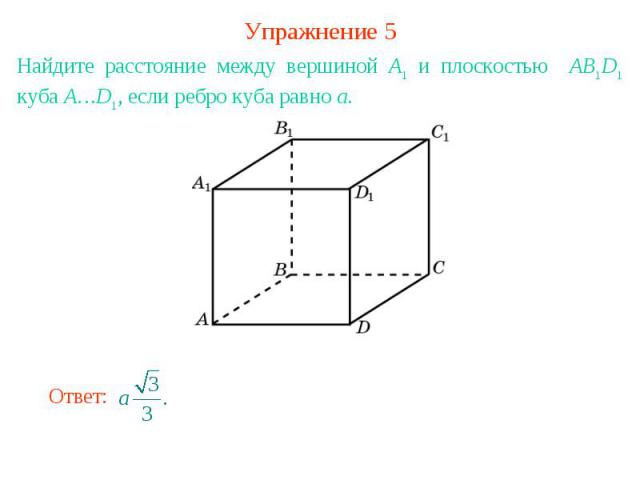
Упражнение 5Найдите расстояние между вершиной A1 и плоскостью AB1D1 куба A…D1, если ребро куба равно a.

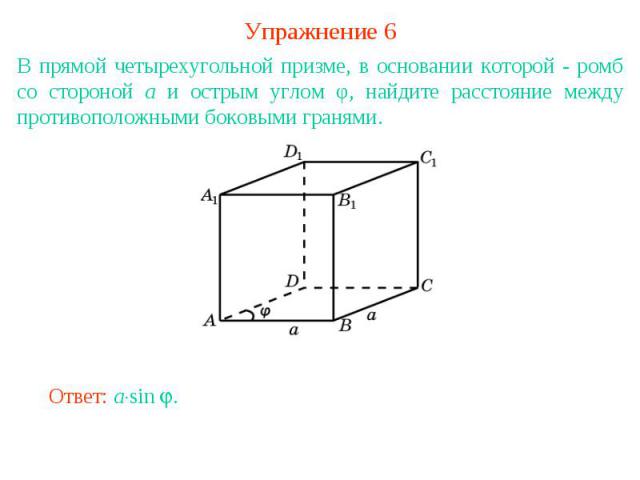
Упражнение 6В прямой четырехугольной призме, в основании которой - ромб со стороной а и острым углом φ, найдите расстояние между противоположными боковыми гранями.
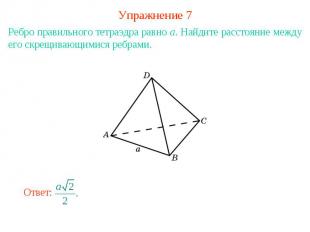
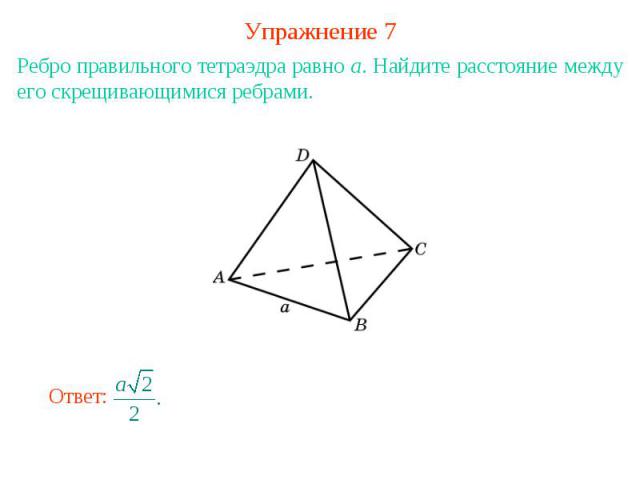
Упражнение 7Ребро правильного тетраэдра равно a. Найдите расстояние между его скрещивающимися ребрами.
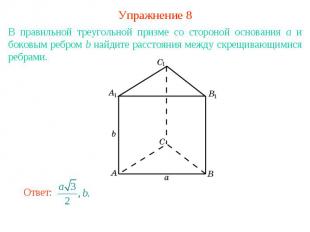
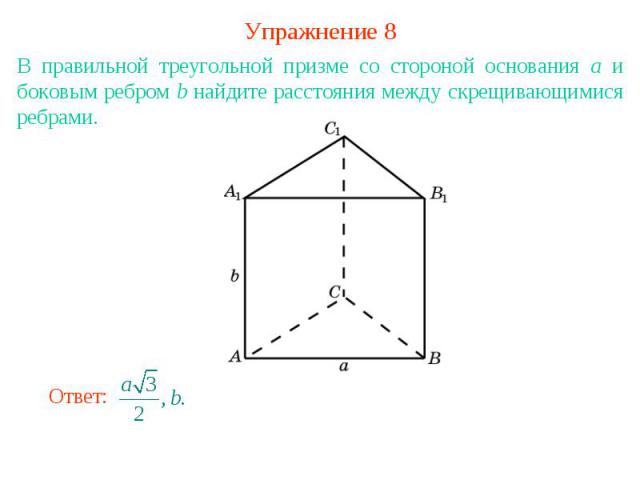
Упражнение 8В правильной треугольной призме со стороной основания а и боковым ребром b найдите расстояния между скрещивающимися ребрами.

Упражнение 9Для куба A...D1 с ребром а найдите расстояние между скрещивающимися прямыми: а) AD и A1C1; б) AC1 и DD1; в) AD и A1B1; г) AC и B1D1; д) AC и DD1; е) AC1 и BD.

Упражнение 10Найдите геометрическое место точек пространства, равноудаленных от двух параллельных прямых.

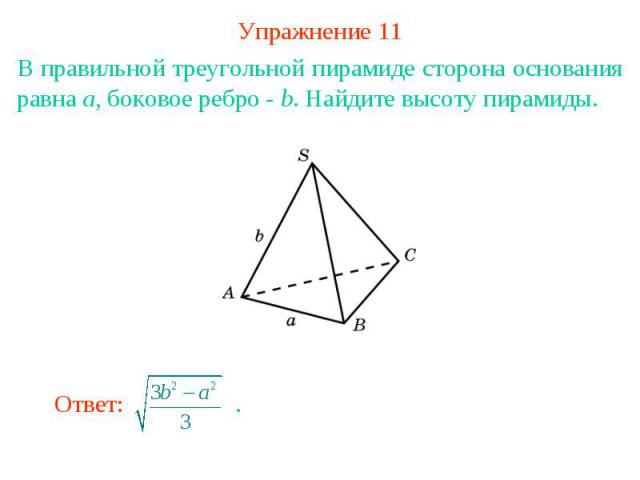
Упражнение 11В правильной треугольной пирамиде сторона основания равна a, боковое ребро - b. Найдите высоту пирамиды.

Упражнение 12В правильной четырехугольной пирамиде сторона основания равна а, высота - h. Найдите боковое ребро пирамиды.

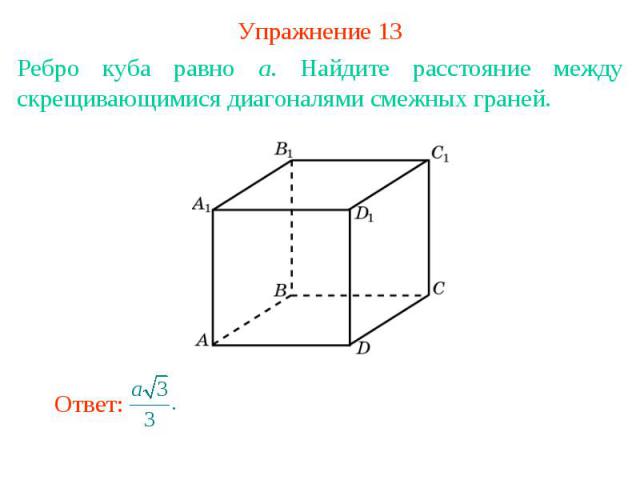
Упражнение 13Ребро куба равно a. Найдите расстояние между скрещивающимися диагоналями смежных граней.
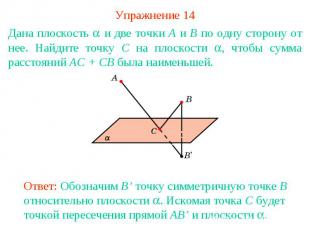
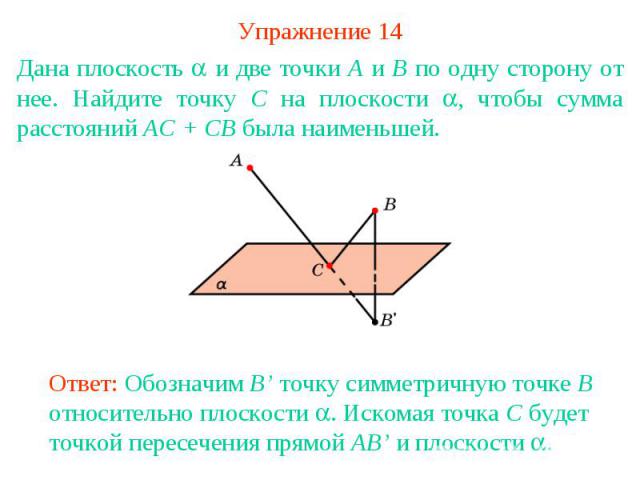
Упражнение 14Дана плоскость и две точки A и B по одну сторону от нее. Найдите точку C на плоскости , чтобы сумма расстояний AC + CB была наименьшей.Ответ: Обозначим B’ точку симметричную точке B относительно плоскости . Искомая точка C будет точкой пересечения прямой AB’ и плоскости .