Презентация на тему: Прямоугольные треугольники

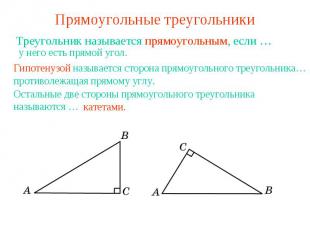
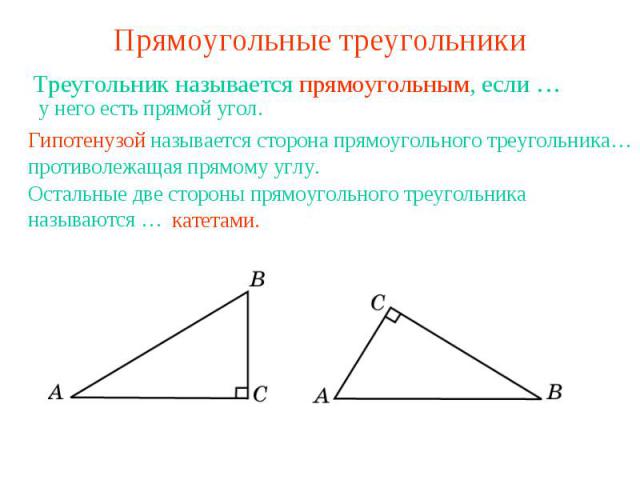
Прямоугольные треугольники Треугольник называется прямоугольным, если …у него есть прямой угол.Гипотенузой называется сторона прямоугольного треугольника…противолежащая прямому углу.Остальные две стороны прямоугольного треугольника называются …

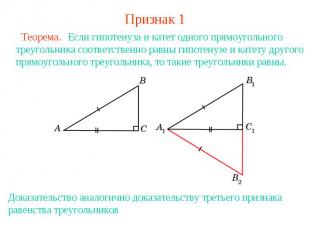
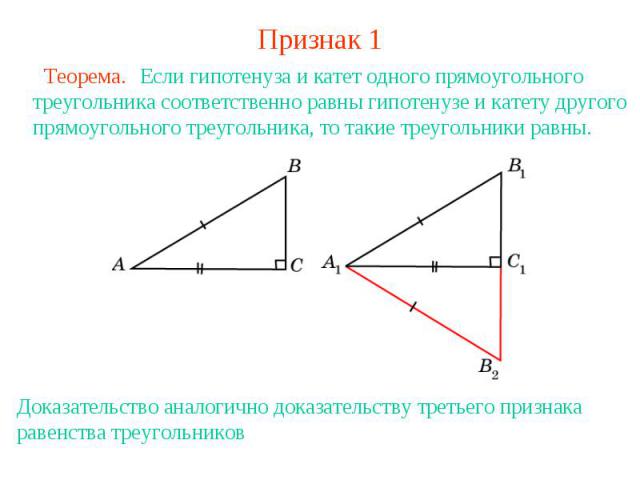
Признак 1 Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.Доказательство аналогично доказательству третьего признака равенства треугольников

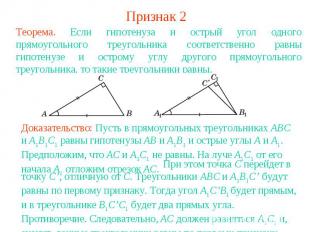
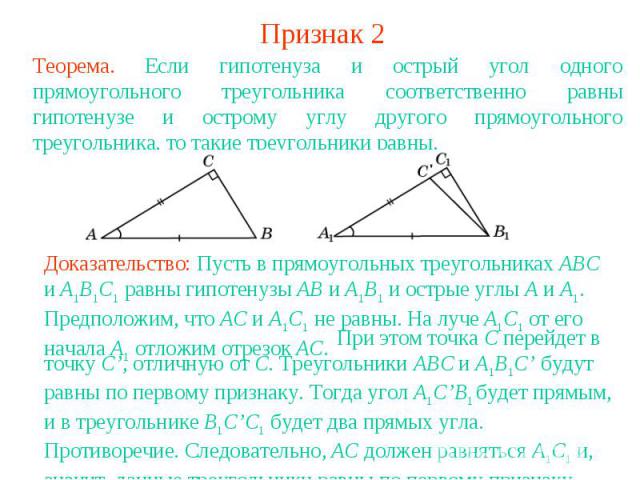
Признак 2Теорема. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.Доказательство: Пусть в прямоугольных треугольниках ABC и A1B1C1 равны гипотенузы AB и A1B1 и острые углы A и A1. Предположим, что AC и A1C1 не равны. На луче A1C1 от его начала A1 отложим отрезок AC. При этом точка C перейдет в точку C’, отличную от C. Треугольники ABC и A1B1C’ будут равны по первому признаку. Тогда угол A1C’B1 будет прямым, и в треугольнике B1C’C1 будет два прямых угла. Противоречие. Следовательно, AC должен равняться A1C1 и, значит, данные треугольники равны по первому признаку.

Вопрос 1Какой треугольник называется прямоугольным? Ответ: Прямоугольным называется треугольник, у которого есть прямой угол.

Вопрос 2Что называется гипотенузой прямоугольного треугольника?Ответ: Гипотенузой называется сторона прямоугольного треугольника, противолежащая прямому углу.

Вопрос 3Что называется катетами прямоугольного треугольника?Ответ: Катетами называются стороны прямоугольного треугольника, противолежащие острым углам.

Упражнение 1Что больше, катет или гипотенуза прямоугольного треугольника?Ответ: Гипотенуза.

Упражнение 2Может ли прямоугольный треугольник иметь стороны, равные 4, 5, 5?

Упражнение 3Может ли прямоугольный треугольник иметь катеты 11 см и 111 см?

Упражнение 4Может ли прямоугольный треугольник иметь тупой угол?

Упражнение 5Могут ли неравные прямоугольные треугольники иметь равные катеты?

Упражнение 6Может ли прямоугольный треугольник быть: а) равнобедренным; б) равносторонним?

Упражнение 7Стороны прямоугольного треугольника равны 3 см, 4 см, 5 см. Чему равна гипотенуза?

Упражнение 6Верно ли, что если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому другого прямоугольного треугольника, то такие треугольники равны.?

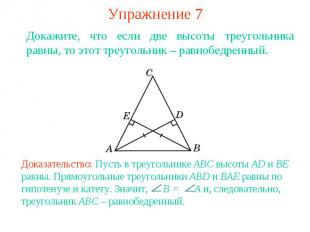
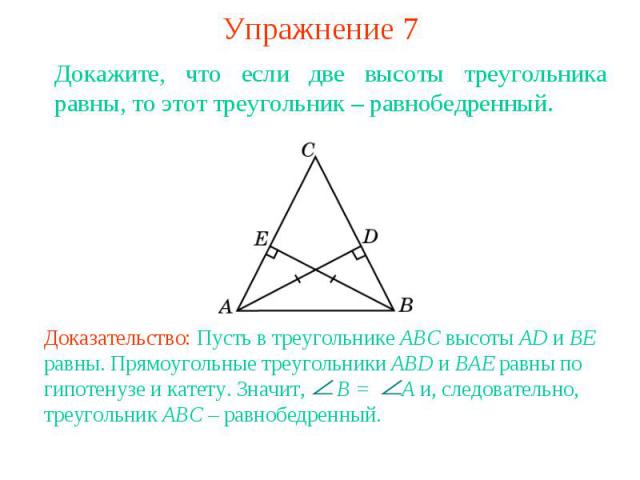
Упражнение 7Докажите, что если две высоты треугольника равны, то этот треугольник – равнобедренный. Доказательство: Пусть в треугольнике ABC высоты AD и BE равны. Прямоугольные треугольники ABD и BAE равны по гипотенузе и катету. Значит, B = A и, следовательно, треугольник ABC – равнобедренный.

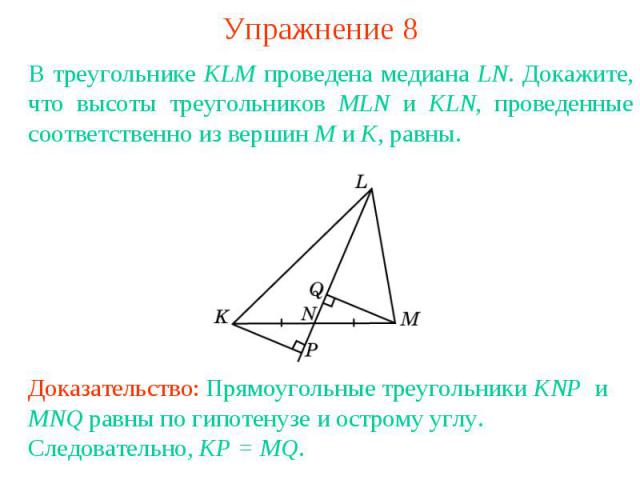
Упражнение 8В треугольнике KLM проведена медиана LN. Докажите, что высоты треугольников MLN и KLN, проведенные соответственно из вершин M и K, равны.Доказательство: Прямоугольные треугольники KNP и MNQ равны по гипотенузе и острому углу. Следовательно, KP = MQ.

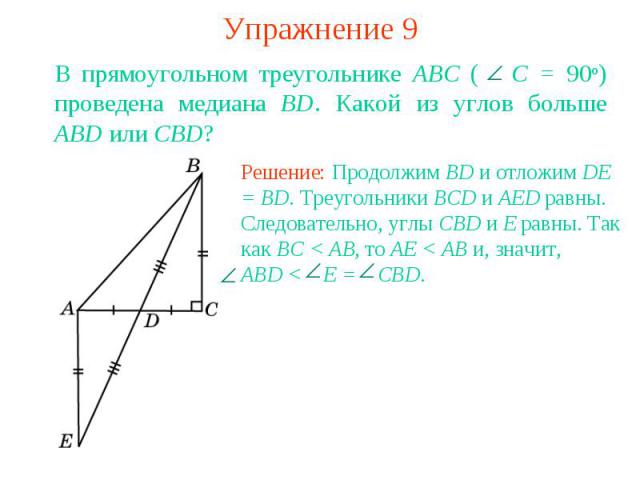
Упражнение 9В прямоугольном треугольнике ABC ( С = 90о) проведена медиана BD. Какой из углов больше ABD или CBD?Решение: Продолжим BD и отложим DE = BD. Треугольники BCD и AED равны. Следовательно, углы CBD и E равны. Так как BC < AB, то AE < AB и, значит, ABD < E = CBD.

Упражнение 10В прямоугольном треугольнике ABC ( С = 90о) проведена биссектриса BE. Какой из отрезков больше AE или CE?Решение: Отложим на стороне BA отрезок BF = BC. Треугольники BCE и BFE равны. Следовательно, CE = EF. Так как EF < AE, то CE < AE.

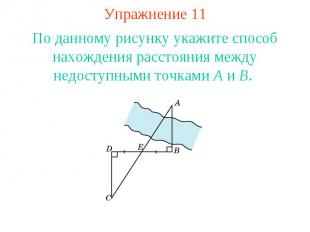
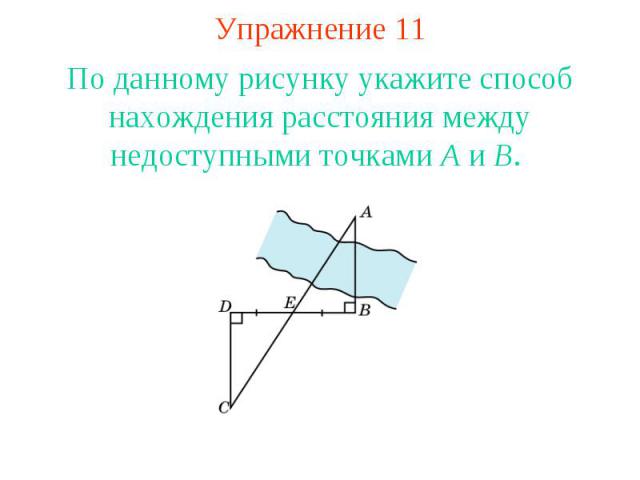
Упражнение 11По данному рисунку укажите способ нахождения расстояния между недоступными точками A и B.