Презентация на тему: Равнобедренные треугольники
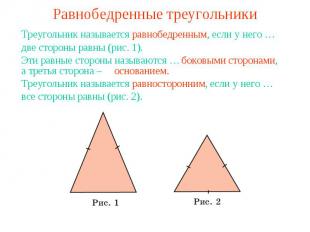
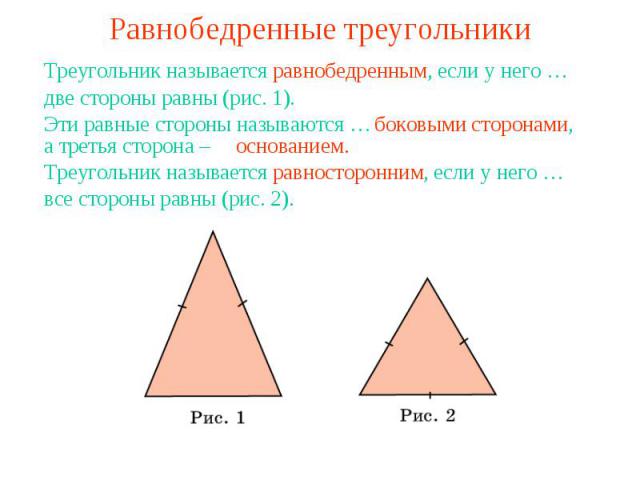
Равнобедренные треугольникиТреугольник называется равнобедренным, если у него …две стороны равны (рис. 1).Эти равные стороны называются …а третья сторона – Треугольник называется равносторонним, если у него …все стороны равны (рис. 2).

ТеоремаВ равнобедренном треугольнике биссектриса, проведенная к основанию, является одновременно медианой и высотой.Доказательство. Пусть ABC – равнобедренный треугольник, AC = BC, CD – биссектриса. Тогда треугольник ACD равен треугольнику BCD по первому признаку равенства треугольников (АС = ВС, СD – общая сторона, ACD = BCD). Следовательно, имеют место равенства AD = BD, ADC = BDC. Первое из этих равенств означает, что CD является медианой данного треугольника, второе – что CD является его высотой.

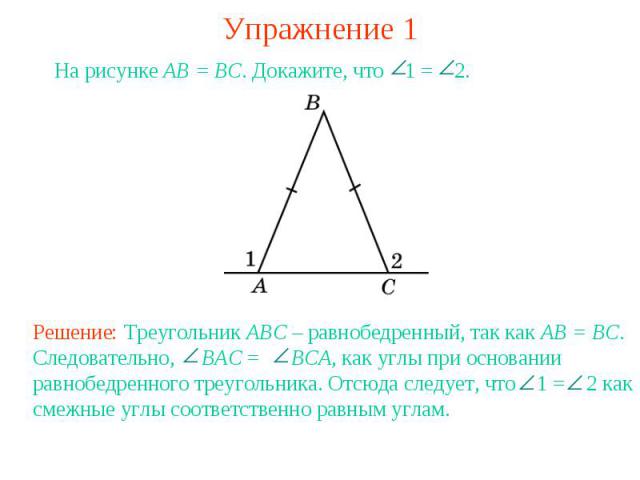
Упражнение 1На рисунке AB = BC. Докажите, что 1 = 2. Решение: Треугольник ABC – равнобедренный, так как AB = BC. Следовательно, BAC = BCA, как углы при основании равнобедренного треугольника. Отсюда следует, что 1 = 2 как смежные углы соответственно равным углам.
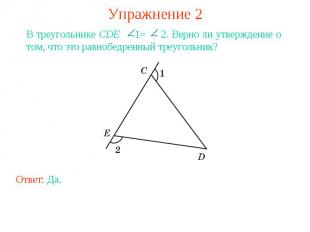
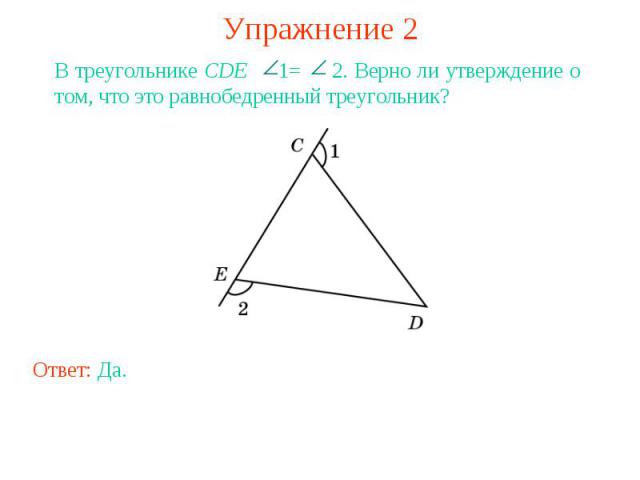
Упражнение 2В треугольнике CDE 1= 2. Верно ли утверждение о том, что это равнобедренный треугольник?
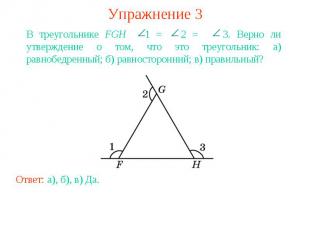
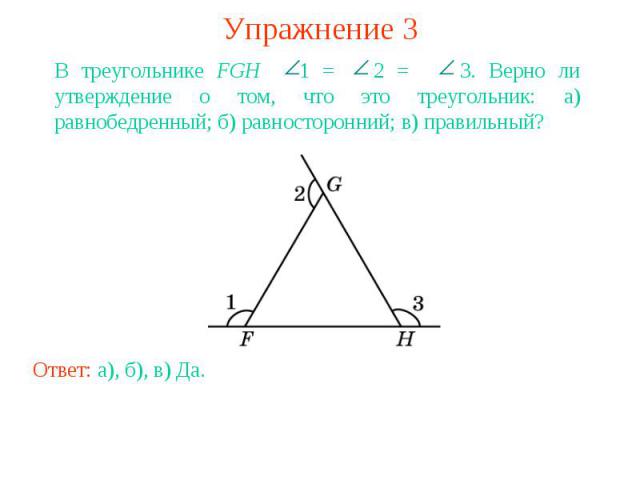
Упражнение 3В треугольнике FGH 1 = 2 = 3. Верно ли утверждение о том, что это треугольник: а) равнобедренный; б) равносторонний; в) правильный?

Упражнение 4Периметр равнобедренного треугольника равен 2 м, а основание - 0,4 м. Найдите боковую сторону.

Упражнение 5Периметр равнобедренного треугольника равен 7,5 м, а боковая сторона - 2 м. Найдите основание.

Упражнение 6Периметр равнобедренного треугольника равен 15,6 м. Найдите его стороны, если: а) основание меньше боковой стороны на 3 м; б) основание больше боковой стороны на 3 м.

Упражнение 7Основание и боковая сторона равнобедренного треугольника относятся как 3:8. Найдите стороны этого треугольника, если его периметр равен 38 см.

Упражнение 8В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Найдите ее длину, если периметр треугольника АВС равен 50 м, а треугольника АВD - 40 м.
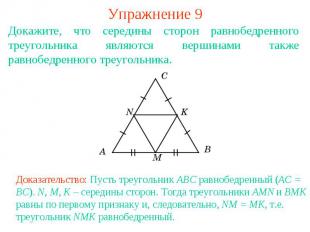
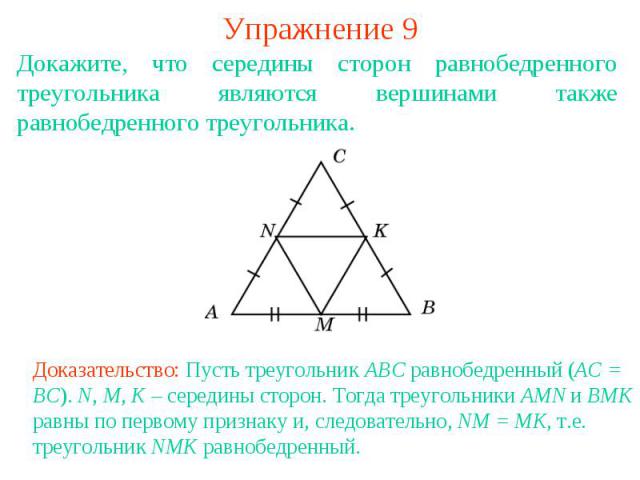
Упражнение 9Докажите, что середины сторон равнобедренного треугольника являются вершинами также равнобедренного треугольника.Доказательство: Пусть треугольник ABC равнобедренный (AC = BC). N, M, K – середины сторон. Тогда треугольники AMN и BMK равны по первому признаку и, следовательно, NM = MK, т.е. треугольник NMK равнобедренный.
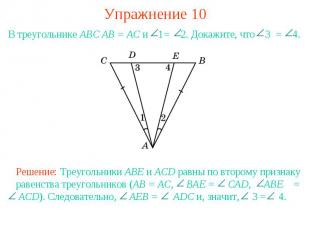
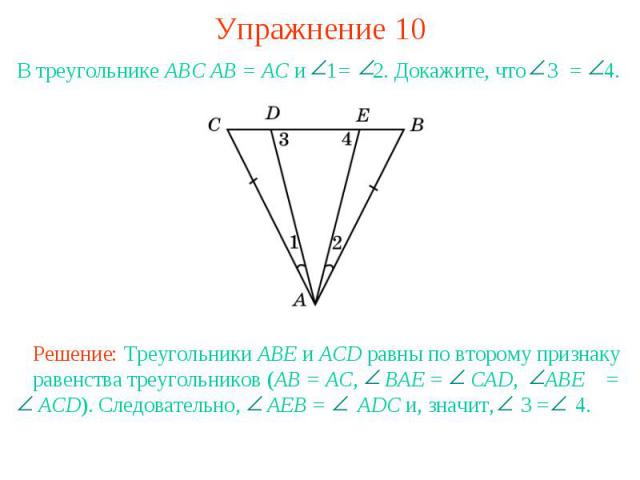
Упражнение 10В треугольнике АВС АВ = АС и 1= 2. Докажите, что 3 = 4.Решение: Треугольники ABE и ACD равны по второму признаку равенства треугольников (AB = AC, BAE = CAD, ABE = ACD). Следовательно, AEB = ADC и, значит, 3 = 4.
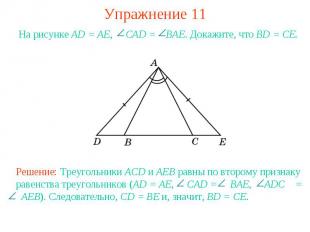
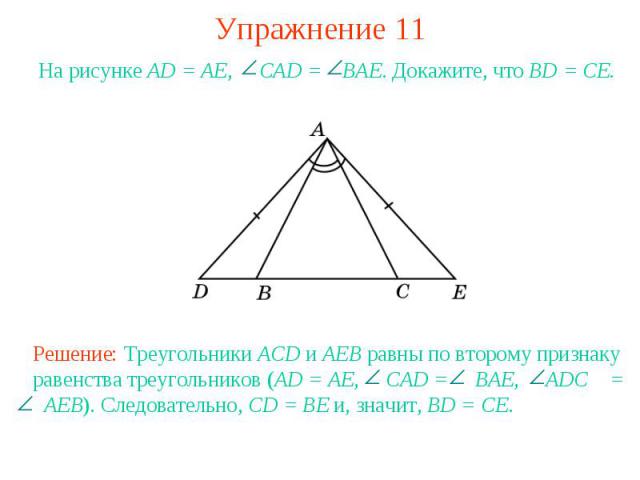
Упражнение 11На рисунке AD = AE, CAD = BAE. Докажите, что BD = CE.Решение: Треугольники ACD и AEB равны по второму признаку равенства треугольников (AD = AE, CAD = BAE, ADC = AEB). Следовательно, CD = BE и, значит, BD = CE.
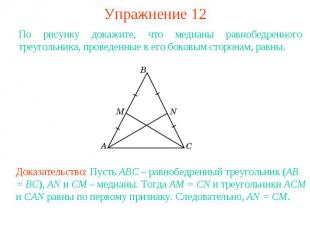
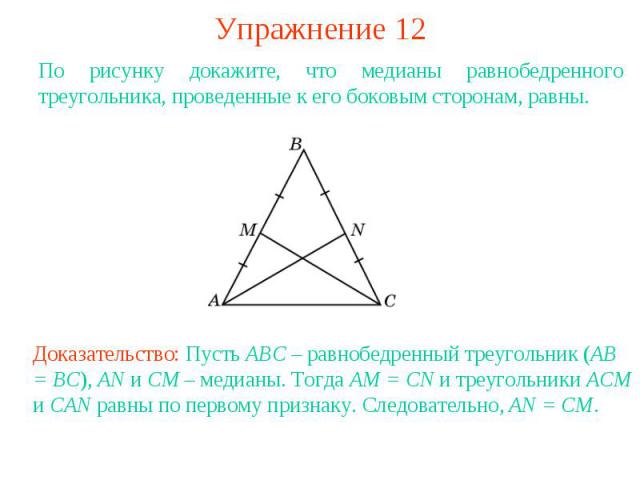
Упражнение 12По рисунку докажите, что медианы равнобедренного треугольника, проведенные к его боковым сторонам, равны.Доказательство: Пусть ABC – равнобедренный треугольник (AB = BC), AN и CM – медианы. Тогда AM = CN и треугольники ACM и CAN равны по первому признаку. Следовательно, AN = CM.
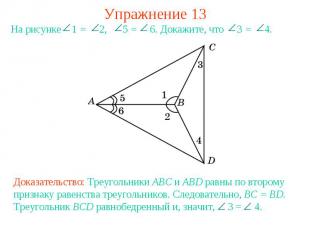
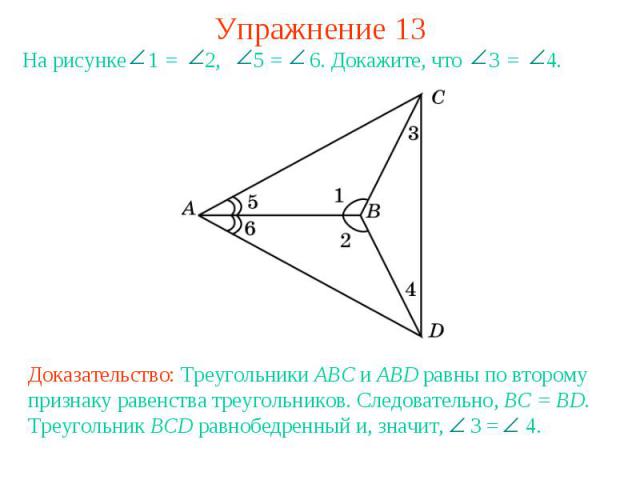
Упражнение 13На рисунке 1 = 2, 5 = 6. Докажите, что 3 = 4.Доказательство: Треугольники ABC и ABD равны по второму признаку равенства треугольников. Следовательно, BC = BD. Треугольник BCD равнобедренный и, значит, 3 = 4.
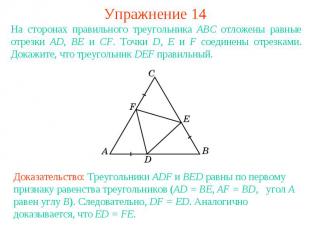
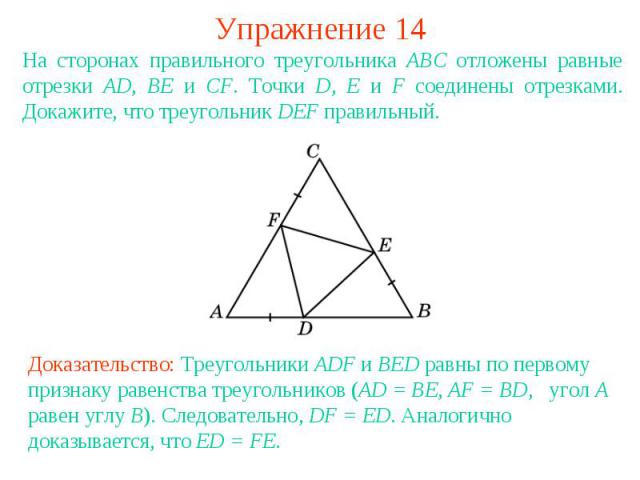
Упражнение 14На сторонах правильного треугольника АВС отложены равные отрезки AD, BE и CF. Точки D, E и F соединены отрезками. Докажите, что треугольник DEF правильный.Доказательство: Треугольники ADF и BED равны по первому признаку равенства треугольников (AD = BE, AF = BD, угол A равен углу B). Следовательно, DF = ED. Аналогично доказывается, что ED = FE.
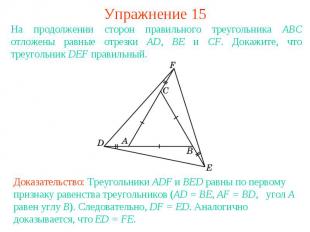
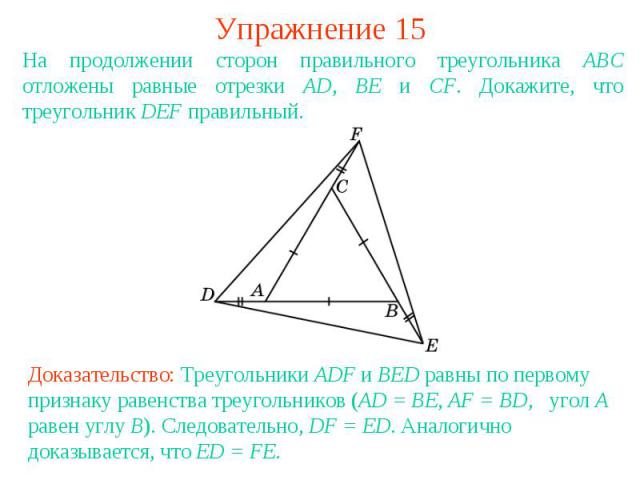
Упражнение 15На продолжении сторон правильного треугольника АВС отложены равные отрезки AD, BE и CF. Докажите, что треугольник DEF правильный.Доказательство: Треугольники ADF и BED равны по первому признаку равенства треугольников (AD = BE, AF = BD, угол A равен углу B). Следовательно, DF = ED. Аналогично доказывается, что ED = FE.