Презентация на тему: Следствия из аксиом

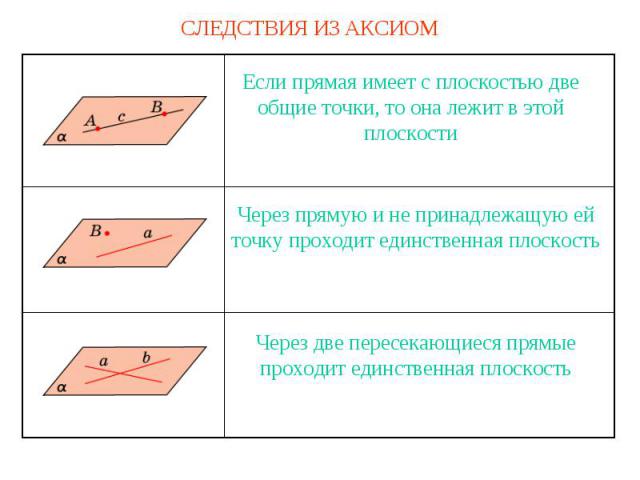
СЛЕДСТВИЯ ИЗ АКСИОМ

Упражнение 1Четыре точки не принадлежат одной плоскости. Могут ли три из них принадлежать одной прямой?

Упражнение 2Три вершины параллелограмма принадлежат некоторой плоскости. Верно ли утверждение о том, что и четвёртая вершина этого параллелограмма принадлежит той же плоскости?

Упражнение 3Две вершины и точка пересечения диагоналей параллелограмма принадлежат одной плоскости. Верно ли утверждение о том, что и две другие вершины параллелограмма принадлежат этой плоскости?

Упражнение 4Могут ли вершины замкнутой ломаной, состоящей из трёх звеньев, не принадлежать одной плоскости?

Упражнение 5Могут ли вершины замкнутой ломаной, состоящей из четырёх звеньев, не принадлежать одной плоскости?

Упражнение 6Верно ли, что через любые две прямые проходит плоскость?

Упражнение 7Прямые a, b, c попарно пересекаются. Верно ли, что они лежат в одной плоскости?

Упражнение 8Верно ли, что любая прямая, пересекающая каждую из двух данных пересекающихся прямых, лежит в плоскости этих прямых?

Упражнение 9Прямые a и b пересекаются в точке C. Через прямую a проходит плоскость , через прямую b – плоскость , отличная от . Как проходит линия пересечения этих плоскостей?

Упражнение 10Верно ли, что через любые две прямые проходит плоскость?

Упражнение 11Верно ли, что через три пересекающиеся прямые проходит плоскость?

Упражнение 12Сколько плоскостей можно провести через четыре точки?

Упражнение 13Сколько плоскостей можно провести через различные тройки из пяти точек, никакие четыре из которых не принадлежат одной плоскости?

Упражнение 14На сколько частей делят пространство три плоскости, имеющие одну общую точку?

Упражнение 15На какое наибольшее число частей могут делить пространство; а) одна плоскость; б) две плоскости; в) три плоскости; в) четыре плоскости?