Презентация на тему: Теорема Пифагора задачи

Теорема Пифагоразадачи

Формулировки и формулаСформулируйте и запишите с помощью букв a, b и c теорему Пифагора.Сформулируйте теорему, обратную теореме Пифагора.При решении каких задач применяются эти теоремы?
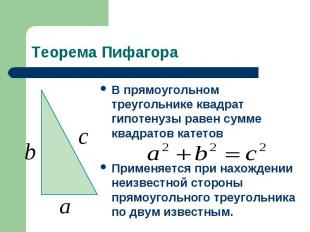
Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовПрименяется при нахождении неизвестной стороны прямоугольного треугольника по двум известным.

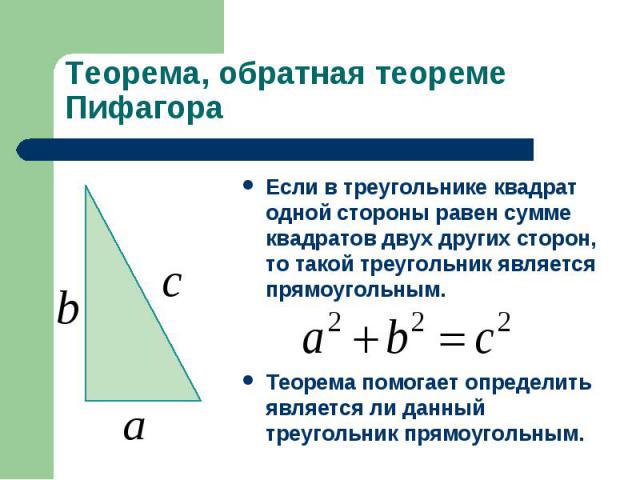
Теорема, обратная теореме ПифагораЕсли в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным.Теорема помогает определить является ли данный треугольник прямоугольным.

Задача №1В прямоугольном треугольнике катеты равны 6 см и 8 см. Чему равна гипотенуза?
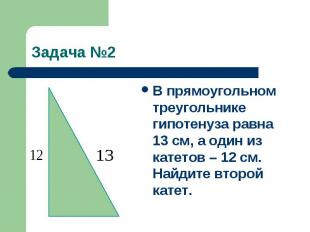
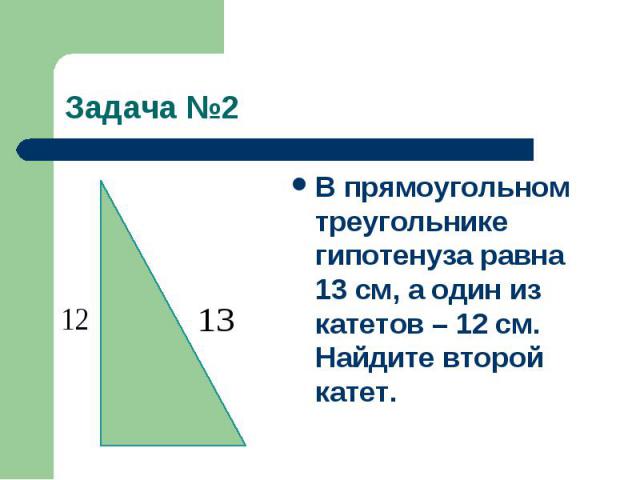
Задача №2В прямоугольном треугольнике гипотенуза равна 13 см, а один из катетов – 12 см. Найдите второй катет.

Задача №3 Определите, является ли прямоугольным треугольник со сторонами 8 м, 5 м и 9 м.

Задача №4В треугольнике две стороны равны соответственно 20 см и 15 см. Какой должна быть большая сторона, чтобы треугольник был прямоугольным?

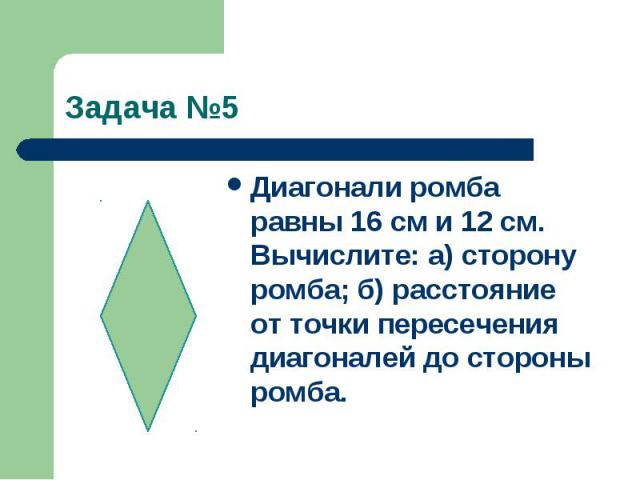
Задача №5Диагонали ромба равны 16 см и 12 см. Вычислите: а) сторону ромба; б) расстояние от точки пересечения диагоналей до стороны ромба.

Задача №6В прямоугольной трапеции большая боковая сторона и меньшая диагональ равны по 13 см, а меньшее основание 12 см. Вычислите: а) высоту трапеции; б) большую диагональ.

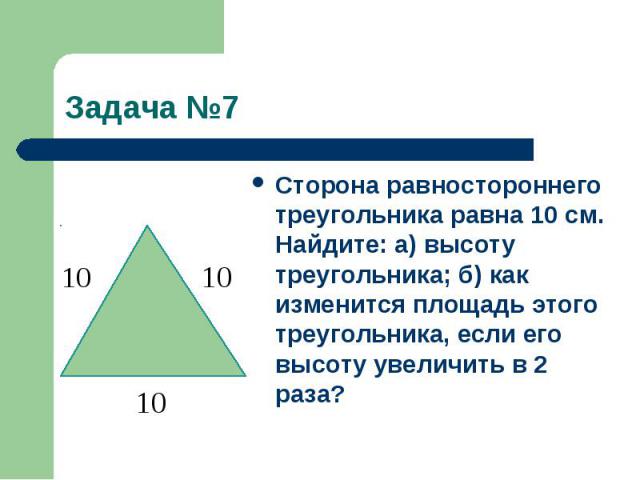
Задача №7Сторона равностороннего треугольника равна 10 см. Найдите: а) высоту треугольника; б) как изменится площадь этого треугольника, если его высоту увеличить в 2 раза?