Презентация на тему: Объем пирамиды

Объем пирамиды Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action

Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза? Найдем отношение объемов

Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды. V = SoH

Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .

Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .

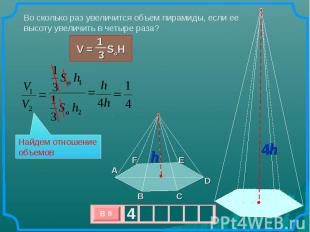
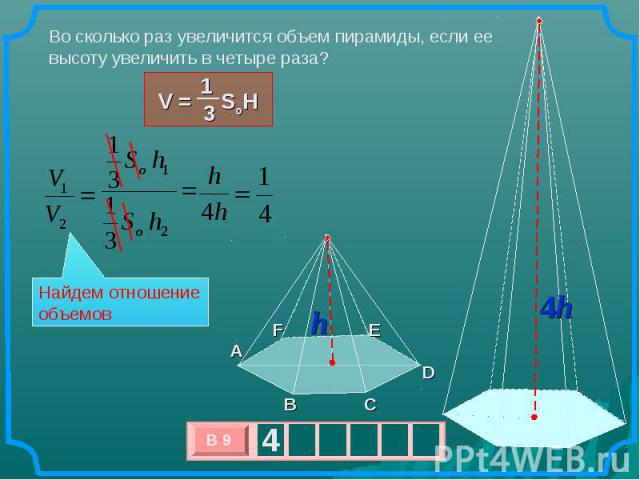
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? Найдем отношение объемов

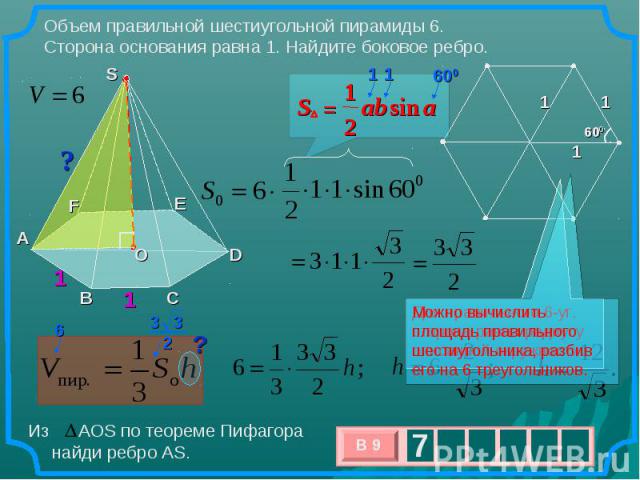
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро. Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников. Из АОS по теореме Пифагора найди ребро AS.

В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

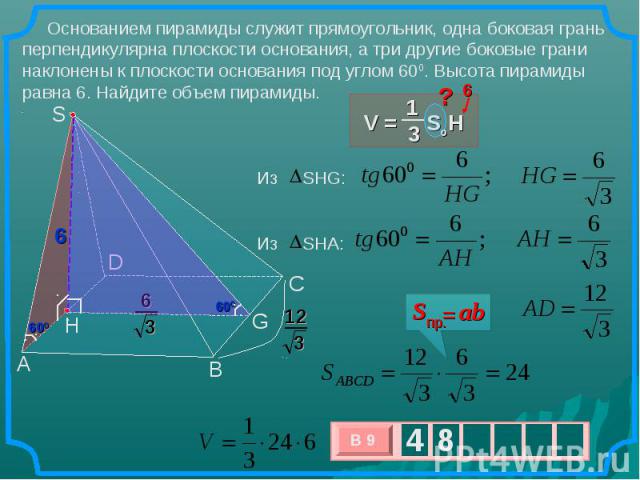
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 6. Найдите объем пирамиды.

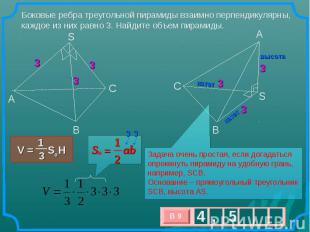
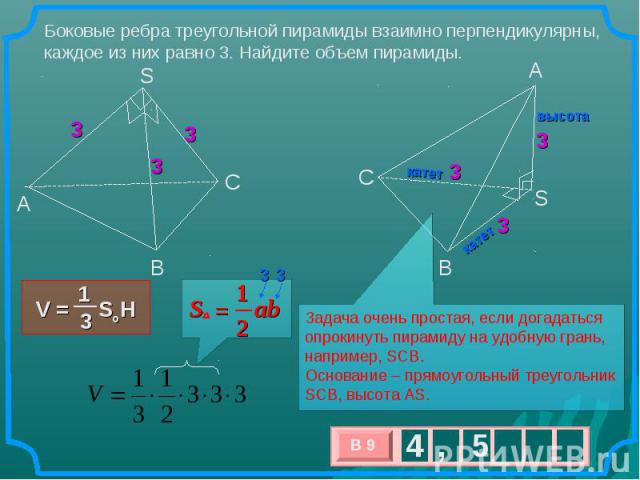
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. Задача очень простая, если догадаться опрокинуть пирамиду на удобную грань, например, SCB. Основание – прямоугольный треугольник SCB, высота AS.

Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450. Найдите объем пирамиды. Найдем ОК по теореме Пифагора Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников.

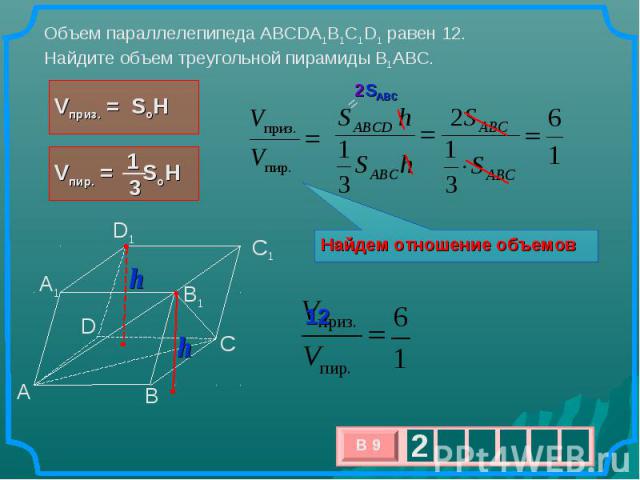
Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. Найдем отношение объемов

Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1. Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1. А объем каждой из них легко посчитать — мы делали это в предыдущей задаче. Например, найдем объем пирамиды ABCB1. Четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1 Объем пирамиды АD1CB1

Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба. Найдем отношение объемов

От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части. Найдем отношение объемов

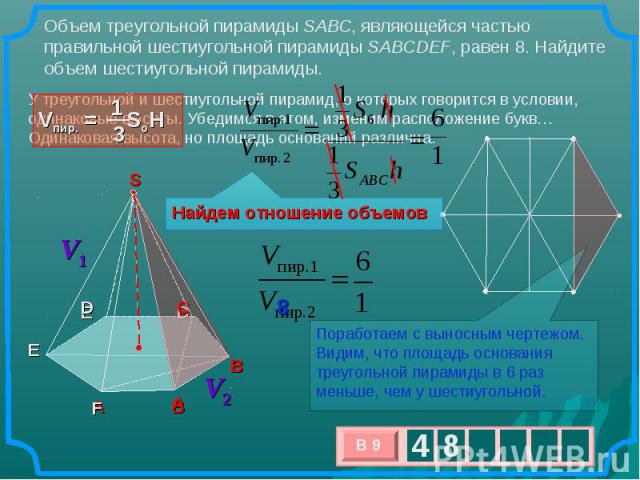
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды. У треугольной и шестиугольной пирамид, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв…Одинаковая высота, но площадь оснований различна. Поработаем с выносным чертежом. Видим, что площадь основания треугольной пирамиды в 6 раз меньше, чем у шестиугольной.

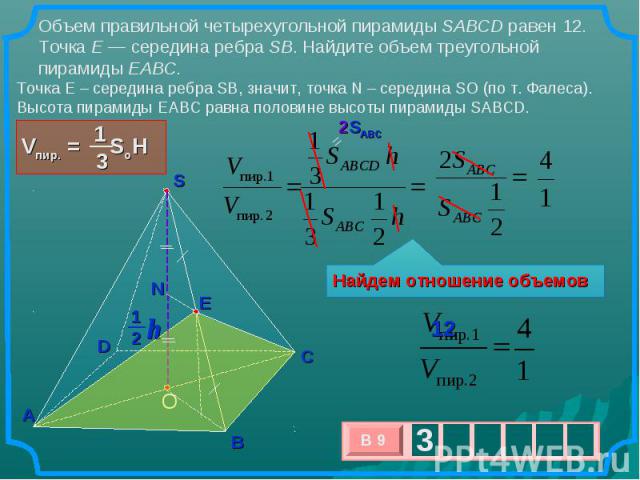
Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC. Точка E – середина ребра SB, значит, точка N – середина SO (по т. Фалеса). Высота пирамиды EABC равна половине высоты пирамиды SABCD. Найдем отношение объемов

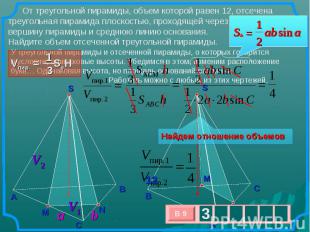
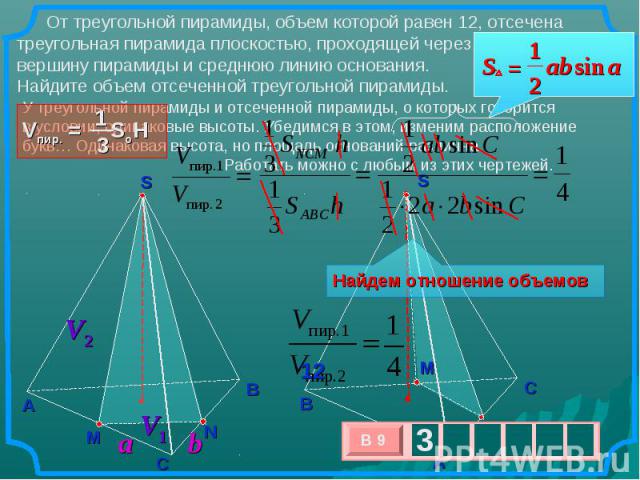
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. У треугольной пирамиды и отсеченной пирамиды, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв… Одинаковая высота, но площадь оснований различна. Работать можно с любым из этих чертежей. Найдем отношение объемов

Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. Найдем объем пирамиды NABC. Сравним его с объемом всей пирамиды SABC, составив отношение.Основания у них одинаковые – треугольник АВС.А высоты разные, сравним их.