Презентация на тему: ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ

ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕОБЪЕМ ПИРАМИДЫПрезентация выполнена учителем математикиМОУ «СОШ№6» п ПередовогоБогдановской В.М.

Необходимые формулы и теоремыПлощадь треугольника можно вычислить по формуламПлощадь прямоугольного треугольника можно вычислить по формулеОбъем пирамиды V=1/3SоснHМедианы в треугольнике точкой пересечения делятся в отношении 2:1 начиная от вершиныПлощадь квадрата или ромба S=1/2d1d2.Площадь ромба, параллелограмма S=ahРадиус окружности описанной около треугольника можно вычислить по формуле Центр окружности,описанной около прямоугольного треугольника, расположен в середине гипотенузы

Дано: DABC- правильная пирамидаАВ=3, AD=23Найти:VРешение:1. Учтите, что в основании равносторонний треугольник.Найдите площадь основания.2. Из треугольника АМС найдите медиану МС.3. Вспомните свойство точки пересечения медиан. Найдите длину АС.4. Из треугольника DOC найдите высоту пирамиды DO.5. Найдите объем пирамиды.Предложите свое решение.

Дано: FABCD- правильная пирамидаFCO=45º, FO=2Найти: VРешение:1.Определите вид треугольника FOC и его углы.Сделайте вывод о длине ОС.2. Найдите АС.3.Вспомните формулу для нахождения площади квадрата по его диагоналям.Найдите площадь основания.4.Вычислите объем пирамиды. Предложите свое решение.

Дано:FABCDEK-правильная пирамида,FO(ABC),FМAK, FO=4, FM=5Решение:1. Из треугольника FOM найдите МО2. Из треугольника МОК наудите МК, обозначив МК=х, используя для составления уравнения известную теорему.3. Найдите площадь равностороннего треугольника АОК4.Найдите площадь основания , которая состоит из площадей равных треугольников5. Вычислите объем пирамиды. Предложите свое решение.

№4Дано: DABC- пирамида,треугольник АВС прямоугольный,АВ-гипотенуза АС=6, ВС=8.Каждое боковое ребро составляет с плоскостью основания угол 45оНайти: VРешение:1.Найдите площадь прямоугольного треугольника АВС по известным катетам. 2 Вспомните,где расположен центр окружности,описанной около прямоугольного треугольника АВС..3.Из прямоугольного треугольника АВС найдите гипотенузу АВ,ОВ. 4..Определите вид треугольника DOB и его углы.Сделайте вывод о длине ОD.5.Вычислите объем пирамиды.Предложите свое решение

№5Дано: DABC- пирамида, треугольник АВС равнобедренный АС=АВ=10, ВС=12. AD=BD=CD=5Найти:VРешение:1. Из треугольника АСМ найдите медиану АМ2. АМ- высота, найдите площадь треугольника АСМ.3.Исходя из условия AD=BD=CD, О-центр описанной окружности.Найдите R=ОМ из соответствующей формулы.4. Из прямоугольного треугольника АОD найдите катет DO (высоту пирамиды)5.Вычислите объем пирамидыПредложите свое решение

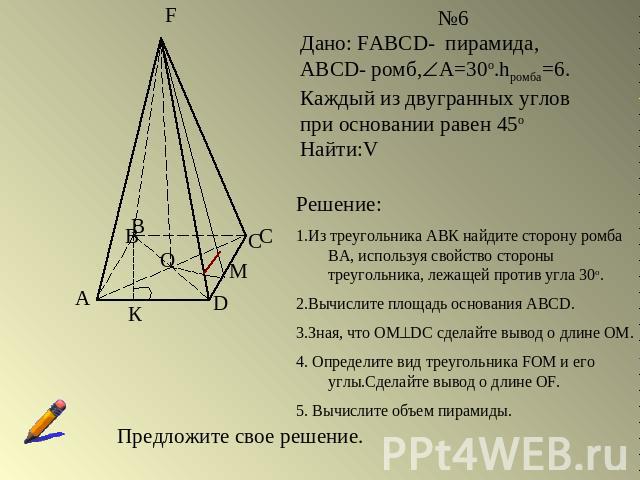
№6Дано: FABCD- пирамида, ABCD- ромб,А=30о.hромба=6. Каждый из двугранных углов при основании равен 45оНайти:VРешение:1.Из треугольника АВК найдите сторону ромба ВА, используя свойство стороны треугольника, лежащей против угла 30о.2.Вычислите площадь основания АВСD.3.Зная, что ОМDC сделайте вывод о длине ОМ.4. Определите вид треугольника FOМ и его углы.Сделайте вывод о длине ОF.5. Вычислите объем пирамиды.Предложите свое решение.

№7Дано: DABC- пирамида треугольник АВС равнобедренный АС=АВ=10, ВС=12. Каждый из двугранных углов при основании равен 45оНайти:VРешение: 1. Из треугольника АСМ найдите медиану АМ2. АМ- высота, найдите площадь треугольника АСМ.3. . Вспомните свойство точки пересечения медиан. Найдите длину ОМ.4. Определите вид треугольника DOМ и его углы.Сделайте вывод о длине ОD.5. Вычислите объем пирамидыПредложите свое решение

ЖЕЛАЮ УДАЧИ