Презентация на тему: Объём. Цилиндр, призма

Объём. Цилиндр, призма Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action

В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см3. Объем детали будет равен объему вытесненной жидкости – это известно нам из курса физики. Найдем отношение объемов

В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого? Ответ выразите в сантиметрах. Найдем отношение объемов Объем жидкости не изменился, т.е. V1=V2

В сосуд, имеющий форму правильной треугольной призмы, налили 1500 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали. Ответ выразите в см3. Объем детали будет равен объему вытесненной жидкости – это известно нам из курса физики. Найдем отношение объемов

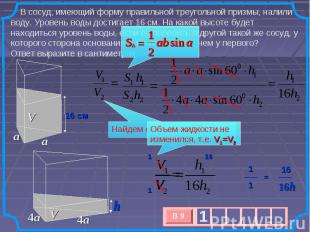
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах. Объем жидкости не изменился, т.е. V1=V2 Найдем отношение объемов

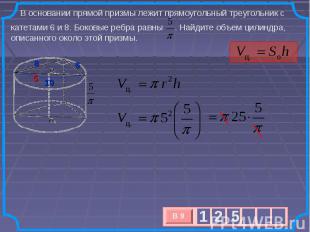
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах. Найдем отношение объемов

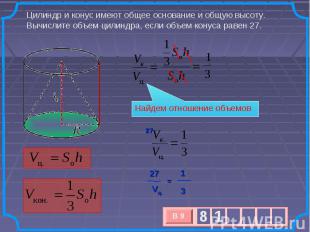
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27. Найдем отношение объемов

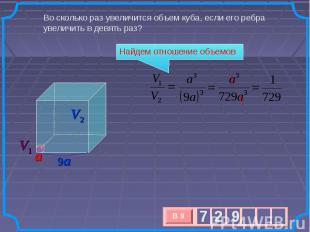
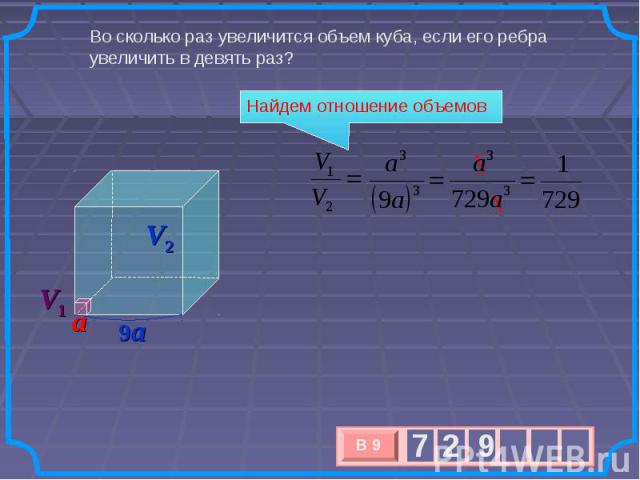
Во сколько раз увеличится объем куба, если его ребра увеличить в девять раз? Найдем отношение объемов

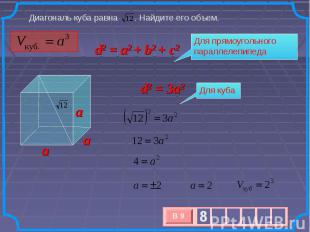
Диагональ куба равна . Найдите его объем. d2 = a2 + b2 + c2 Для прямоугольного параллелепипеда Для куба

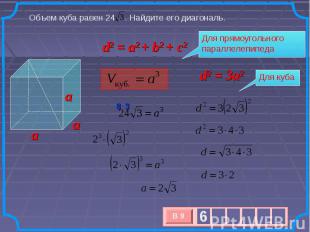
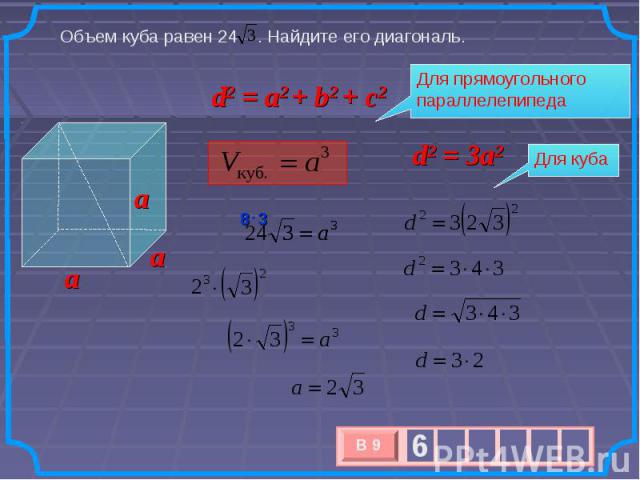
Объем куба равен 24 . Найдите его диагональ. Для прямоугольного параллелепипеда d2 = a2 + b2 + c2 Для куба

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. d2 = a2 + b2 + c2 Для прямоугольного параллелепипеда

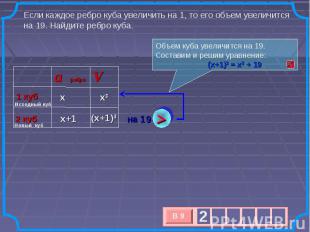
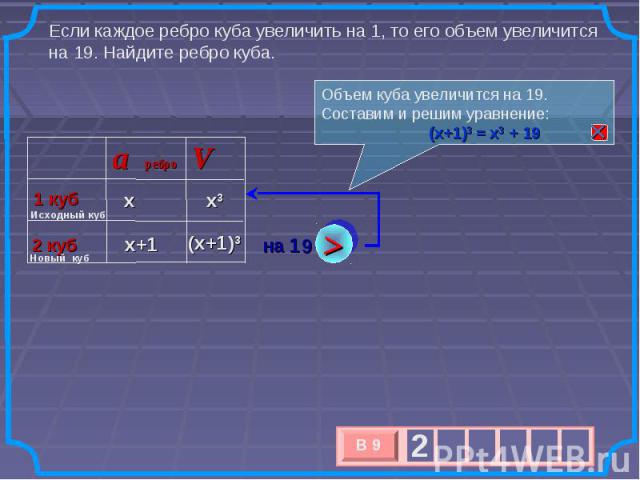
Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. Объем куба увеличится на 19. Составим и решим уравнение: (х+1)3 = х3 + 19

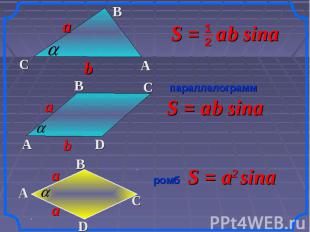
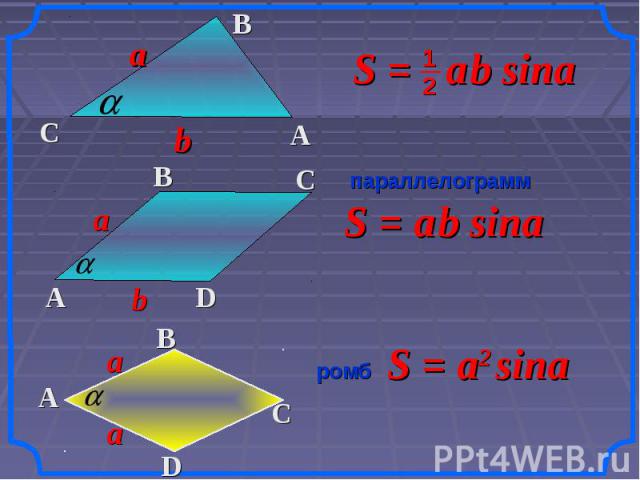
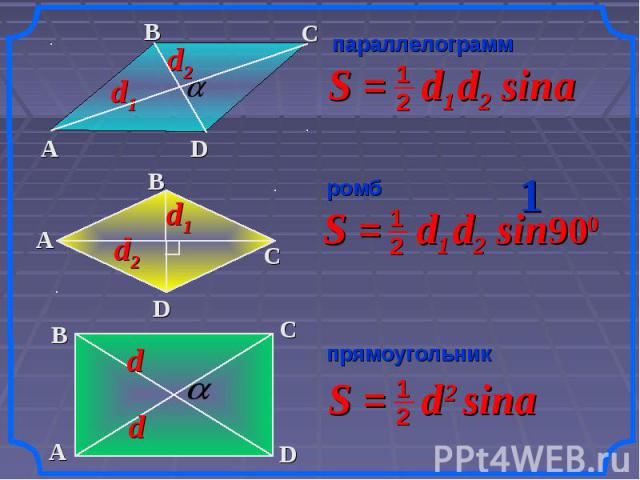
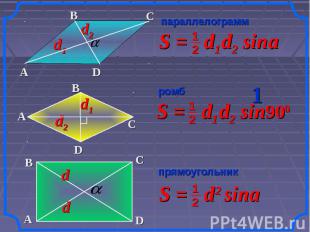
параллелограмм ромб прямоугольник

Найдите объем правильной шестиугольной призмы, стороны основания которой равны 9, а боковые ребра равны . Например, можно вычислить площадь правильного 6-уг., разбив его на 6 треугольников.

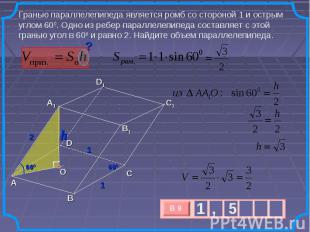
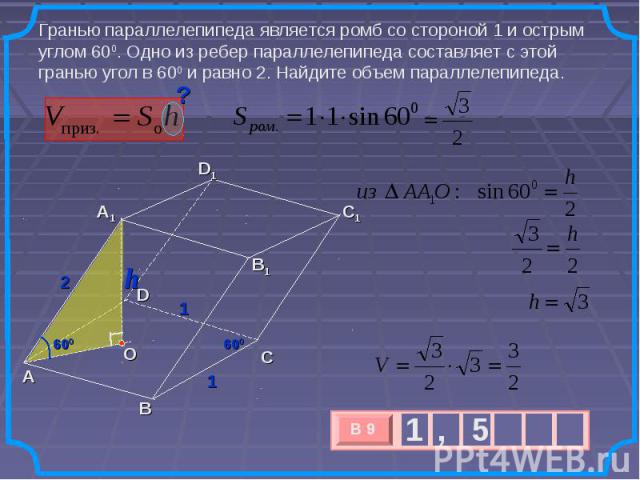
Гранью параллелепипеда является ромб со стороной 1 и острым углом 600. Одно из ребер параллелепипеда составляет с этой гранью угол в 600 и равно 2. Найдите объем параллелепипеда.

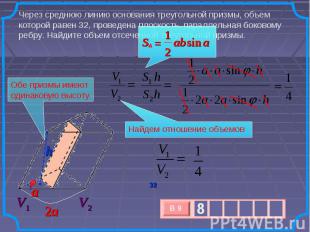
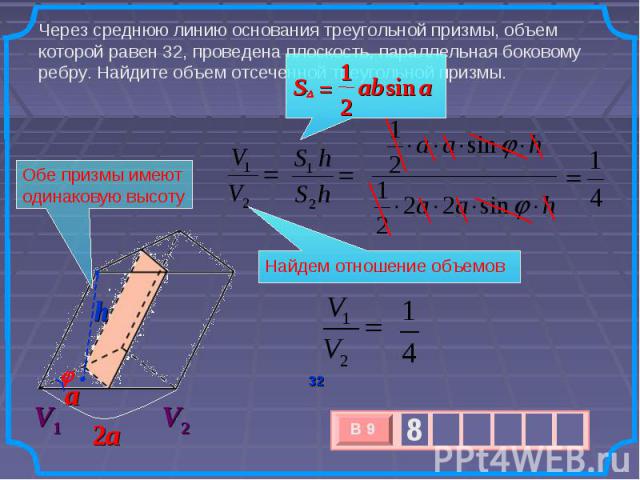
Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. Обе призмы имеют одинаковую высоту Найдем отношение объемов

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы. Применим результат, полученный в предыдущей задаче

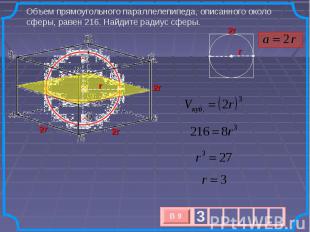
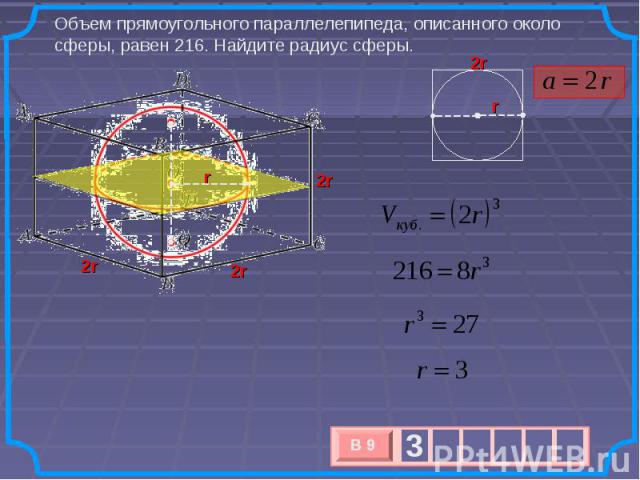
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2  и наклонены к плоскости основания под углом 300. Например, можно вычислить площадь правильного 6-уг., разбив его на 6 треугольников.

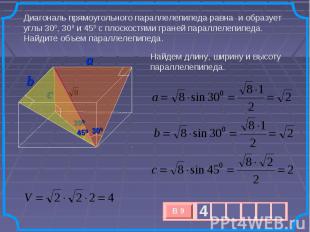
Диагональ прямоугольного параллелепипеда равна и образует углы 300, 300 и 450 с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.                        Найдем длину, ширину и высоту параллелепипеда.                     

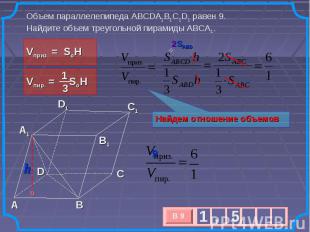
Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABCA1.                     Найдем отношение объемов