Презентация на тему: Фигуры вращения

Фигуры вращения

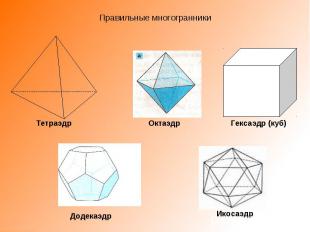
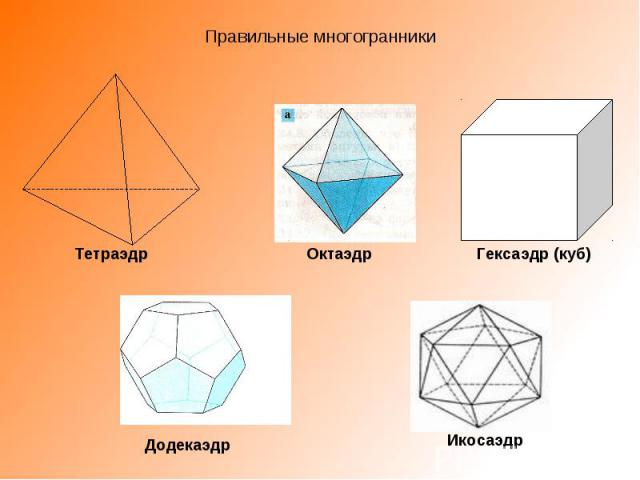
Правильные многогранники

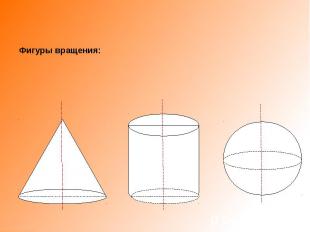
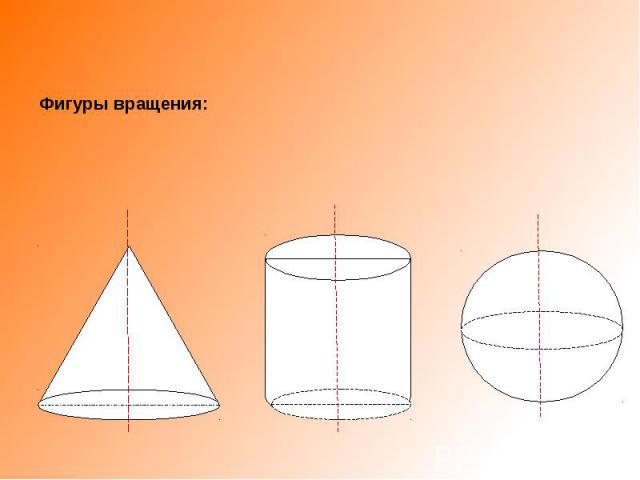
Фигуры вращения:

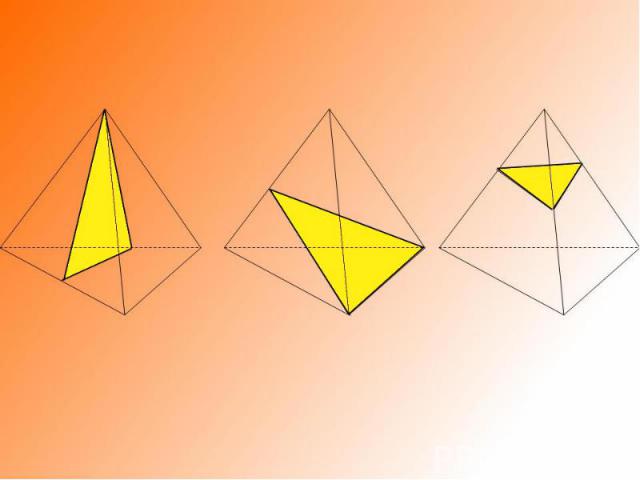
• при вращении тетраэдра в зависимости от оси вращения, получается конус, два разных конуса с общим основанием, однополостный гиперболоид;• при вращении куба: цилиндр, однополостный гиперболоид, система из двух конусов и однополостного гиперболоида;

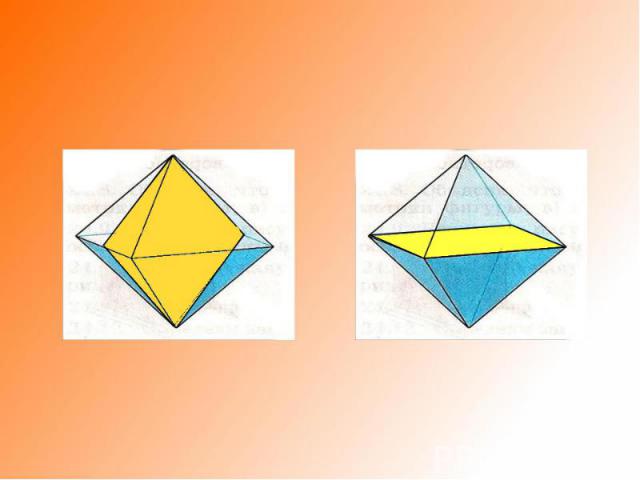
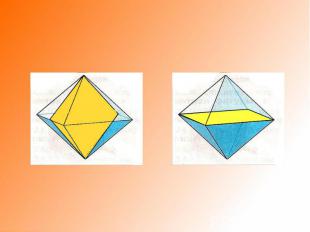
• при вращении октаэдра: два конуса с общим основанием, однополостный гиперболоид, система из двух цилиндров и двух однополостных гиперболоидов;• при вращении икосаэдра: система из двух усеченных конусов и однополостного гиперболоида, система из двух конусов и однополостного гиперболоида,система из двух плоских кругов (сверху и снизу), трех гиперболоидов и системы цилиндров;

• при вращении додекаэдра: совокупность системы однополостных гиперболоидов вращения с однополостным гиперболоидом и системой конусов, система их двух усеченных конусов и однополостного гиперболоида, система из четырех пар однополостных гиперболоидов и одной пары цилиндров.

Если прямая параллельна оси вращения, то получается цилиндрическая поверхность.Если прямая пересекает ось вращения, то получается коническая поверхность.Если прямая скрещивается с осью вращения, то получается однополостный гиперболоид вращения.

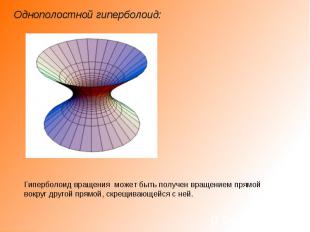
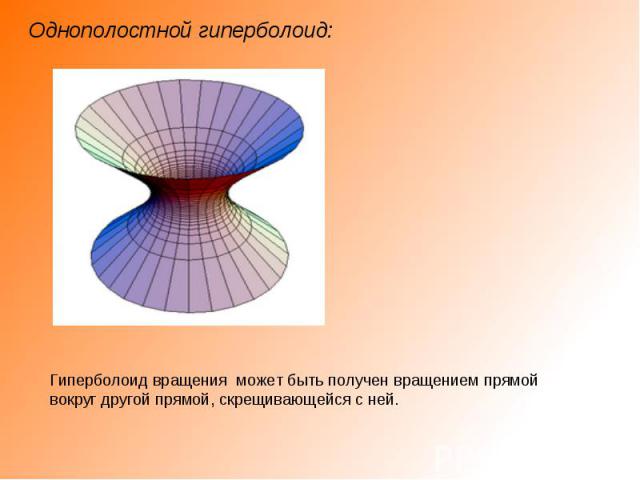
Однополостной гиперболоид: Гиперболоид вращения может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

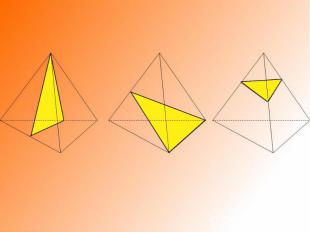
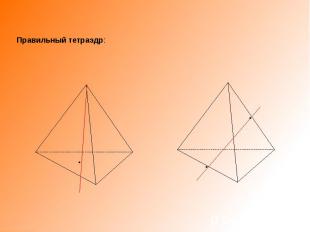
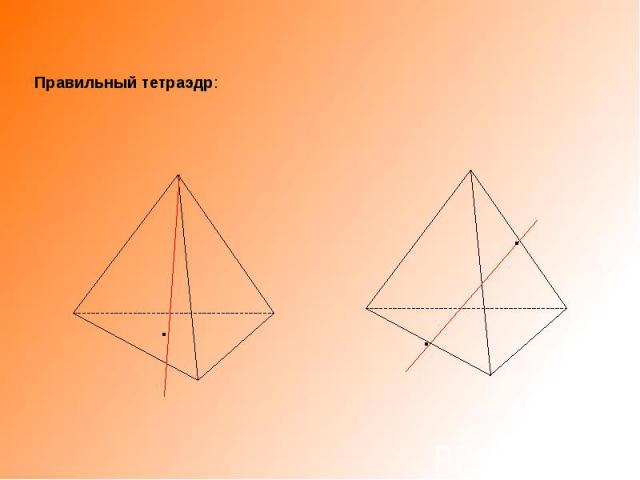
Правильный тетраэдр:

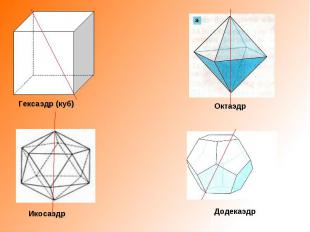
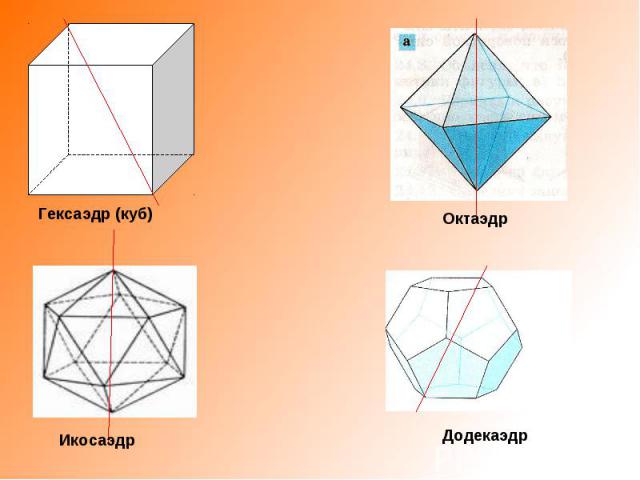
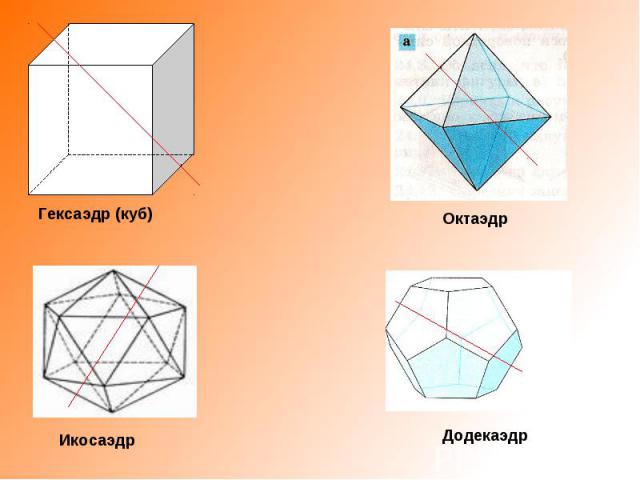
Гексаэдр (куб) Октаэдр Икосаэдр Додекаэдр

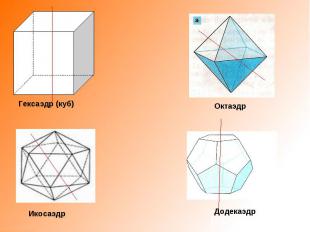
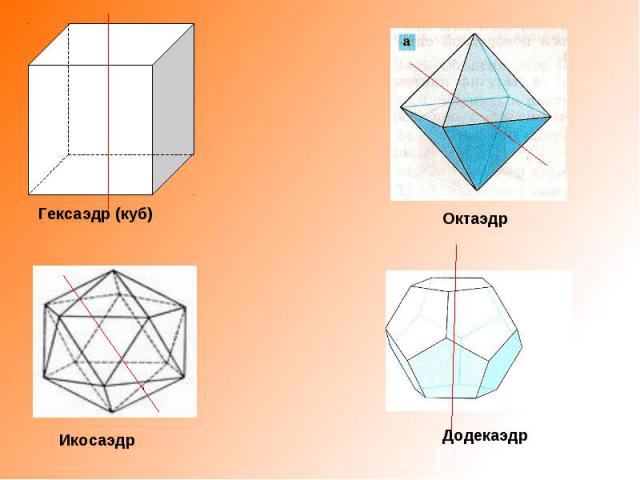
Гексаэдр (куб) Октаэдр Икосаэдр Додекаэдр

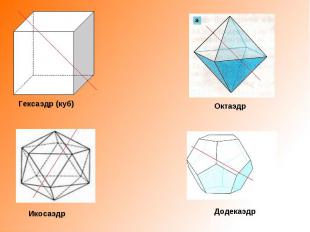
Гексаэдр (куб) Октаэдр Икосаэдр Додекаэдр

При вращении Платоновых тел, вращая разные многогранники, можно получить одинаковые фигуры вращения:• при вращении тетраэдра и октаэдра фигурой вращения являются однополостный гиперболоид а также два конуса с общим основанием;• при вращении икосаэдра и додекаэдра – система из двух усеченных конусов и однополостного гиперболоида; • при вращении икосаэдра и куба - система из двух конусов и однополостного гиперболоида.

Спасибо за внимание!